Polynomisk minsta kvadratregression i Excel
Det finns tillfällen då det inte räcker med en linje som passar bäst (dvs. ett polynom av första ordningen). Kalibreringsdata som är uppenbart krökta kan ofta anpassas på ett tillfredsställande sätt med ett polynom av andra (eller högre) ordning. Kalibreringskurvor vid atomabsorption är ofta något krökta; här är ett exempel från en annan handledning.
Exempel
Du vill analysera blykoncentrationen i kranvatten med hjälp av grafitugn-AAS. Följande data har samlats in. Rapportera koncentrationen av bly i kranvattnet i form av ett konfidensintervall.
| Blykoncentration, ppb | signal, A-s |
|---|---|
| blank | 0.006 |
| 10.0 | 0.077 |
| 20.0 | 0.138 |
| 30.0 | 0.199 |
| 40.0 | 0.253 |
| 50.0 | 0,309 |
| 60,0 | 0,356 |
| Tappvattenprov | 0,278 |
Först måste uppgifterna föras in i ett Excel-arbetsblad (klicka på bilden för att ladda ner filen).
Ett sätt att utföra polynomial regression är att anpassa lämplig trendlinje till data (och det finns ett antal alternativ utöver polynom). Resultatet visas i följande skärmdump.
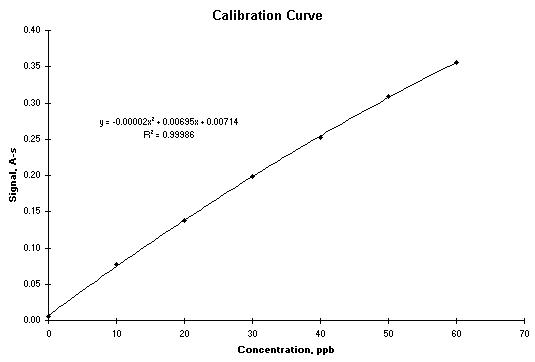
 |
Se hur detta görs. |
Och även om ovanstående tillvägagångssätt är användbart när det gäller att ge ytterligare information på en kalibreringsdiagramm, så saknas en del information (t.ex. standardfelet i skattningarna eller standardavvikelsen i residualerna). Det är möjligt att använda tilläggsmodulen Analysis ToolPak för att få denna information. Först måste du skapa en annan kolumn vars celler innehåller de kvadrerade koncentrationsvärdena.
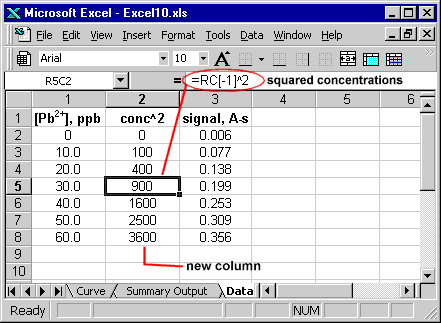
Nu kan du åberopa tilläggsmodulen Analysis TookPak. När du väljer X-området markerar du det block som innehåller både koncentrationerna och deras kvadrerade värden.
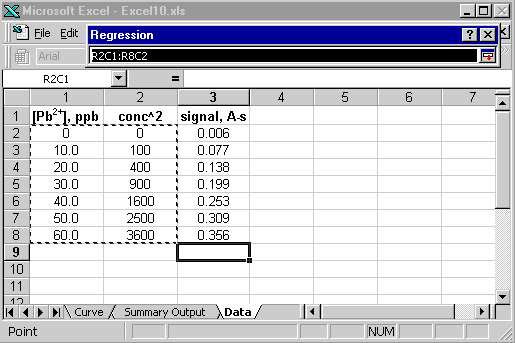
Dialogrutan för regression bör alltså se ut så här:
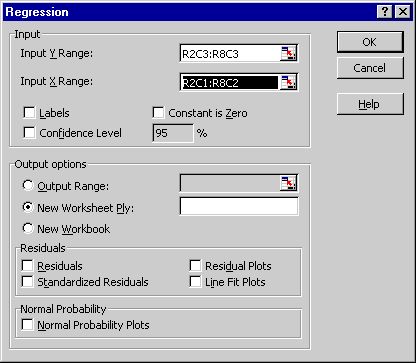
Resultatet från regressionsmodulen visas nedan. Klicka på bilden för att ladda ner Excel-filen.
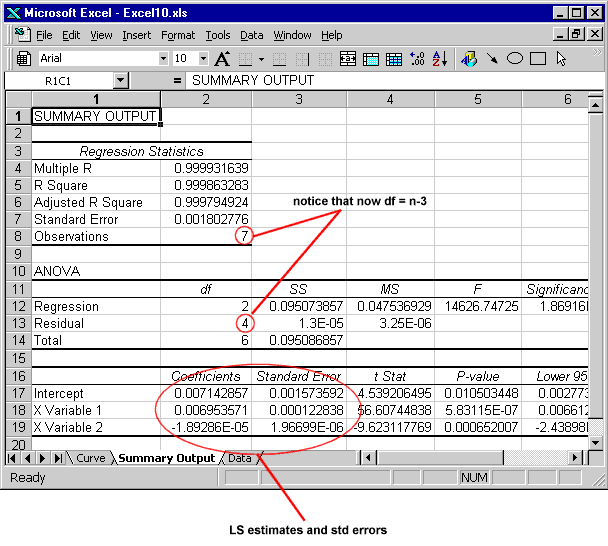
 |
Se en demonstration av hur Analysis ToolPak används för att utföra andra ordningens polynomialregression |
.