 Gästinlägg av Kady Dupre
Gästinlägg av Kady Dupre
Här är ett ordproblem för dig:
Miss Friday’s klass gör ett dagligt ordproblem. Tio av hennes elever är duktiga på ordproblem som rör addition, och endast sju verkar förstå ordproblem som rör subtraktion. Fem av hennes elever är uttråkade av de lätta problemen. Tretton elever kämpar fortfarande med grundläggande matematiska fakta och tre har svårt att läsa ordproblemen överhuvudtaget. Hur många av hennes elever är engagerade och lär sig?
Här kommer en bättre fråga: ”
Varför eleverna kämpar med matematiska ordproblem
Elverna kämpar med matematiska ordproblem av många anledningar, men tre av de största som jag har stött på är:
Problem nr 1: Elevernas självförtroende
För många elever leder det till ångest bara att titta på ett ordproblem. Ingen kan tänka klart med en känsla av rädsla eller rädsla för att misslyckas!
Syfte nr 2: Flexibelt tänkande
Många barn får lära sig att lösa ordproblem på ett metodiskt sätt, med en föreskrivande steg-för-steg-plan där man använder nyckelord som inte alltid fungerar. Planer är bra, men inte när eleverna använder dem som en krycka snarare än ett verktyg. Dagens standardiserade prov och tillämpningar i den verkliga världen kräver kreativt tänkande och flexibilitet med strategier.
Fråga nr 3: Differentiering
Lärare vill att eleverna ska prestera snabbt och trycker ofta på för snabbt, för tidigt. När det gäller ordproblem måste man gå långsamt för att gå snabbt. Precis som i guidad läsning vill du ge mycket övning med ”lagom” problem och ge guidad övning med problem som ligger precis över elevernas nivå.
3 Problemlösningsstrategier
Lösningen är att erövra matematiska ordproblem med engagerande klassrumsstrategier som motverkar ovanstående problem!
1. Lär ut en rutin för problemlösning
Barn (och vuxna) är notoriskt impulsiva problemlösare. Många elever ser ett ordproblem och vill genast rycka fram siffrorna och ”göra något” med dem. När jag gick i grundskolan var detta faktiskt en ganska pålitlig strategi! Men i dag ombeds barnen att lösa mycket mer komplexa problem, ofta med knepiga formuleringar eller avsiktliga distraktorer.
Groda flexibla tänkare och bygga upp självförtroende genom att lära ut en rutin. En rutin för problemlösning uppmuntrar helt enkelt eleverna att sakta ner och tänka efter före och efter lösningen. Jag har sett många effektiva rutiner, men mina favoriter innehåller alltid ett ”före, under och efter”-tänkande.
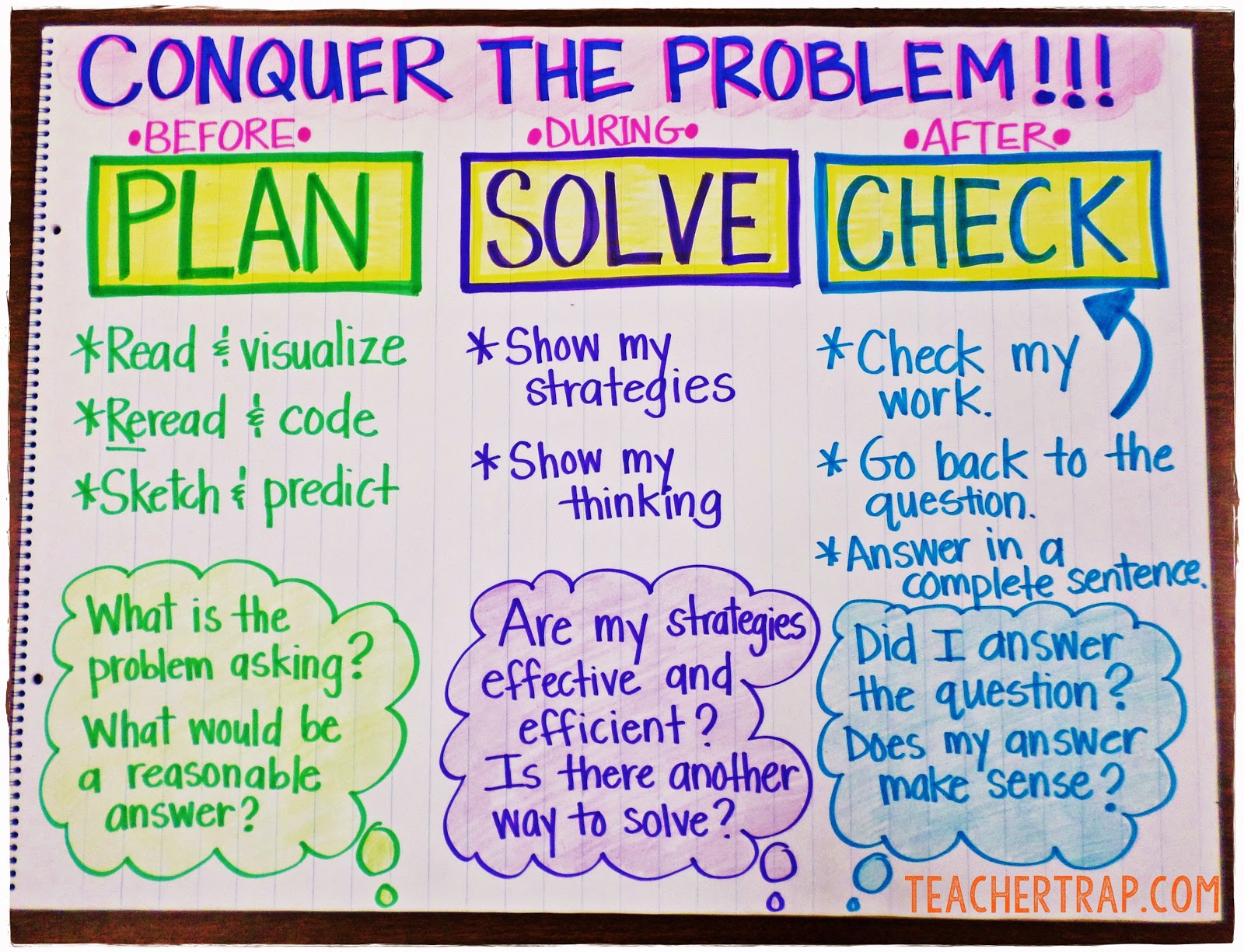
För att göra problemlösningsrutinen meningsfull och effektiv:
- Använd den ofta (om möjligt dagligen)
- Incorporera ”Turn & Teach” (Eleverna förklarar muntligt sina tankar och sin process för en partner.)
- Gör det möjligt för ”Strategy Share” efter lösningen (Utvalda elever förklarar sin metod och sitt tänkande.)

2. Differentiera ordproblem
Nej, detta betyder inte att man ska skriva ett annat ordproblem för varje elev! Det kan vara så enkelt som att justera siffrorna i ett problem eller ta bort distraktorer för elever med svårigheter. Genom att ställa upp ordproblem ökar självförtroendet och förbättrar problemlösningsförmågan genom att successivt öka svårighetsgraden i takt med att barnet är redo. Detta är särskilt effektivt när du försöker lära eleverna olika strukturer av ordproblem som passar till en viss operation.
Till exempel är jämförelse-subtraktionsproblem mycket utmanande för vissa elever. Genom att börja med en enkel version låter du eleverna fokusera på själva problemet i stället för att bli skrämda eller frustrerade.

Jag har haft stor framgång med att använda ställda problem med mina guidade mattegrupper. Efter att ha löst det enklare problemet inser eleverna att det inte är så svårt och är redo att ta sig an de svårare!
3. Jämför problem sida vid sida
För att utveckla ett flexibelt tänkande finns det inget mer kraftfullt än att analysera och jämföra ordproblem. Börja med att använda problem som har liknande berättelser och siffror, men olika problemstrukturer. Uppmuntra till samtal, använd visuella representationer och låt eleverna förklara skillnaden i struktur och funktion. Här är ett exempel som visar elevernas arbete med två liknande problem om apor. Klicka här för att ladda ner en tom kopia av dessa problem. Min gratisprodukt innehåller flera varianter som hjälper dig att differentiera.

Använd dessa tre strategier för att få barnen att tänka och prata om sina problemlösningsstrategier samtidigt som du bygger upp det ”ack så viktiga” självförtroendet, och du KAN besegra matematiska ordproblem!
