Wprowadzenie
W informatyce, skierowany graf acykliczny (DAG) jest skierowanym grafem bez cykli. W tym poradniku pokażemy, jak wykonać sortowanie topologiczne na DAG w czasie liniowym.
Sortowanie topologiczne
W wielu zastosowaniach używamy skierowanych grafów acyklicznych do wskazywania pierwszeństwa między zdarzeniami. Na przykład, w problemie harmonogramowania, istnieje zbiór zadań i zbiór ograniczeń określających kolejność tych zadań. Możemy skonstruować DAG, aby reprezentować zadania. Skierowane krawędzie DAG reprezentują kolejność zadań.
Rozważmy problem z tym, jak człowiek może się ubrać na oficjalną okazję. Musimy założyć kilka ubrań, takich jak skarpetki, spodnie, buty, itp. Niektóre ubrania muszą być założone przed innymi. Na przykład, skarpetki należy założyć przed butami. Niektóre ubrania mogą być założone w dowolnej kolejności, np. skarpetki i spodnie. Możemy użyć DAG do zilustrowania tego problemu:
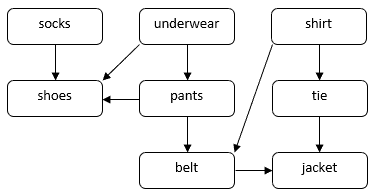
W tym DAG wierzchołki odpowiadają ubraniom. Krawędź bezpośrednia 
w DAG wskazuje, że musimy założyć ubranie 
przed ubraniem 
. Naszym zadaniem jest znalezienie kolejności zakładania wszystkich ubrań przy jednoczesnym przestrzeganiu ograniczeń zależności. Na przykład, możemy założyć ubrania w następującej kolejności:
Rozkład topologiczny DAG 
jest liniowym uporządkowaniem wszystkich jego wierzchołków w taki sposób, że jeśli zawiera krawędź , to pojawia się przed w uporządkowaniu. Dla DAG możemy skonstruować sortowanie topologiczne o czasie działania liniowym do liczby wierzchołków plus liczby krawędzi, czyli 
.
Algorytm Kahna
W DAG każda ścieżka między dwoma wierzchołkami ma skończoną długość, ponieważ graf nie zawiera cyklu. Niech 
będzie najdłuższą ścieżką z (wierzchołek źródłowy) do (wierzchołek docelowy). Ponieważ jest najdłuższą ścieżką, nie może istnieć żadna krawędź przychodząca do . Zatem DAG zawiera co najmniej jeden wierzchołek, który nie ma krawędzi przychodzącej.
3.1. Algorytm Kahna
W algorytmie Kahna konstruujemy sort topologiczny na DAG poprzez znajdowanie wierzchołków, które nie mają krawędzi przychodzących:
W tym algorytmie najpierw obliczamy wartości in-degree dla wszystkich wierzchołków.
Następnie zaczynamy od wierzchołka, którego in-degree wynosi 0 i umieszczamy go na końcu listy wyjściowej. Gdy wybierzemy wierzchołek, aktualizujemy wartości in-degree jego sąsiednich wierzchołków, ponieważ ten wierzchołek i jego zewnętrzne krawędzie są usuwane z grafu.
Powyższy proces możemy powtarzać, aż wybierzemy wszystkie wierzchołki. Lista wyjściowa jest wtedy topologicznym sortowaniem grafu.
3.2. Złożoność czasowa
Aby obliczyć stopnie wszystkich wierzchołków, musimy odwiedzić wszystkie wierzchołki i krawędzie grafu . Dlatego czas działania wynosi dla obliczeń in-degree. Aby uniknąć ponownego obliczania tych wartości, możemy użyć tablicy do śledzenia wartości stopni wewnętrznych tych wierzchołków. Wewnątrz pętli while, musimy również odwiedzić wszystkie wierzchołki i krawędzie. Dlatego całkowity czas działania wynosi .
Depth First Search
Możemy również użyć algorytmu Depth First Search (DFS) do skonstruowania sortowania topologicznego.
4.1. Graph DFS with Recursion
Zanim zajmiemy się aspektem sortowania topologicznego za pomocą DFS, zacznijmy od przeglądu standardowego, rekurencyjnego algorytmu traversal grafu DFS:
W standardowym algorytmie DFS zaczynamy od losowego wierzchołka w i oznaczamy ten wierzchołek jako odwiedzony. Następnie wywołujemy rekurencyjnie funkcję dfsRecursive, aby odwiedzić wszystkie jego nieodwiedzone sąsiednie wierzchołki. W ten sposób możemy odwiedzić wszystkie wierzchołki w czasu.
Jednakże, ponieważ umieszczamy każdy wierzchołek na liście natychmiast, gdy go odwiedzamy, i ponieważ możemy zacząć od dowolnego wierzchołka, standardowy algorytm DFS nie może zagwarantować wygenerowania topologicznie posortowanej listy.
Zobaczmy, co musimy zrobić, aby rozwiązać ten problem.
4.2. Algorytm sortowania topologicznego oparty na DFS
Możemy zmodyfikować algorytm DFS, aby wygenerować sortowanie topologiczne DAG. Podczas traversal DFS, po odwiedzeniu wszystkich sąsiadów wierzchołka , umieszczamy go na początku listy wyników 
. W ten sposób możemy mieć pewność, że wierzchołek pojawi się przed wszystkimi swoimi sąsiadami na posortowanej liście:
Algorytm ten jest podobny do standardowego algorytmu DFS. Chociaż nadal zaczynamy od losowego wierzchołka, nie umieszczamy go na liście natychmiast po jego odwiedzeniu. Zamiast tego, najpierw odwiedzamy rekurencyjnie wszystkich jego sąsiadów, a następnie umieszczamy wierzchołek na początku listy. Dlatego, jeśli zawiera krawędź , to pojawia się przed na liście.
Całkowity czas działania wynosi również , ponieważ ma taką samą złożoność czasową jak algorytm DFS.
Wniosek
W tym artykule pokazaliśmy przykład sortowania topologicznego na DAG. Omówiliśmy również dwa algorytmy, które mogą wykonać sortowanie topologiczne w czasie.
Implementacja w Javie algorytmu sortowania topologicznego opartego na DFS jest dostępna w naszym artykule na temat Depth First Search w Javie.
.