Probability > Posterior Probability & the Posterior Distribution
What is Posterior Probability?
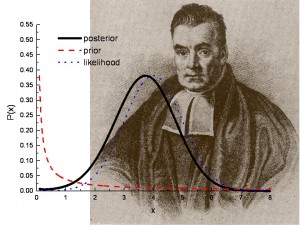
Posterior probabilities are used in Bayesian hypothesis testing. Obraz: Los Alamos National Lab.
Prawdopodobieństwo wtórne to prawdopodobieństwo, że zdarzenie będzie miało miejsce po uwzględnieniu wszystkich dowodów lub informacji tła. Jest ono blisko związane z wcześniejszym prawdopodobieństwem, które jest prawdopodobieństwem zajścia zdarzenia zanim weźmiemy pod uwagę nowe dowody. Możesz myśleć o prawdopodobieństwie potomnym jako o korekcie prawdopodobieństwa uprzedniego:
Na przykład dane historyczne sugerują, że około 60% studentów, którzy rozpoczynają studia, ukończy je w ciągu 6 lat. Takie jest wcześniejsze prawdopodobieństwo. Jednak uważasz, że liczba ta jest w rzeczywistości znacznie niższa, więc wyruszasz, aby zebrać nowe dane. Dowody, które zbierasz sugerują, że prawdziwa liczba jest w rzeczywistości bliższa 50%; To jest prawdopodobieństwo potomne.
Pochodzenie terminów
Słowa posterior i prior pochodzą od łacińskiego a priori. Definicja słowa „a priori” jest następująca:
„…odnoszące się do tego, co może być znane poprzez zrozumienie, jak pewne rzeczy działają, a nie poprzez obserwację” ~ Miriam Webster.
Przeciwieństwem „a priori” jest a posteriori, które jest definiowane jako:
„… odnoszące się do tego, co może być znane przez obserwację, a nie przez zrozumienie, jak pewne rzeczy działają” ~ Miriam Webster.
Co to jest rozkład potomny?
Rozkład potomny jest sposobem na podsumowanie tego, co wiemy o niepewnych wielkościach w analizie bayesowskiej. Jest to kombinacja rozkładu wcześniejszego i funkcji prawdopodobieństwa, która mówi, jakie informacje są zawarte w obserwowanych danych („nowe dowody”). Innymi słowy, rozkład potomny podsumowuje to, co wiemy po tym, jak dane zostały zaobserwowane. Podsumowaniem dowodów z nowych obserwacji jest funkcja prawdopodobieństwa.
Rozkłady potomne są niezwykle ważne w analizie bayesowskiej. Są one pod wieloma względami celem analizy i mogą dać ci:
- Oszacowania przedziałowe dla parametrów,
- Oszacowania punktowe dla parametrów,
- Wnioskowanie predykcyjne dla przyszłych danych,
- Oceny probabilistyczne dla twojej hipotezy.
Stephanie Glen. „Posterior Probability & the Posterior Distribution” From StatisticsHowTo.com: Elementarna statystyka dla reszty z nas! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!