- Łączność jest podstawowym pojęciem teorii grafów. Określa, czy graf jest połączony czy rozłączony. Bez łączności, nie jest możliwe, aby przejść wykres z jednego wierzchołka do innego wierzchołka.
- Grafa mówi się, że jest połączony graf, jeśli istnieje ścieżka między każdą parą wierzchołków. Od każdego wierzchołka do każdego innego wierzchołka musi istnieć jakaś ścieżka do przemierzenia. To się nazywa łączność grafu.
- Grafa mówi się, że jest rozłączony, jeśli istnieje wiele rozłączonych wierzchołków i krawędzi.
- Teorie łączności grafu są niezbędne w aplikacjach sieciowych, routingu sieci transportowych, tolerancji sieci itp.
Przykład
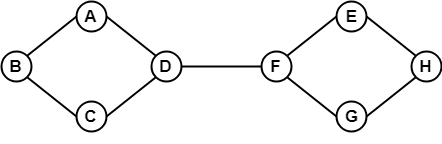
W powyższym przykładzie, możliwe jest podróżowanie z jednego wierzchołka do innego wierzchołka. W tym przypadku możemy przejść z wierzchołka B do H używając ścieżki B -> A -> D -> F -> E -> H. Stąd jest to graf połączony.
Przykład
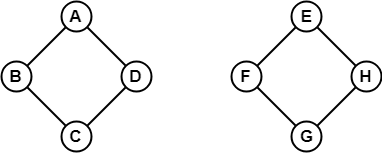
W powyższym przykładzie nie jest możliwe przejście z wierzchołka B do H, ponieważ nie ma między nimi żadnej ścieżki bezpośrednio ani pośrednio. Stąd jest to graf rozłączny.
Zobaczmy kilka podstawowych pojęć dotyczących połączoności.
Wiersz cięty
Pojedynczy wierzchołek, którego usunięcie powoduje rozłączenie grafu, nazywamy wierzchołkiem ciętym.
Pozwólmy G być grafem połączonym. Wierzchołek v w G nazywamy wierzchołkiem obciętym w G, jeśli G-v (Usuń v z G) daje w wyniku graf rozłączny.
Gdy usuniemy wierzchołek z grafu, to graf rozpadnie się na dwa lub więcej grafów. Ten wierzchołek nazywamy wierzchołkiem przeciętym.
Uwaga: Niech G będzie grafem z n wierzchołkami:
- Złączony graf G może mieć maksymalnie (n-2) wierzchołków przeciętych.
- Usunięcie wierzchołka przeciętego może pozostawić graf rozłączony.
- Usunięcie wierzchołka może zwiększyć liczbę elementów w grafie o co najmniej jeden.
- Każdy niepodlegający zawieszeniu wierzchołek drzewa jest wierzchołkiem przeciętym.
Przykład 1

Przykład 2
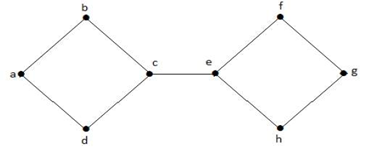
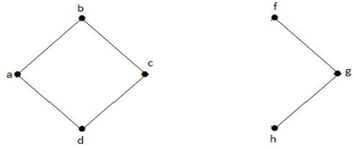
W powyższym grafie wierzchołek 'e’ jest wierzchołkiem przeciętym. Po usunięciu wierzchołka 'e’ z powyższego grafu graf stanie się grafem rozłącznym.
Wierzchnia ucięta (mostek)
Wierzchnia ucięta lub mostek to pojedyncza krawędź, której usunięcie powoduje rozłączenie grafu.
Niech G będzie grafem połączonym. Krawędź e z G nazywamy krawędzią obciętą z G, jeśli G-e (Usuń e z G) daje graf rozłączny.
Gdy usuniemy krawędź z grafu, to graf rozpadnie się na dwa lub więcej grafów. Ta usunięta krawędź jest nazywana krawędzią cięcia lub mostem.
Uwaga: Niech G będzie grafem z n wierzchołkami:
- Złączony graf G może mieć co najwyżej (n-1) krawędzi cięcia.
- Usuwanie krawędzi cięcia może pozostawić graf rozłączony.
- Usunięcie krawędzi może zwiększyć liczbę elementów w grafie co najwyżej o jeden.
- Krawędź cięcia „e” nie może być częścią żadnego cyklu w G.
- Jeśli istnieje krawędź cięcia, to musi też istnieć wierzchołek cięcia, bo co najmniej jeden wierzchołek krawędzi cięcia jest wierzchołkiem cięcia.
- Jeśli istnieje wierzchołek przecięcia, to istnienie dowolnej krawędzi przecięcia nie jest konieczne.
Przykład 1
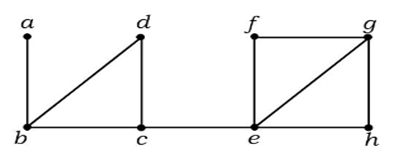
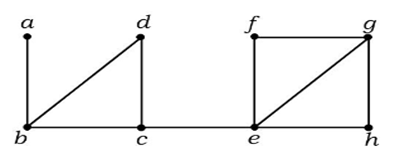
W powyższym grafie krawędź (c, e) jest krawędzią przecięcia. Po usunięciu tej krawędzi z powyższego grafu stanie się on grafem rozłącznym.
Przykład 2
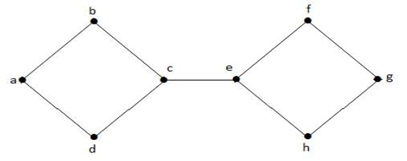
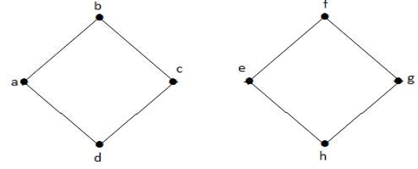
W powyższym grafie krawędź (c, e) jest krawędzią ciętą. Po usunięciu tej krawędzi z powyższego grafu graf stanie się grafem rozłącznym.
Zbiór cięty
W grafie połączonym G zbiór cięty to zbiór S krawędzi o następujących własnościach:
- Usunięcie wszystkich krawędzi w S powoduje rozłączenie G.
- Usunięcie niektórych krawędzi (ale nie wszystkich) w S nie powoduje rozłączenia G.
Przykład 1
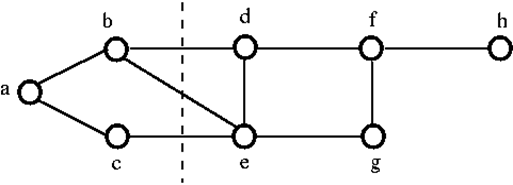
Aby rozłączyć powyższy graf G, musimy usunąć trzy krawędzie. tj. bd, be i ce. Nie możemy go rozłączyć usuwając tylko dwie z trzech krawędzi. Stąd {bd, be, ce} jest zbiorem przeciętym.
Po usunięciu zbioru przeciętego z powyższego grafu wyglądałby on następująco:
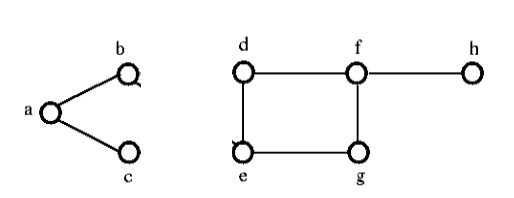
Połączalność krawędzi
Połączalność krawędzi grafu połączonego G to minimalna liczba krawędzi, których usunięcie powoduje, że G jest rozłączny. Oznaczamy ją przez λ(G).
Gdy λ(G) ≥ k, to o grafie G mówi się, że jest k-krawędziowo połączony.
Przykład
Zobaczmy przykład,
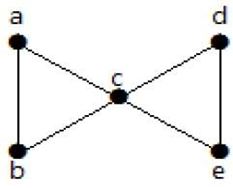
Z powyższego grafu, przez usunięcie dwóch minimalnych krawędzi, graf połączony staje się grafem rozłącznym. Stąd jego łączność krawędzi wynosi 2. Zatem powyższy graf jest grafem połączonym 2 krawędziami.
Oto cztery następujące sposoby rozłączenia grafu przez usunięcie dwóch krawędzi:
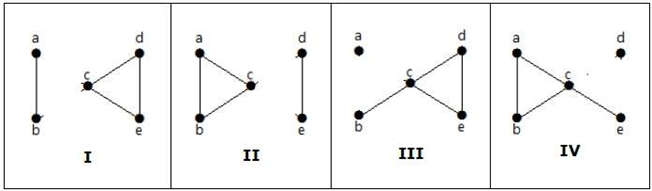
Połączalność wierzchołków
Połączalność (lub łączność wierzchołków) grafu połączonego G to minimalna liczba wierzchołków, których usunięcie powoduje, że G rozłącza się lub redukuje do grafu trywialnego. Jest ona oznaczana przez K(G).
O grafie mówimy, że jest k-związany lub k-wierzchołkowy, gdy K(G) ≥ k. Aby usunąć wierzchołek, musimy również usunąć krawędzie z nim związane.
Przykład
Zobaczmy przykład:
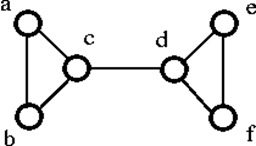
Powyższy graf G może zostać rozłączony przez usunięcie pojedynczego wierzchołka 'c’ lub 'd’. Stąd jego łączność wierzchołków wynosi 1. Jest to zatem graf 1-połączony.
.