Klasyfikacja przez analizę dyskryminacyjną
Zobaczmy jak LDA może być wyprowadzona jako nadzorowana metoda klasyfikacji. Rozważmy ogólny problem klasyfikacji: zmienna losowa X pochodzi z jednej z K klas, z pewnymi specyficznymi dla klas gęstościami prawdopodobieństwa f(x). Reguła dyskryminacyjna próbuje podzielić przestrzeń danych na K rozłącznych regionów, które reprezentują wszystkie klasy (wyobraźmy sobie pola na szachownicy). Mając te regiony, klasyfikacja za pomocą analizy dyskryminacyjnej oznacza po prostu, że przypisujemy x do klasy j, jeśli x znajduje się w regionie j. Pytanie brzmi więc, skąd wiemy, do którego regionu należą dane x? Oczywiście, możemy kierować się dwiema regułami alokacji:
- Reguła największego prawdopodobieństwa: Jeśli zakładamy, że każda klasa może wystąpić z równym prawdopodobieństwem, to przydzielamy x do klasy j, jeśli

- Reguła bayesowska: Jeśli znamy klasowe prawdopodobieństwa uprzednie, π, to przyporządkuj x do klasy j, jeśli

Liniowa i kwadratowa analiza dyskryminacyjna
Jeśli założymy, że dane pochodzą z wielowymiarowego rozkładu gaussowskiego, tzn.tzn. rozkład X może być scharakteryzowany przez jego średnią (μ) i kowariancję (Σ), można uzyskać jednoznaczne formy powyższych reguł alokacji. Zgodnie z regułą Bayesa, klasyfikujemy dane x do klasy j, jeśli ma ona największe prawdopodobieństwo spośród wszystkich K klas dla i = 1,…,K:

Powyższa funkcja nazywana jest funkcją dyskryminacyjną. Zwróćmy uwagę na użycie tutaj log-likelihood. Innymi słowy, funkcja dyskryminacyjna mówi nam, jak bardzo prawdopodobne jest, że dane x są z każdej klasy. Granica decyzyjna oddzielająca dwie klasy, k i l, jest zatem zbiorem x, w którym dwie funkcje dyskryminacyjne mają tę samą wartość. W związku z tym, wszelkie dane, które znajdują się na granicy decyzji są równie prawdopodobne z dwóch klas (nie mogliśmy zdecydować).
LDA powstaje w przypadku, gdy zakładamy równą kowariancję wśród K klas. Oznacza to, że zamiast jednej macierzy kowariancji na klasę, wszystkie klasy mają taką samą macierz kowariancji. Wówczas możemy otrzymać następującą funkcję dyskryminacyjną:

Zauważmy, że jest to funkcja liniowa w x. Zatem granica decyzyjna pomiędzy dowolną parą klas jest również funkcją liniową w x, stąd jej nazwa: liniowa analiza dyskryminacyjna. Bez założenia o równej kowariancji, człon kwadratowy w prawdopodobieństwie nie znosi się, stąd wynikowa funkcja dyskryminacyjna jest funkcją kwadratową w x:

W tym przypadku granica decyzyjna jest kwadratowa w x. Jest to znane jako kwadratowa analiza dyskryminacyjna (QDA).
Która jest lepsza? LDA czy QDA?
W rzeczywistych problemach parametry populacji są zazwyczaj nieznane i szacowane na podstawie danych treningowych jako średnie z próby i macierze kowariancji z próby. Podczas gdy QDA pozwala na bardziej elastyczne granice decyzyjne w porównaniu do LDA, liczba parametrów koniecznych do oszacowania również rośnie szybciej niż w przypadku LDA. W przypadku LDA, (p+1) parametrów jest potrzebnych do skonstruowania funkcji dyskryminacyjnej w (2). Dla problemu z K klasami, potrzebowalibyśmy tylko (K-1) takich funkcji dyskryminacyjnych poprzez arbitralny wybór jednej klasy jako klasy bazowej (odjęcie prawdopodobieństwa klasy bazowej od wszystkich innych klas). Stąd całkowita liczba szacowanych parametrów dla LDA wynosi (K-1)(p+1).
Z drugiej strony, dla każdej funkcji dyskryminacyjnej QDA w (3) należy oszacować wektor średniej, macierz kowariancji i priorytety klas:
– Średnia: p
– Kowariancja: p(p+1)/2
– Prior klasowy: 1
Podobnie, dla QDA musimy oszacować (K-1){p(p+3)/2+1} parametrów.
W związku z tym, liczba parametrów szacowanych w LDA rośnie liniowo z p, podczas gdy liczba parametrów szacowanych w QDA rośnie kwadratowo z p. Oczekiwalibyśmy, że QDA będzie miała gorszą wydajność niż LDA, gdy wymiar problemu jest duży.
Best of two worlds? Kompromis pomiędzy LDA & QDA
Możemy znaleźć kompromis pomiędzy LDA i QDA poprzez regularyzację macierzy kowariancji poszczególnych klas. Regularyzacja oznacza, że nakładamy pewne ograniczenia na szacowane parametry. W tym przypadku wymagamy, aby indywidualna macierz kowariancji kurczyła się w kierunku wspólnej połączonej macierzy kowariancji poprzez parametr kary, np. α:

Wspólna macierz kowariancji może być również regularyzowana w kierunku macierzy tożsamości poprzez parametr kary, np, β:

W sytuacjach, gdy liczba zmiennych wejściowych znacznie przekracza liczbę próbek, macierz kowariancji może być źle oszacowana. Skurcz może poprawić dokładność estymacji i klasyfikacji. Ilustruje to poniższy rysunek.

Obliczenia dla LDA
Wynika z (2) i (3), że obliczenia funkcji dyskryminacyjnych mogą być uproszczone, jeśli najpierw zdiagnozujemy macierze kowariancji. Oznacza to, że dane są przekształcane tak, aby miały identyczną macierz kowariancji (brak korelacji, wariancja równa 1). W przypadku LDA, oto jak postępujemy z obliczeniami:

Krok 2 sferyzuje dane, aby otrzymać identyczną macierz kowariancji w przekształconej przestrzeni. Krok 4 jest uzyskiwany przez podążanie za (2).
Przyjrzyjmy się przykładowi dwóch klas, aby zobaczyć, co LDA naprawdę robi. Załóżmy, że istnieją dwie klasy, k i l. Klasyfikujemy x do klasy k, jeśli

Powyższy warunek oznacza, że klasa k jest bardziej prawdopodobna do wytworzenia danych x niż klasa l. Postępując zgodnie z przedstawionymi powyżej czterema krokami, piszemy
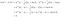
Tzn, klasyfikujemy dane x do klasy k, jeśli

Wywiedziona reguła alokacji ujawnia działanie LDA. Lewa strona (l.h.s.) równania jest długością rzutu ortogonalnego x* na odcinek linii łączącej dwie średnie klasowe. Prawa strona jest położeniem środka odcinka skorygowanego o wcześniejsze prawdopodobieństwa klasowe. Zasadniczo LDA klasyfikuje spherowane dane do najbliższej średniej klasy. Możemy tu poczynić dwie obserwacje:
- Punkt decyzyjny odchyla się od punktu środkowego, gdy wcześniejsze prawdopodobieństwa klas nie są takie same, tzn. granica jest przesuwana w kierunku klasy o mniejszym wcześniejszym prawdopodobieństwie.
- Dane są rzutowane na przestrzeń obejmowaną przez średnie klasowe (mnożenie x* i odejmowanie średniej na l.h.s. reguły). Porównania odległościowe są następnie wykonywane w tej przestrzeni.
.