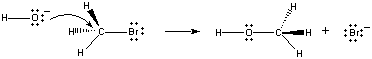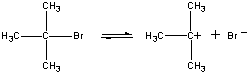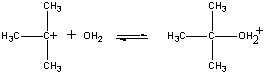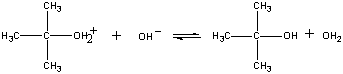Kinetyka chemiczna
Kinetyka chemiczna
Możesz być zaznajomiony z miareczkowaniem kwasowo-zasadowym, które wykorzystuje fenoloftaleinę jako wskaźnik punktu końcowego. Być może nie zauważyłeś jednak, co się dzieje, gdy roztwór zawierający fenoloftaleinę w obecności nadmiaru zasady jest pozostawiony na kilka minut. Chociaż roztwór początkowo ma różową barwę, stopniowo staje się bezbarwny, ponieważ fenoloftaleina reaguje z jonami OH- w silnie zasadowym roztworze.
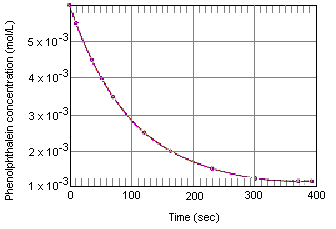
Poniższa tabela pokazuje, co dzieje się ze stężeniem fenoloftaleiny w roztworze, który początkowo miał 0,005 M fenoloftaleiny i 0,61 M jonów OH-. Jak widać, gdy dane te są wykreślone na wykresie poniżej, stężenie fenoloftaleiny zmniejsza się o współczynnik 10 w okresie około czterech minut.
Dane doświadczalne dotyczące reakcji między fenoloftaleiną a nadmiarem bazy
Doświadczenia takie jak to, które dostarczyło nam danych w powyższej tabeli, są klasyfikowane jako pomiary kinetyki chemicznej (od greckiego rdzenia oznaczającego „poruszać się”). Jednym z celów tych eksperymentów jest opisanie tempa reakcji – tempa, w którym reaktory przekształcają się w produkty reakcji.
Termin tempo jest często używany do opisania zmiany w ilościthat występuje na jednostkę czasu. Stopa inflacji, na przykład, jest zmianą średniego kosztu zbioru standardowych przedmiotów w ciągu roku. Szybkość, z jaką obiekt przemieszcza się w przestrzeni, to odległość przebyta w jednostce czasu, np. w milach na godzinę lub kilometrach na sekundę. W kinetyce chemicznej, przebyta odległość jest zmianą stężenia jednego ze składników reakcji. Szybkość reakcji jest zatem zmianą stężenia jednego z reagentów
(X)
, która zachodzi w danym okresie czasut.
Problem praktyczny 1:
Wykorzystaj dane z powyższej tabeli do obliczenia szybkości, z jaką fenoloftaleina reaguje z jonem OH- w każdym z następujących przedziałów czasu:
(a) W pierwszym przedziale czasu, gdy stężenie fenoloftaleiny spada z 0,0050 M do 0,0045 M.
(b) Podczas drugiego przedziału czasowego, gdy stężenie spada z 0,0045 M do 0,0040 M.
(c) Podczas trzeciego przedziału czasowego, gdy stężenie spada z 0,0040 M do 0,0035 M.
Kliknij tutaj, aby sprawdzić swoją odpowiedź do zadania ćwiczeniowego nr 1.
Kliknij tutaj, aby zobaczyć rozwiązanie zadania ćwiczeniowego nr 1.
Stałe szybkości reakcji i prawo szybkości dla reakcji
Szybkość reakcji między fenoloftaleiną a jonem OH- nie jest stała; zmienia się w czasie. Jak w większości reakcji, szybkość tej reakcji stopniowo maleje w miarę zużywania się reagentów. Oznacza to, że szybkość reakcji zmienia się w trakcie jej pomiaru.
Aby zminimalizować błąd, jaki wprowadza to do naszych pomiarów, wydaje się, że wskazane jest mierzenie szybkości reakcji w okresach czasu, które są krótkie w porównaniu z czasem, jaki jest potrzebny do zajścia reakcji. Możemy, na przykład, spróbować zmierzyć nieskończenie małą zmianę stężeniad(X), która zachodzi w nieskończenie krótkim okresie czasu. Stosunek tych wielkości jest znany jako chwilowa szybkość reakcji.
Rzeczowa szybkość reakcji w dowolnym momencie czasu może być obliczona z wykresu stężenia reagenta (lub produktu) w funkcji czasu. Na poniższym wykresie pokazano, jak można obliczyć szybkość reakcji rozkładu fenoloftaleiny na podstawie wykresu zależności stężenia od czasu. Szybkość reakcji w dowolnym momencie czasu jest równa nachyleniu stycznej poprowadzonej do tej krzywej w tym momencie.
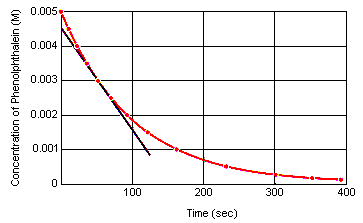
Szybkość chwilowa reakcji może być mierzona w dowolnym momencie pomiędzy momentem, w którym reagenty są mieszane, a momentem, w którym reakcja osiąga stan równowagi.Ekstrapolacja tych danych wstecz do momentu, w którym reagenty są mieszane, daje początkową szybkość chwilową reakcji.
Prawa szybkości i stałe szybkości
Ciekawy wynik otrzymuje się, gdy szybkość chwilowa reakcji jest obliczana w różnych punktach wzdłuż krzywej na wykresie w poprzedniej sekcji. Szybkość reakcji w każdym punkcie na tej krzywej jest wprost proporcjonalna do stężenia fenoloftaleiny w tym momencie czasu.
Rate = k(fenoloftaleina)
Ponieważ równanie to jest prawem doświadczalnym opisującym szybkość reakcji, nazywa się je prawem szybkości reakcji. Stała proporcjonalności, k, jest znana jako stała szybkości.
Zadanie praktyczne nr 2:
Oblicz stałą szybkości reakcji między fenoloftaleiną a jonem OH-, jeśli chwilowa szybkość reakcji wynosi 2,5 x 10-5 moli na litr na sekundę, gdy stężenie fenoloftaleiny wynosi 0,0025 M.
Kliknij tutaj, aby sprawdzić odpowiedź na zadanie praktyczne nr 2.
Kliknij tutaj, aby zobaczyć rozwiązanie zadania praktycznego nr 2.
Zadanie praktyczne 3:
Użyj stałej szybkości dla reakcji pomiędzy fenoloftaleiną a jonem OH- do obliczenia początkowej chwilowej szybkości reakcji dla danych doświadczalnych podanych w poprzedniej tabeli.
Kliknij tutaj, aby sprawdzić odpowiedź na zadanie ćwiczeniowe nr 3.
Kliknij tutaj, aby zobaczyć rozwiązanie zadania ćwiczeniowego nr 3.
Różne sposoby wyrażania szybkości reakcji
Zazwyczaj istnieje więcej niż jeden sposób mierzenia szybkości reakcji. Możemy badać rozkład jodku wodoru, na przykład, mierząc szybkość, z jaką powstaje H2 lub I2 w następującej reakcji lub szybkość, z jaką HI jest zużywany.
2 HI(g) H2(g) + I2(g)
Doświadczalnie stwierdzamy, że szybkość, z jaką powstaje I2 jest proporcjonalna do kwadratu stężenia HI w dowolnym momencie czasu.
Co by się stało, gdybyśmy zbadali szybkość powstawania H2? Równanie równowagi sugeruje, że H2 i I2 muszą powstawać dokładnie w tym samym tempie.
Co by się jednak stało, gdybyśmy zbadali szybkość zużywania HI w tej reakcji? Ponieważ HI jest zużywany, zmiana jego stężenia musi być liczbą ujemną. Zgodnie z konwencją, szybkość reakcji jest zawsze podawana jako liczba dodatnia. Dlatego musimy zmienić znak przed podaniem szybkości reakcji dla czynnika, który jest zużywany w reakcji.
Znak ujemny robi dwie rzeczy. Matematycznie, przekształca on ujemną zmianę stężenia HI w dodatnią szybkość. Fizycznie przypomina nam, że stężenie reagenta maleje z czasem.
Jaki jest związek między szybkością reakcji uzyskaną przez obserwację powstawania H2 lub I2 a szybkością uzyskaną przez obserwację zaniku HI? Stechiometria reakcji mówi, że na każdą wytworzoną cząsteczkę H2 lub I2 zużywane są dwie cząsteczki HI. Oznacza to, że szybkość rozkładu HI jest dwukrotnie większa od szybkości powstawania H2 i I2. Zależność tę możemy przekształcić w równanie matematyczne w następujący sposób.
W rezultacie stała szybkości otrzymana z badania szybkości tworzenia się H2 i I2 w tej reakcji (k) nie jest taka sama jak stała szybkości otrzymana z monitorowania szybkości zużywania HI (k’)
Zadanie praktyczne nr 4:
Oblicz szybkość zanikania HI w następującej reakcji w chwili, gdy I2 jest tworzony z szybkością 1.8 x 10-6 moli na litr na sekundę:
2 HI(g) 
H2(g) + I2(g)
Kliknij tutaj, aby sprawdzić swoją odpowiedź do Zadania Ćwiczeniowego 4.
Kliknij tutaj, aby zobaczyć rozwiązanie Zadania Ćwiczeniowego 4.
The Rate Law Versus the Stoichiometry of aReaction
W latach trzydziestych XX wieku Sir Christopher Ingold i współpracownicy z University ofLondon badali kinetykę reakcji substytucji, takich jak poniższe.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Stwierdzili, że szybkość tej reakcji jest proporcjonalna do stężeń obu reagentów.
Rate = k(CH3Br)(OH-)
Gdy przeprowadzili podobną reakcję na nieco innym materiale wyjściowym, otrzymali podobne produkty.
(CH3)3CBr(aq) + OH-(aq) (CH3)3COH(aq) + Br-(aq)
Ale teraz szybkość reakcji była proporcjonalna do stężenia tylko jednego z reagentów.
Rate = k((CH3)3CBr)
Wyniki te ilustrują ważny punkt: Prawo szybkości dla danej reakcji nie może być przewidziane na podstawie stechiometrii reakcji; musi być określone doświadczalnie. Czasami, prawo szybkości jest zgodne z tym, czego oczekujemy od stechiometrii reakcji.
2 HI(g) Rate = k(HI)2
Często, jednak tak nie jest.
| 2 N2O5(g) 4 NO2(g) + O2(g) |
Rate = k(N2O5) |
Rozkład cząsteczek
Niektóre reakcje zachodzą w jednym etapie. Reakcja, w której atom chloru jest przenoszony z ClNO2 na NO, tworząc NO2 i ClNO jest dobrym przykładem reakcji jednoetapowej.
ClNO2(g) + NO(g)
Inne reakcje zachodzą w serii pojedynczych etapów. N2O5, na przykład, rozkłada się do NO2 i O2 w mechanizmie trzystopniowym.
Krok 1: N2O5 Krok 2: NO2 + NO3 Krok 3: NO + NO3 Kroki w reakcji są klasyfikowane pod względem molekularności,która opisuje liczbę zużywanych cząsteczek. Gdy zużywana jest jedna cząsteczka, etap ten nazywany jest jednocząsteczkowym. Kiedy dwie molekuły są konsumowane, jest to dwucząsteczkowe.
Zadanie praktyczne nr 5:
Określ molekularność każdego etapu reakcji, w której N2O5 rozkłada się na NO2 i O2.
Kliknij tutaj, aby sprawdzić odpowiedź na zadanie praktyczne nr 5.
Kliknij tutaj, aby zobaczyć rozwiązanie zadania praktycznego nr 5.
Reakcje mogą być również klasyfikowane pod względem ich kolejności. Rozkład N2O5 jest reakcją pierwszego rzędu, ponieważ szybkość reakcji zależy od stężenia N2O5 podniesionego do pierwszej potęgi.
Rate = k(N2O5)
Rozkład HI jest reakcją drugiego rzędu, ponieważ szybkość reakcji zależy od stężenia HI podniesionego do drugiej potęgi.
Rate = k(HI)2
Gdy szybkość reakcji zależy od więcej niż jednego reagenta, klasyfikujemy reakcję pod względem kolejności każdego z reagentów.
Zadanie praktyczne 6:
Klasyfikuj kolejność reakcji pomiędzy NO i O2 w celu utworzenia NO2:
2 NO(g) + O2(g)
Załóż następujące prawo szybkości dla tej reakcji:
Szybkość = k(NO)2(O2)
Kliknij tutaj aby sprawdzić odpowiedź na zadanie praktyczne 6.
Różnica pomiędzy molekularnością a kolejnością reakcji jest istotna. Cząsteczkowość reakcji lub jej etap opisuje, co dzieje się na poziomie molekularnym. Kolejność reakcji opisuje to, co dzieje się w skali makroskopowej. Określamy kolejność reakcji obserwując pojawianie się produktów reakcji lub znikanie reaktantów. The molecularity of the reactionis something we deduce to explain these experimental results.
Collision Theory Model of Chemical Reactions
The collision theory model of chemical reactions can be used toexplain the observed rate laws for both one-step and multi-step reactions. Model ten zakłada, że szybkość każdego etapu reakcji zależy od częstotliwości zderzeń pomiędzy cząsteczkami zaangażowanymi w ten etap.
Poniższy rysunek stanowi podstawę do zrozumienia implikacji modelu teorii zderzeń dla prostych, jednoetapowych reakcji, takich jak poniższe.
ClNO2(g) + NO(g)
Kinetyczna teoria molekularna zakłada, że liczba zderzeń na sekundę w gazie zależy od liczby cząsteczek na litr. Szybkość tworzenia się NO2i ClNO w tej reakcji powinna być zatem wprost proporcjonalna do stężeń zarówno ClNO2 jak i NO.
Rate = k(ClNO2)(NO)
Model teorii zderzeń sugeruje, że szybkość dowolnego etapu reakcji jest proporcjonalna do stężeń reagentów zużytych w tym etapie. Prawo szybkości dla reakcji jednoetapowej powinno zatem zgadzać się ze stechiometrią tej reakcji.
Na przykład, następująca reakcja zachodzi w jednym etapie.
CH3Br(aq) + OH-(aq)
Gdy te cząsteczki zderzają się w odpowiedniej orientacji, para elektronów niewiązanych na jonie OH- może zostać przekazana atomowi węgla w centrum cząsteczki CH3Br, jak pokazano na poniższym rysunku.
Gdy tak się dzieje, tworzy się wiązanie węgiel-tlen w tym samym czasie, gdy wiązanie węgiel-brom jest zerwane. Wynikiem netto tej reakcji jest zastąpienie jonu OH- jonem Br -. Ponieważ reakcja zachodzi w jednym etapie, który obejmuje zderzenia pomiędzy dwoma reagentami, szybkość tej reakcji jest proporcjonalna do stężenia obu reagentów.
Rate = k(CH3Br)(OH-)
Nie wszystkie reakcje zachodzą w jednym etapie. Poniższa reakcja przebiega w trzech etapach, jak pokazano na rysunku poniżej.
(CH3)3CBr(aq) + OH-(aq)
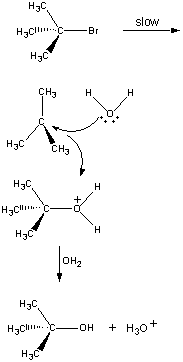
W pierwszym etapie cząsteczka (CH3)3CBr dysocjuje na parę jonów.
Pierwszy krok Dodatnio naładowany jon (CH3)3C+ następnie reaguje z wodą w drugim kroku.
Drugi etap Produkt tej reakcji traci następnie proton na rzecz jonu OH- lub wody w ostatnim etapie.
Trzeci etap Drugi i trzeci etap tej reakcji przebiegają znacznie szybciej niż pierwszy.
(CH3)3CBr Powolny krok (CH3)3C+ + H2O Szybki krok (CH3)3COH2+ + OH- Szybki etap Ogólna szybkość reakcji jest więc mniej więcej równa szybkości pierwszego etapu. Pierwszy etap nazywany jest zatem etapem ograniczającym szybkość reakcji, ponieważ dosłownie ogranicza on szybkość, z jaką mogą powstawać produkty reakcji. Ponieważ tylko jeden odczynnik bierze udział w etapie ograniczającym szybkość reakcji, ogólna szybkość reakcji jest proporcjonalna do stężenia tylko tego odczynnika.
Stężenie = k((CH3)3CBr)
Prawo szybkości dla tej reakcji różni się zatem od tego, co można by przewidzieć na podstawie stechiometrii reakcji. Chociaż w reakcji zużywane są zarówno (CH3)3CBr jak i OH-, szybkość reakcji jest proporcjonalna tylko do stężenia (CH3)3CBr.
Prawa szybkości reakcji chemicznych można wyjaśnić za pomocą następujących ogólnych zasad.
Szybkość dowolnego etapu reakcji jest wprost proporcjonalna do stężeń reagentów zużywanych w tym etapie.
Ogólne prawo szybkości reakcji jest określone przez sekwencję kroków, lub mechanizm, za pomocą którego reagenty są przekształcane w produkty reakcji.
Ogólne prawo szybkości reakcji jest zdominowane przez prawo szybkości dla najwolniejszego kroku w reakcji.
.
