How Many Sides Does A Circle Have?

To pytanie z pracy domowej ze szkoły podstawowej, które powoduje spory wśród doświadczonych matematyków. Aby znaleźć poprawną odpowiedź, wezwałem najbardziej rygorystyczne z instrumentów naukowych, ankietę na Twitterze:

Z perspektywy czasu żałuję, że nie uwzględniłem opcji „żadne z powyższych”, ale więcej na ten temat później. W tym poście zamierzam przejść przez te trzy odpowiedzi (i „Żadna z powyższych”), i omówić ich zalety i wady, jak je widzę, przed dramatycznym ujawnieniem prawidłowej odpowiedzi.

Ale najpierw: dlaczego nie możemy wprost dać prawidłowej odpowiedzi? Słowa w pytaniu są mało tajemnicze. Wszyscy wiemy, co to jest „okrąg”, co to znaczy liczyć „ile” czegoś i co to jest „bok”… a może nie? Oto (przybliżone) definicje, które wydestylowałem z dyskusji z dwoma uczniami szkoły podstawowej, którzy byli na końcu tego pytania:

1. Linia tworząca część granicy kształtu figury płaskiej.

Celem powiedzenia figura płaska zamiast „kształt” tutaj jest to, że chcemy kształty, które żyją w 2 wymiarach (np. kwadraty lub koła, ale nie kule lub sześciany). Kolejnym pytaniem jest to, czym jest „linia” w definicji 1. Oto wariant, który to określa:

2. linia prosta tworząca część granicy figury płaskiej.

Jeśli wpiszesz „define: side” w Google, najbardziej odpowiednią definicją jest:

Figura prostoliniowa to taka, która jest zbudowana z linii prostych. Tak więc ta definicja jest dalszym udoskonaleniem definicji 2, i pozwala nam potwierdzić, że kwadrat ma cztery boki, ale na pierwszy rzut oka nie ma nic do powiedzenia o nieprostoliniowych figurach płaskich, takich jak koła.

Nieskończenie wiele boków?

Myślę, że można bezpiecznie założyć, że respondenci mojej ankiety na Twitterze mają wyższy poziom edukacji matematycznej niż średnia krajowa. Fakt, że byli oni podzieleni na to pytanie w ogóle, i że niewielka większość wybrała odpowiedź, która jest całkiem dobrze niedostępna dla zwykłej publiczności tego pytania (uczniowie szkół podstawowych), z pewnością sugeruje, że coś idzie nie tak gdzieś.

Więc, czy koło ma nieskończenie wiele boków? Zdecydowanie warto rozważyć okrąg jako granicę wielokątów o n bokach, gdy n staje się coraz większe. To jest dokładnie to podejście, które Archimedes, Liu Hui, i niezliczeni inni używali przez wieki do badania geometrii okręgu, włączając w to wymyślanie przybliżeń dla π.

Szesnastowieczne wydanie Jiuzhang suanshu (Dziewięć rozdziałów o sztuce matematycznej) z dynastii Ming, trzeci wiek naszej ery.

Czasami jest absolutnie rozsądne, jako wygodny skrót, myśleć o okręgu jako o wielokącie o nieskończenie wielu bokach.

Ale, jako nieznośny pedant matematyk, chciałbym odróżnić wygodny skrót od dosłownej prawdy. Jeśli jesteśmy pewni, że okrąg jest wielokątem o nieskończenie wielu bokach, to nasuwa się pytanie: jakie są te boki? I z pewnością jedyna wiarygodna odpowiedź brzmi: poszczególne punkty okręgu. Jak długie są te tak zwane boki? Zero centymetrów. A czy te boki są oddzielone rogami? Najwyraźniej nie, albo w ogóle nie ma rogów, albo każdy punkt jest zarówno bokiem, jak i rogiem.

Powiedziałbym, że boki o długości zero są… problematycznym pojęciem. Jak możesz stwierdzić, czy masz jakieś? Na przykład załóżmy, że badam układ, w którym kwadrat powstaje jako granica ośmiokątów w ten sposób:

W tej sytuacji może mieć sens myślenie o moim kwadracie jako mającym osiem boków, z których cztery mają długość zero. Ale gdybym upierał się, że mój (zupełnie zwyczajny) kwadrat naprawdę ma osiem boków, mógłbyś podnieść brew.

Więc ta – zwycięska odpowiedź w mojej ankiecie – jest jedyną, którą zamierzam uznać za definitywnie błędną, a zarazem jedyną, która oferuje jakikolwiek geometryczny wgląd w ogóle. Paradoks? Nie do końca. Rozumowanie przez analogię jest cenną umiejętnością w matematyce i w życiu; jednocześnie ważne jest, aby trzymać się świadomości, że to właśnie robimy.

Dla nieskończenie wielu stron: geometrycznie pouczające.
Przeciw nieskończenie wielu bokom: kwadraty o ośmiu bokach.

Off on a tangent 1: apeirogony

Nawet jeśli koło nie jest jednym z nich, czy istnieją takie rzeczy jak wielokąty o nieskończenie wielu bokach? Cóż, jest słowo, które opisuje takie rzeczy – apeirogon. Regularny apeirogon miałby wtedy boki o równej (niezerowej) długości i równe kąty między nimi. Jedyną opcją jest ten głupio nieciekawy obiekt:

Jeśli masz zastrzeżenia do tego jako do „wielokąta” (albo z powodu kątów 180° albo łańcucha krawędzi nie zamykających się w pętli), co powiesz na coś takiego: zacznij od dołu okręgu, i na każdym etapie poruszaj się wokół połowy tego, co pozostało z okręgu, i zastąp łuk, który właśnie przebyłeś, krawędzią prostą:

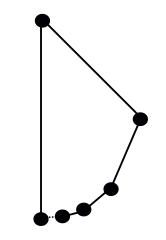
Czy to jest prawdziwy wielokąt? Po raz kolejny zależy to od Twoich pojęć. Zgodnie z jedną z popularnych definicji, „zamkniętego łańcucha wielokątów”, ten nie kwalifikuje się, ponieważ narożnik początkowy (lewy dolny) łączy się tylko z jedną krawędzią. Ale to jest bardzo blisko chybienia: ten punkt jest granicą sekwencji krawędzi od prawej, czyniąc ten kształt „nie-samo-przecinającą się liniową krzywą zamkniętą”, inna definicja wielokąta, której ludzie używają.

Jeśli opuścimy nasz zwykły euklidesowy świat i wejdziemy w przestrzeń hiperboliczną, wtedy nie ma dwuznaczności. Apeirogony (nawet apeirogony regularne) po prostu istnieją:

Kafelkowanie płaszczyzny hiperbolicznej przez apeirogony regularne. (Autor: Anton Sherwood – Praca własna, Domena publiczna, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extreme points

Bardziej uzasadnione może być stwierdzenie, że okrąg ma nieskończenie wiele rogów niż nieskończenie wiele boków (choć nie jest to pytanie, które wydaje się być zadawane bardzo często). Na początek, jeśli narożnik kwadratu jest punktem, w którym jego linia graniczna nie jest prosta, to każdy punkt na okręgu to spełnia. Bardziej zaawansowane jest pojęcie punktu ekstremalnego kształtu: jest to dowolny punkt, przez który można narysować odcinek linii prostej, który dotyka kształtu tylko w tym dokładnym punkcie. Dla kwadratu i wielu znanych kształtów punkty ekstremalne dokładnie pokrywają się z narożnikami. Każdy punkt na granicy okręgu jest punktem ekstremalnym, więc z pewnością jest prawdą, że okrąg ma ich nieskończenie wiele.

Możemy się martwić, że niektóre kształty, takie jak ten szewron, mają rogi, które nie są punktami ekstremalnymi:

Tutaj dolny środkowy róg nie jest punktem ekstremalnym (pozostałe trzy rogi są). Co jest nie tak, to fakt, że ten kształt nie jest wypukły (w przybliżeniu, ma niektóre kawałki wystające zbyt daleko). Okrąg jest wypukły, więc może nie musimy się martwić. Alternatywnie, możemy zaradzić sytuacji definiując „narożnik” jako punkt, który jest skrajnym punktem albo danego kształtu, albo jego dopełnienia, tj. całej płaszczyzny z wyciętym z niej kształtem. Takie podejście pozwoliłoby wykryć narożniki wszystkich wielokątów, w tym szewronu. Dla gładkich krzywych, zidentyfikowałoby wszystkie punkty graniczne jako „rogi”, z wyjątkiem punktów przegięcia (co nie jest nierozsądne, ponieważ możemy argumentować, że granica jest tam prosta).

Jedna strona?

W szkole podstawowej, wydaje się, że „jeden” jest odpowiedzią, która dostaje tick. I jest na to umiarkowanie przyzwoite uzasadnienie. Przypomnij sobie definicję 1 powyżej:

1. Linia stanowiąca część granicy figury płaskiej.

Pierwszym pytaniem jest, co liczy się jako „linia”, szczególnie jeśli nie upieramy się przy prostoliniowości. Jeśli jesteśmy zbyt zrelaksowani w tej kwestii, to można powiedzieć, że każda figura płaska ma „jeden bok”, w tym samym sensie, w jakim ma jedną granicę, obwód lub obwódkę. Ale to musi być błędne, ponieważ na pewno chcemy, żeby kwadrat miał cztery. Cóż, kwadrat ma cztery punkty, w których nie jest gładki, z czterema gładkimi odcinkami pomiędzy nimi. Być może to właśnie te gładkie odcinki liczyliśmy przez cały czas. Mamy więc nowe udoskonalenie definicji 1 (i korzystamy z okazji, by pozbyć się niejasnego terminu „figura”):

4. Każdy gładki odcinek krzywej zamkniętej, gładkiej jak kawałek drogi.

Krzywa zamknięta to taka, która zapętla się, by spotkać się z samą sobą, tak że nie ma wolnych końców. „Piecewise-smooth” oznacza, że jest ona zbudowana z gładkich odcinków, które spotykają się w izolowanych punktach unsmooth. Jest całkowicie uzasadnione, aby chcieć policzyć gładkie odcinki granicy takiego kształtu, i nie jest w żaden sposób oburzające, aby użyć słowa „bok”, gdy to robisz. Więc z pewnością nie twierdzę, że jest to definitywnie zła odpowiedź.

Pytanie brzmi, czy ta interpretacja „boku” jest nie tylko spójna, ale na tyle naturalna, że można ją po prostu założyć bez podawania jej wprost (co rzadko, jeśli w ogóle, ma miejsce). Co się dzieje, gdy gładkość i prostoliniowość liczą się inaczej? Rozważmy ten kształt nagrobka, utworzony przez zastąpienie wierzchołka kwadratu półkolem o równej średnicy.

To ma dwie gładkie części (linię dolną i resztę), ale trzy proste krawędzie (plus zakrzywiony kawałek gładko łączący dwie z nich). Więc ile ma boków? I consulted my Twitter friends again:

This time I should have included „infinitely many” as an option, although that can be absorbed into „None of the above”. Każdy, kto głosował, że koło ma nieskończenie wiele boków, powinien automatycznie zagłosować tutaj na „Żadne z powyższych”, chyba że – ważne zastrzeżenie – natura tego kształtu wskazuje czytelnikowi na inne pojęcie „boku”. Fakt, że najbardziej popularne wybory w tych dwóch ankietach są niezgodne sugeruje, że tak może być (lub przynajmniej wzmacnia, że wody są mętne).

Ale chociaż dwa jest całkowicie godną szacunku odpowiedzią, zgodną z definicją 4 powyżej i z jednostronnością koła, nie jestem zadowolony, że jest to definitywnie właściwa odpowiedź, lub że trzy lub cztery są kategorycznie złe. To zależy, co chcesz liczyć: gładkie odcinki, proste krawędzie, czy proste krawędzie plus to, co potem zostanie, każda z tych odpowiedzi może być odpowiedzią, którą chcesz, w zależności od kontekstu (więcej na ten temat poniżej). W związku z tym nie jestem pewien, czy liczenie liczby gładkich odcinków w pełni odpowiada mojej intuicji dotyczącej słowa „bok”. W końcu dwie pionowe sekcje nagrobka są – myślę, że można to uczciwie powiedzieć – „po przeciwnych stronach”. Czy naprawdę jesteśmy zadowoleni, że są one jednocześnie częścią „tej samej strony”?

Możesz zaprotestować, że mylę dwa różne znaczenia słowa „strona”, że terminologia czasem się ściera i musimy z tym żyć. Ja jednak nie jestem tego taki pewien. Celem tego ćwiczenia jest ekstrapolacja na podstawie sytuacji (figury prostoliniowe), w której te dwa pojęcia całkiem dobrze się zazębiają. Jeśli istniałby nowy pomysł, który uchwyciłby wszystko, co podobało nam się w oryginale, ale jednocześnie stosowałby się do szerszej kategorii kształtów, wtedy miałby on przytłaczające roszczenie do bycia jedyną słuszną odpowiedzią. Ale jeśli wszystkie nasze próby uogólnienia wiążą się z poświęceniem pożądanych aspektów oryginału, to być może nie ma jednego właściwego uogólnienia. Istnieją różne wybory, z różnymi kompromisami, które mogą być odpowiednie w różnych kontekstach (a jeśli jesteśmy w sytuacji, w której więcej niż jeden są w grze, to mogą one być pomocniczo nadawane różne nazwy).

Jest jeszcze jedna wariacja: nagrobek Weierstrassa stworzony przez zastąpienie górnej krawędzi kwadratu przez odcinek funkcji Weiestressa, nieskończenie wiggly linia, która nie jest gładka w dowolnym miejscu.

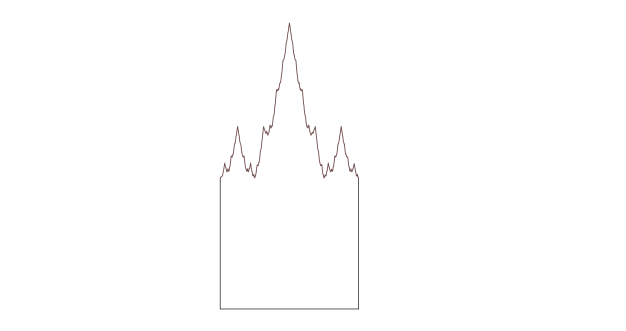
Tutaj (i zauważ literówkę) jest to, co moi przyjaciele z Twittera zrobili z tego – chociaż mniejsza liczba zaryzykowała opinię:

Nie zważając na sceptycyzm moich zwolenników z Twittera, wyjaśnię za chwilę, dlaczego nie uważam, że to głupie widzieć to jako mające cztery boki (z których jeden nie jest gładki). Z drugiej strony, jeśli wolisz, żeby twoje boki były gładkie, to znowu masz wybór między postrzeganiem tego jako mającego nieskończenie wiele boków (z których trzy mają długość 1, a reszta ma długość 0), lub mającego 3 boki plus odcinek granicy zdecydowanie-nie-bocznej.

Dla jednego boku: pojedyncza gładka krzywa.
Przeciwko jednemu bokowi: ten sam bok po przeciwnych stronach.

Off on a tangent 3: sides versus edges

Ile boków ma kwadrat? Cztery. Ile ma krawędzi? Cztery. Więc czy krawędzie i boki to to samo? Niekoniecznie. Oto dwie konfiguracje, które są – przynajmniej przypuszczalnie – każda czteroboczna, ale mają odpowiednio 5 i 3 krawędzie:

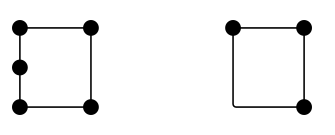
Zwykle, powiedziałbym, „krawędź” jest obiektem topologicznym, w tym, że jego funkcja, a nie kształt, jest tym, co się liczy. Pomyśl o mapie londyńskiego metra. Jeśli zapytałbyś, ile krawędzi jest w tej sieci, nie ma żadnej wartości w sumowaniu prostych lub gładkich odcinków. Liczą się połączenia między stacjami (lub wierzchołkami).

Jak już wspomniano, często myśli się o wielokącie jako o bardzo prostym rodzaju sieci zwanej zamkniętym łańcuchem wielokątów: ciąg wierzchołków (w tym przypadku narożników wielokąta), połączonych krawędziami, w taki sposób, że każdy wierzchołek leży na dokładnie dwóch krawędziach, a całość tworzy pojedynczą pętlę. W tej sytuacji krawędzie i boki są zbieżne, podobnie jak wierzchołki i rogi. Ale na ogół można złamać tę zbieżność, jak w dwóch małych sieciach powyżej.

Jeśli chcesz myśleć o rzeczach sieciowo-teoretycznie, ale wierzchołki nie są wyraźnie zaznaczone, to musisz zgadywać, gdzie one są. W przypadku wielokąta jest to łatwe – wierzchołki są w rogach – i dlatego przełączanie między podejściem geometrycznym i topologicznym przychodzi tak naturalnie. Ale w przypadku innych kształtów, takich jak któryś z powyższych nagrobków, może to nie być takie oczywiste. Niemniej jednak, w każdym z tych przypadków, gdyby powiedziano nam, że gdzieś tam są wierzchołki i poproszono o ich zlokalizowanie, myślę, że rozsądnie byłoby zgadnąć, że są cztery, czyli narożniki oryginalnego kwadratu, a górna krawędź z jakiegoś powodu została przedstawiona jako linia nieprostoliniowa. A jeśli rzeczywiście chcemy myśleć o rzeczach w ten sposób, że każdy z nagrobków ma cztery krawędzie, to może się to wydawać przewrotne (choć logicznie spójne!), aby upierać się, że mają one jakąś inną liczbę boków (zwłaszcza, że wierzchołek jest – pomimo swojej własnej geometrii – wyraźnie „po jednej stronie” figury). W rzeczywistości, zamiast zgadywać, jeden z moich korespondentów na Twitterze zapytał mnie „Czy oba górne wierzchołki zostały usunięte?”, pytanie, które ma sens tylko z perspektywy sieciowo-teoretycznej.

Gdzie to pozostawia koło? Problem polega na tym, że żaden punkt na okręgu nie ma lepszych roszczeń do bycia wierzchołkiem niż jakikolwiek inny. Więc chociaż kuszące (i znów spójne) jest postrzeganie okręgu jako sieci z jedną krawędzią, jeśli zamierzamy wstawić wierzchołki, nie ma oczywistego powodu, by preferować jeden z nich zamiast jakiejkolwiek innej liczby.

Czy możemy postrzegać go jako sieć bez wierzchołków, coś w rodzaju linii metra bez stacji? Zwykła matematyczna koncepcja sieci nie pozwoliłaby na to, ale to nie powinno nas zbytnio zniechęcać. To sugeruje podejście czysto topologiczne. Problem polega na tym, że z tego punktu widzenia, podczas gdy koło może być rodzajem sieci bez wierzchołków i z jedną krawędzią, tak samo jest z kwadratem (jeśli tak się składa, że linia metra jest ułożona). W topologii, kwadrat jest kołem. (To nie jest paradoks, to po prostu stwierdzenie, że granica jest pojedynczą pętlą, której kształt nie ma znaczenia). Więc podczas gdy ten rodzaj sieci ma „jedną krawędź”, oczywiście kwadrat nie ma „jednego boku”, więc związek między bokami (geometryczny) i krawędziami (topologiczny) ponownie się załamał, tak jak w dwóch małych sieciach przedstawionych powyżej. Więc to podejście nie prowadzi nas zbyt daleko do przodu.

No Sides?

Może wydawać się paradoksalne twierdzenie, że koło (lub jakikolwiek kształt) nie ma „żadnych boków”. Ale argument na obronę jest prosty. Wracamy do definicji 2:

2. linia prosta stanowiąca część granicy figury płaskiej.

Jest to proste, łatwo zrozumiałe sformułowanie, które doskonale oddaje boki kwadratu. Nie udało nam się znaleźć zadowalającego uogólnienia tego na figury zakrzywione, więc najlepiej pozostać przy oryginale. A koło nie ma żadnych boków.

Dla braku boków: prawda, zgodnie z sensownym pojęciem „bok”.
Przeciwko braku boków: brzmi jak koan zen.

None of the Above?

Przypomnij sobie definicję dostarczoną przez Google:

3. każda z linii tworzących granicę płaskiej figury prostoliniowej.

Próba zastosowania tego do koła – figury nieprostoliniowej – nie daje nic. Pytanie jest tak samo bezsensowne jak „Ile boków ma poniedziałek?”

Ponieważ definicja 3 jest najbardziej oficjalna (jedyna w tym poście nie wymyślona przeze mnie lub moje dzieci), czyż nie czyni to „Żadnego z powyższych” kategorycznie poprawną odpowiedzią? Może. Z drugiej strony: kiedy ktoś zadaje nam pytanie, zasada dobroczynności być może wymaga, byśmy założyli, że jest ono sensowne, chyba że możemy stanowczo stwierdzić inaczej, a definicje 1, 2, 4 i inne warianty to umożliwiają. Co więcej, definicja 3 jest raczej językowa niż formalnie matematyczna, a zatem jest raczej opisowa niż normatywna, więc nie powinniśmy być przez nią skrępowani.

Za żadnym z powyższych: semantyczna usterka.
Przeciw żadnemu z powyższych: dialogiczna dobroczynność.

Właściwa odpowiedź

Co skłoniło mnie do napisania tego postu? Podobnie jak niezliczeni uczniowie szkoły podstawowej, moi pięcioletni bliźniacy – wspomniani na początku uczniowie szkoły podstawowej – otrzymali ostatnio to pytanie jako zadanie domowe. Jeden opowiedział się za „1”, a drugi za „0”, a ja starałem się uchwycić i rozwinąć ich rozumowanie powyżej. Myślę, że obie odpowiedzi są całkowicie do obrony – i żadna nie jest definitywnie right.

Więc, co powinieneś zrobić, jeśli zostaniesz zapytany: Ile boków ma koło? Moim zdaniem, optymalną odpowiedzią jest zwrócenie się do matematyka w twoim życiu, aby napisał na ten temat rozprawę liczącą 3000 słów, którą następnie możesz wydrukować i triumfalnie wręczyć swojemu nieszczęsnemu nauczycielowi. Ale jeśli to się nie uda, najlepszym podejściem jest pójście za przykładem Sokratesa i odpowiedzenie na pytanie kontrpytaniem: What do you mean by „side”?

Gdy wszystko jest powiedziane i zrobione, liczenie do zera, lub do jednego, lub odmowa odpowiedzi na pytanie, nie mówi nam praktycznie nic o geometrii okręgów. Ale można wiele zyskać, rozdzielając znane pojęcia, zrzucając lub dodając dodatkowe warunki, kwestionując naszą intencję poprzez przejście z jednego kontekstu do nieco innego i próbując dokładnie zapisać, co rozumiemy przez dane pojęcie w danym kontekście. Na tym właśnie polega prawdziwa matematyka.

Przypisy

Można zrobić coś innego: np. wybrać punkt początkowy P na okręgu, z którego będziemy mierzyć odległość po obwodzie. Następnie zadeklarować, że punkty w racjonalnej odległości od P są rogami, a pozostałe są bokami. W efekcie otrzymamy nieprzeliczalnie nieskończoną liczbę rogów i nieprzeliczalnie nieskończoną liczbę boków. Można też zastrzec, że jest odwrotnie. To może być wygodne dopasowanie do wielokątnego podejścia granicznego do okręgów, ale trudno mi się zgodzić, że jest to łatwe lub wystarczająco oczywiste, aby uznać to za „właściwą odpowiedź”.

Jeden z moich korespondentów na Twitterze martwił się o to, jak gładka jest krzywa. Ten nagrobek jest stale różniczkowalny, ale nie dwa razy tak. Byłoby z pewnością interesujące, gdyby wiele osób uważało, że jest to sprawa krytyczna, a to prawdopodobnie można przetestować za pomocą nieskończenie gładkiego nagrobka zbudowanego z czegoś takiego, chociaż nie przemyślałem szczegółów.

Możemy spróbować sformalizować to w następujący sposób: w kwadracie (lub dowolnym wielokącie), strona ma własność, że zaczynając od dowolnej pozycji we wnętrzu, możesz przeciąć kształt prosto przez swoją lokalizację, tak że wybrana strona jest mocno po jednej stronie cięcia. To nie działa w przypadku dwustronnego nagrobka: każde cięcie zawsze przetnie dłuższy bok. Możemy to osłabić, mówiąc, że aby liczyć się jako bok, musi istnieć przynajmniej jeden sposób na przecięcie kształtu tak, aby bok znajdował się po jednej stronie cięcia. To pozwoliłoby nam powiedzieć, że nagrobek ma cztery boki (nawet jeśli zakrzywiona część nie jest po jednej stronie punktów w górnym regionie). Dla okręgu jednak, jego domniemany jeden bok nigdy nie jest na jednym boku (więc byłby wykluczony), i tylko prosty odcinek półkola liczyłby się jako bok.

Nie jest łatwo wymyślić rygorystyczne uzasadnienie, które działa dla obu nagrobków, ale myślę bardziej nieformalnie w kategoriach punktów Schellinga: to znaczy lokalizacji, które wyróżniają się jako specjalne z powodów, które mogą nie być łatwe do przewidzenia z góry.

Podziękowania

Dziękuję wszystkim, którzy uczestniczyli lub retweetowali moje ankiety, lub dyskutowali ze mną na Twitterze.