Wymagania wstępne – Podstawy teorii grafów – zestaw 1
Graf jest strukturą stanowiącą zbiór obiektów, w którym pewne pary obiektów są w pewnym sensie „powiązane”. Obiektom grafu odpowiadają wierzchołki, a relacjom między nimi – krawędzie. Graf jest przedstawiany schematycznie jako zbiór kropek przedstawiających wierzchołki połączonych liniami lub krzywymi przedstawiającymi krawędzie.
Formalnie,
„Graf 
składa się z 
, niepustego zbioru wierzchołków (lub węzłów) i 
, zbioru krawędzi. Każda krawędź ma albo jeden albo dwa wierzchołki z nią związane, zwane jej punktami końcowymi.”
Typy grafów :Istnieje kilka typów grafów rozróżnianych na podstawie krawędzi, ich kierunku, wagi itp.
1. Graf prosty – Graf, w którym każda krawędź łączy dwa różne wierzchołki i w którym żadne dwie krawędzie nie łączą tej samej pary wierzchołków nazywamy grafem prostym. Na przykład, rozważmy następujący graf –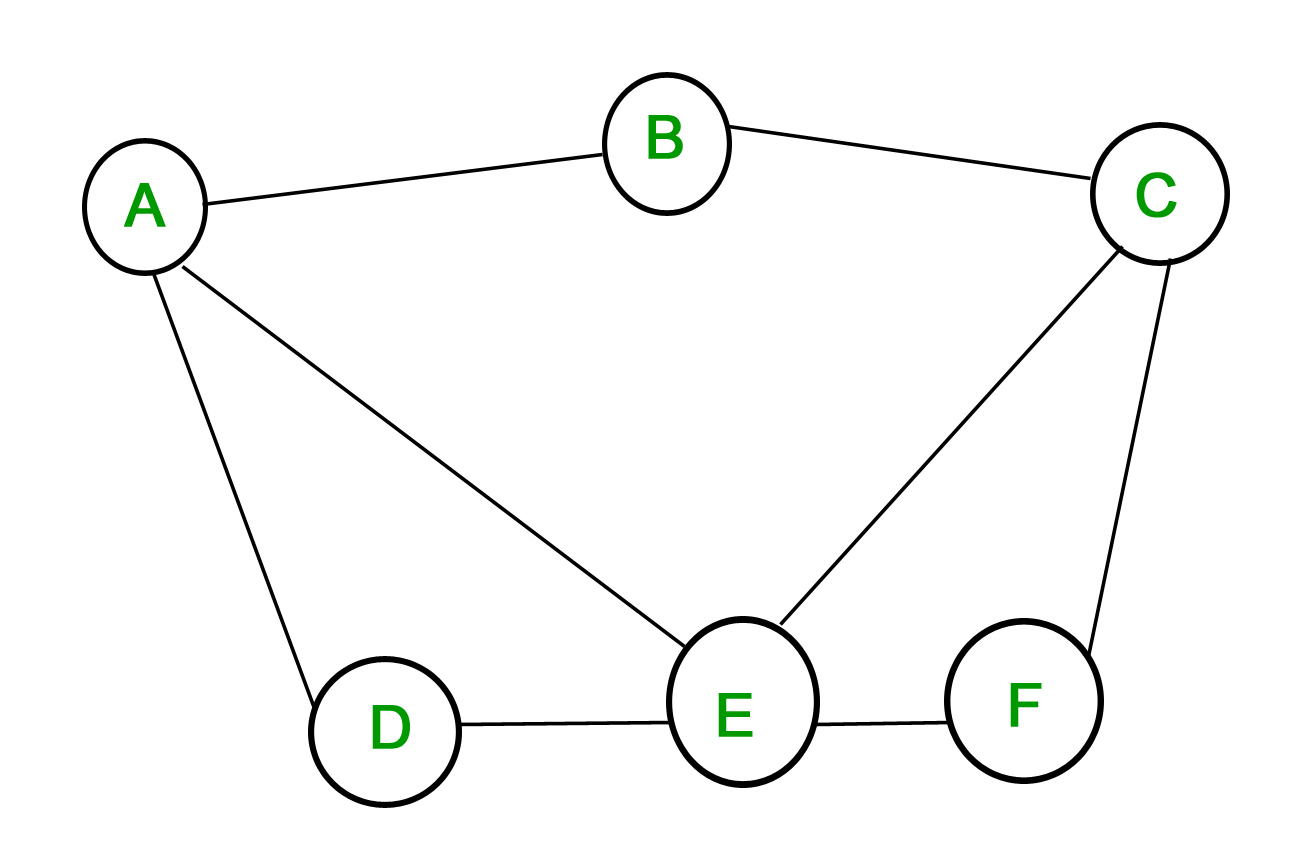
Powyższy graf jest grafem prostym, ponieważ żaden wierzchołek nie ma samopętli i żadne dwa wierzchołki nie mają więcej niż jedną łączącą je krawędź.
Krawędzie są oznaczane przez wierzchołki, które łączą- 
jest krawędzią łączącą wierzchołki 
i 
.
2. Multigraf – Graf, w którym wiele krawędzi może łączyć tę samą parę wierzchołków, nazywamy multigrafem.
Ponieważ między tą samą parą wierzchołków może być wiele krawędzi, krotność krawędzi mówi o liczbie krawędzi między dwoma wierzchołkami.
Powyższy graf jest multigrafem, ponieważ między i 
jest wiele krawędzi. Krotność krawędzi 
wynosi 2.
W niektórych grafach, w przeciwieństwie do przedstawionego powyżej, krawędzie są skierowane. Oznacza to, że relacja między obiektami jest jednokierunkowa, a nie dwukierunkowa. Kierunek krawędzi może być istotny w niektórych zastosowaniach.
Na podstawie tego, czy krawędzie są skierowane czy nie, możemy mieć grafy skierowane i grafy nieskierowane. Tę własność można rozszerzyć na grafy proste i multigrafy, aby otrzymać proste grafy skierowane lub nieskierowane oraz skierowane lub nieskierowane multigrafy.
Podstawowa terminologia grafów :
W powyższej dyskusji niektóre terminy dotyczące grafów zostały już wyjaśnione, takie jak wierzchołki, krawędzie, krawędzie skierowane i nieskierowane itd. Istnieje więcej terminów, które opisują właściwości wierzchołków i krawędzi.
- Adjacency – W grafie
dwa wierzchołki 
i 
mówi się, że są sąsiednie, jeśli są punktami końcowymi krawędzi. Mówi się, że krawędź 
jest incydentna z tymi wierzchołkami.
W przypadku, gdy krawędź jest skierowana, mówi się, że jest przyległa do , a jest przyległa od . Tutaj mówi się, że jest wierzchołkiem początkowym, a jest wierzchołkiem końcowym. - Stopień – Stopień wierzchołka jest liczbą krawędzi z nim sąsiadujących, z wyjątkiem samopętli, która przyczynia się dwukrotnie do stopnia wierzchołka. Stopień wierzchołka jest oznaczany jako
.
W przypadku grafów skierowanych, stopień jest dalej klasyfikowany jako in-degree i out-degree. Stopień wewnętrzny wierzchołka to liczba krawędzi z danym wierzchołkiem jako wierzchołkiem końcowym. Stopień wyjściowy wierzchołka jest liczbą krawędzi z danym wierzchołkiem jako wierzchołkiem początkowym. In-degree jest oznaczany jako
i out-degree jest oznaczany jako 
.
Na przykład w grafie skierowanym pokazanym powyżej przedstawiającym loty między miastami, in-degree wierzchołka „Delhi” wynosi 3 i jego out-degree jest również 3.
Uwaga: Jeśli wierzchołek ma zero stopni, jest nazywany izolowanym. Jeśli jego stopień wynosi jeden to nazywamy go wisielcem.
Twierdzenie uścisku dłoni :
Co byśmy otrzymali, gdyby stopnie wszystkich wierzchołków grafu zostały dodane. W przypadku grafu nieskierowanego, każda krawędź wnosi dwa razy, raz dla swojego początkowego wierzchołka i drugi dla swojego końcowego wierzchołka. Zatem suma stopni jest równa dwukrotności liczby krawędzi. Fakt ten jest stwierdzony w twierdzeniu Handshaking Theorem.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Twierdzenie Handshaking Theorem, dla grafów nieskierowanych, ma ciekawy wynik –
An undirected graph has an even number of vertices of odd degree.
Dowód : Niech 
i 
będą zbiorami wierzchołków o stopniach odpowiednio parzystych i nieparzystych.
Z twierdzenia o podawaniu rąk wiemy, że,
Więc,
Suma stopni wierzchołków o stopniach parzystych jest parzysta. LHS jest również parzysta, co oznacza, że suma stopni wierzchołków o stopniach nieparzystych musi być parzysta.
Więc liczba wierzchołków o stopniach nieparzystych jest parzysta.
Kilka szczególnych grafów prostych :
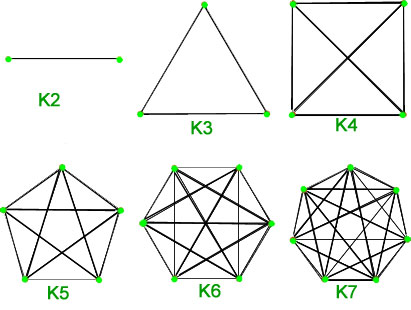
1. Grafy zupełne – Graf prosty o 
wierzchołkach mający dokładnie jedną krawędź między każdą parą wierzchołków nazywamy grafem zupełnym. Graf zupełny o wierzchołkach jest oznaczany przez 
. Całkowita liczba krawędzi wynosi n*(n-1)/2 przy n wierzchołkach w grafie zupełnym.
2. Cykle – Cykle są grafami prostymi o wierzchołkach 
i krawędziach 
. Cykl o wierzchołkach jest oznaczany jako 
. Całkowita liczba krawędzi wynosi n przy n wierzchołkach w grafie cyklu.
3. Koła – Koło jest takie samo jak cykl, z jednym dodatkowym wierzchołkiem, który jest połączony z każdym innym wierzchołkiem. Koła składające się z wierzchołków z 1 dodatkowym wierzchołkiem są oznaczane przez 
. Całkowita liczba krawędzi wynosi 2*(n-1) przy n wierzchołkach w grafie kołowym.
4. Hipersześcian – Hipersześcian lub n-sześcian jest grafem o 
wierzchołkach, z których każdy jest reprezentowany przez n-bitowy ciąg znaków. Wierzchołki różniące się o co najwyżej 1 bit są połączone krawędziami. Hipersześcian o wierzchołkach jest oznaczany przez 
. Całkowita liczba krawędzi wynosi n*
przy wierzchołkach w grafie sześciennym.
5. Grafy dwudzielne – O grafie prostym mówimy, że jest dwudzielny, jeśli jego zbiór wierzchołków można podzielić na dwa rozłączne zbiory takie, że każda krawędź w ma swój wierzchołek początkowy w pierwszym zbiorze, a wierzchołek końcowy w drugim zbiorze. Całkowita liczba krawędzi wynosi (n*m) przy (n+m) wierzchołkach w grafie dwudzielnym.
Twierdzenie – Graf prosty jest dwudzielny wtedy i tylko wtedy, gdy możliwe jest przypisanie każdemu wierzchołkowi grafu jednego z dwóch
różnych kolorów tak, że żadne dwa sąsiednie nie są przypisane do tego samego
koloru.
O grafie dwudzielnym z 
i wierzchołkami w jego dwóch rozłącznych podzbiorach mówi się, że jest kompletny, jeśli istnieje krawędź od każdego wierzchołka w pierwszym zbiorze do każdego wierzchołka w drugim zbiorze, w sumie 
krawędzi. Kompletny graf dwudzielny z wierzchołkami w pierwszym zbiorze i wierzchołkami w drugim zbiorze jest oznaczany jako 
.
GATE CS Corner Questions
Praktykowanie poniższych pytań pomoże Ci sprawdzić swoją wiedzę. Wszystkie pytania zostały zadane w GATE w poprzednich latach lub w GATE Mock Tests. Zaleca się, abyś je przećwiczył.
1. GATE CS 2013, pytanie 25
2. GATE CS 2014 Set-1, pytanie 61
3. GATE CS 2006, pytanie 71
4. GATE CS 2002, pytanie 25
5. GATE CS 2004, pytanie 37
6. GATE CS 2014 Set-2, pytanie 13
References-
Graphs – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen
This article is contributed by Chirag Manwani. Jeśli podoba Ci się GeeksforGeeks i chciałbyś się przyczynić do jego powstania, możesz również napisać artykuł korzystając z adresu contribute.geeksforgeeks.org lub wysłać go pocztą na adres [email protected]. Zobacz, jak twój artykuł pojawia się na stronie głównej GeeksforGeeks i pomóż innym Geekom.