Dyfrakcja rentgenowska jest powszechnie stosowaną techniką charakteryzacji materiałów, która pozwala na identyfikację orientacji krystalicznej i odstępów międzyatomowych. Promienie rentgenowskie są używane do tego, ponieważ długość fali jest na tej samej skali długości, jak odstępy międzyatomowe i wartości parametrów sieci.
Co się dzieje?
Promieniowanie rentgenowskie jest generowane w rurze próżniowej przez ogrzewanie włókna wolframowego powyżej jego funkcji roboczej, aby wyrzucić elektrony. Warunki próżni są niezbędne w celu zwiększenia średniej drogi swobodnej elektronów. Elektrony są przyspieszane do katody miedzianej z energii na rzędu 25 keV. Zderzenia elektronów z miedzianą katodą powodują jonizacje powłoki wewnętrznej, wytwarzając promieniowanie rentgenowskie, ponieważ elektrony o wyższej energii opadają, aby wypełnić puste miejsca o niższej energii. Elektrony z różnych wyższych poziomów energetycznych opadają, wytwarzając fale elektromagnetyczne o różnej energii. W ten sposób generowane jest promieniowanie rentgenowskie o wielu długościach fali (typu K-beta i K-alfa). Dla dyfrakcji rentgenowskiej idealne jest światło monochromatyczne oddziałujące z próbką, dlatego promieniowanie K-beta jest odfiltrowywane za pomocą płytki niklowej. Chociaż rzeczywiście istnieją dwie powiązane energie K-alfa, energie te są tak podobne, że nie wpływa to znacząco na ogólny profil piku. Promieniowanie rentgenowskie przechodzi przez kolimator w celu regulacji szerokości wiązki.
Trochę tła z prawem Bragga
Prawo Bragga opisuje zależność dla interferencji konstruktywnej, gdzie promieniowanie rentgenowskie o długości fali λ padające na materiał pod kątem θ jest rozpraszane przez płaszczyzny krystaliczne oddzielone od siebie odległością d, a n oznacza liczbę całkowitą.
Jak widać poniżej, przesunięcie fazowe w fali powoduje albo konstruktywną inferencję, jak pokazano po lewej stronie, albo destrukcyjną interferencję, przedstawioną po prawej stronie, zgodnie z kątem 2θ.
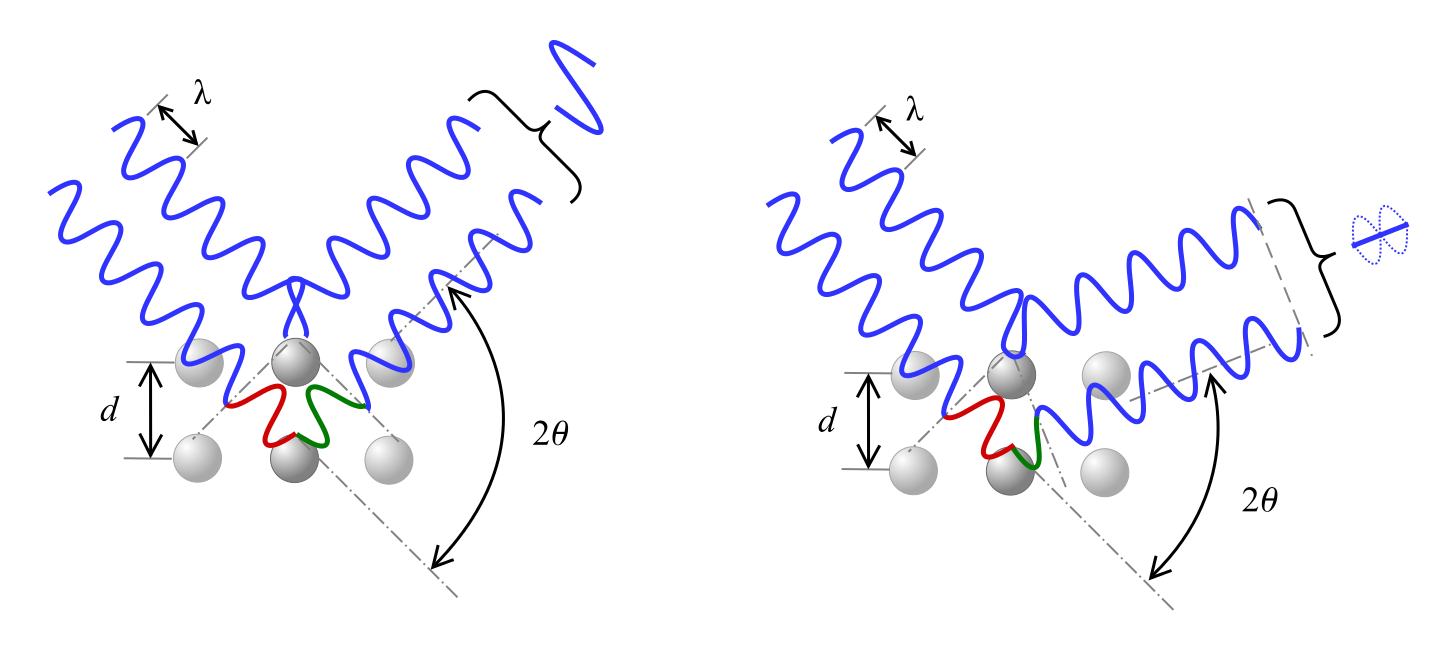
Równania na interpretację wyników XRD
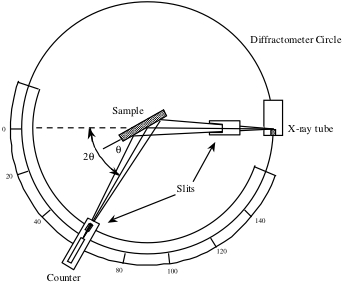
Licznik, widoczny poniżej na schemacie dyfraktometru rentgenowskiego, jest obracany w zakresie wartości 2θ i rejestruje intensywność sygnału rentgenowskiego odbitego od kryształu w każdej pozycji. Ta intensywność mierzona jako funkcja 2θ jest używana do generowania profilu piku.
Dla kątów, które spełniają warunek Bragga, pik w sygnale rentgenowskim będzie obserwowany z powodu konstruktywnej interferencji. Te piki są następnie wykorzystywane do identyfikacji kierunków krystalicznych i obliczania parametrów sieciowych. Dla układów sześciennych, odległość międzypłaszczyznowa, d, może być obliczona przez następujące równanie wyprowadzone z geometrii kryształu, gdzie a jest parametrem sieci, a h, k, i l są indeksami Millera.
Połączenie prawa Bragga i odległości międzypłaszczyznowych daje następujące równanie.
Tutaj przenieśliśmy wszystkie stałe na lewą stronę równania, co pozwala nam porównywać stosunki wartości sin2(θ) i indeksów Millera pomiędzy różnymi pikami.
Gdy padająca fala elektromagnetyczna uderza w materiał próbki, elektrony rezydujące w materiale są zaburzone w oscylujący wzór, który generuje nowe promienie rentgenowskie i efektywnie rozprasza padające fale świetlne. Występują dwa rodzaje rozpraszania: koherentne lub elastyczne rozpraszanie polega na ciasno związanych oscylujących elektronach, które rozpraszają promienie rentgenowskie o tej samej długości fali, oraz rozpraszanie niekoherentne, które występuje, gdy luźno związane elektrony są wprawiane w ruch oscylacyjny i generują promienie rentgenowskie o różnej energii. Dyfrakcja rentgenowska mierzy intensywność spójnie rozproszonego promieniowania rentgenowskiego, które osiąga szczyt w miejscu konstruktywnej interferencji fal. Współczynnik rozpraszania atomowego może być zdefiniowany jako stosunek amplitudy fali rozproszonej przez atom do amplitudy fali rozproszonej przez pojedynczy elektron. Stosunek ten zasadniczo opisuje efektywność rozpraszania atomu dla danego kierunku.
Przykład danych XRD
Tutaj są dane zebrane z eksperymentu, który wykonałem podczas mojego licencjackiego kursu laboratoryjnego próbując zidentyfikować nieznany metal na podstawie jego struktury krystalicznej.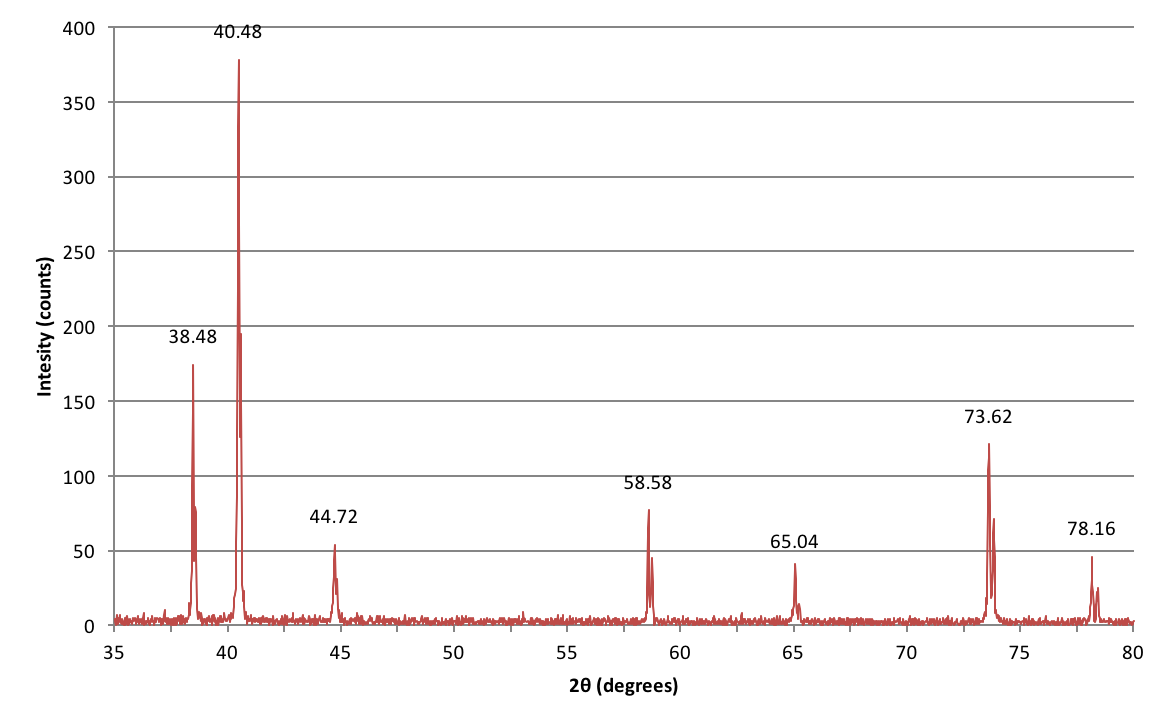
Jak zinterpretować te piki?
| Struktura kryształu | Warunki |
|---|---|
| Simple Cubic | wszystkie wartości h, k, l |
| Body Centered Cubic | h+k+l muszą być parzyste |
| Face Centered Cubic | h, k, and l must be all odd or all even |
Structure factors account for instances where a plane may exist halfway between two neighboring planes and causes destructive interference to occur. Czynniki te skutkują zestawem reguł dla różnych geometrii struktury kryształu, które określają, kiedy może wystąpić konstruktywna interferencja. Powyższa tabela zawiera listę parametrów indeksu Millera, w których wystąpi interferencja konstruktywna. Bardziej rozbudowana tabela jest przedstawiona poniżej. Porównując stosunki sin2θ (oznaczane jako $Q^2$ w drugiej tabeli) dla różnych pików dyfrakcyjnych, można określić strukturę kryształu i indeksy Millera.
.
.
.
X-…Dyfrakcja promieniowania ma szeroki zakres zastosowań do charakteryzacji materiałów. Może być stosowana jako metoda doświadczalna do eksperymentalnego wyznaczania objętości komórki jednostkowej do teoretycznych obliczeń gęstości. Dodatkowo, jeśli materiał jest poddany naprężeniom szczątkowym, zniekształcona siatka będzie wykazywać zakres d-rozstawów, które spełniają prawo Bragga, co skutkuje znacznie szerszymi pikami dyfrakcyjnymi. Szerokość piku dyfrakcyjnego może być również wykorzystywana do określania wielkości cząstek.
.