Kwadratuursignalen, ook wel IQ signalen, IQ data of IQ samples genoemd, worden vaak gebruikt in RF toepassingen. Zij vormen de basis van complexe RF signaalmodulatie en -demodulatie, zowel in hardware als in software, en ook in complexe signaalanalyse. In dit bericht wordt ingegaan op het concept van IQ-signalen en hoe ze worden gebruikt.
Van een paar periodieke signalen wordt gezegd dat ze in “kwadratuur” zijn als ze 90 graden in fase verschillen. Het “in-fase” of referentiesignaal wordt “I” genoemd, en het signaal dat 90 graden is verschoven (het kwadratuursignaal) wordt “Q” genoemd. Wat betekent dit en wat maakt het ons uit? Laten we beginnen met de grondbeginselen.
Basisbeginselen van RF-modulatie
Ik zal beginnen met een overzicht van eenvoudige RF-modulatie. Een ongemoduleerde RF draaggolf is eenvoudigweg een sinusgolf, zoals hieronder afgebeeld.
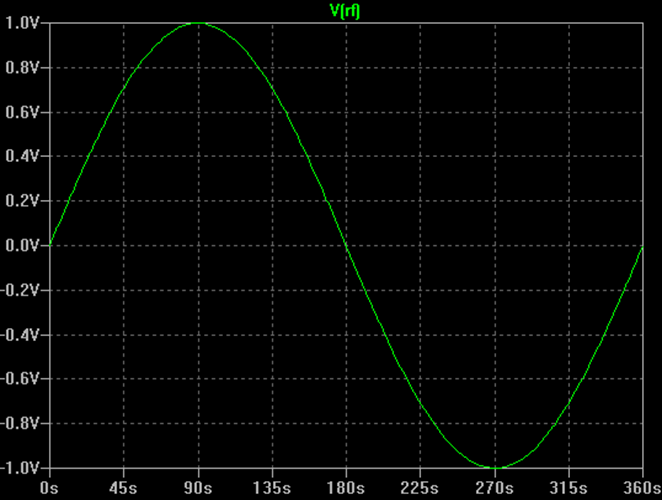
Het signaal kan als functie van de tijd worden beschreven met de volgende vergelijking:
V(t) = A * sin (2 * π * f * t + Ф)
waarin:
A: de piekamplitude is
f: de frequentie is
t: de tijd is
Ф: de faseverschuiving is
Informatie wordt “gedragen” door een RF-draaggolf door middel van het proces van modulatie. Het informatiesignaal (spraak, gegevens, enz.) wordt gebruikt om de eigenschappen van het RF-signaal te veranderen. Een eenvoudig voorbeeld is Amplitudemodulatie, of AM.
Voor AM wordt het informatiesignaal gebruikt om de amplitude van de draaggolf te veranderen, of te moduleren. Wiskundig kan dit worden voorgesteld door de constante “A” in de vorige vergelijking te veranderen in een tijdsvariërend signaal (het informatiesignaal):
V(t) = A(t) * sin (2 * π * f * t + Ф)
Het informatiesignaal, ook bekend als het basisbandsignaal, varieert veel langzamer met de tijd dan het RF-signaal doet. Daarom moet, om het effect van de modulatie te zien, de omhullende van het RF-signaal over een langere tijdschaal worden bekeken, zoals hieronder is aangegeven.
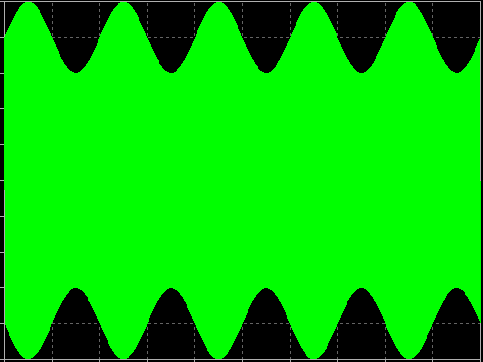
In dit geval is het A(t) signaal een sinusoïde. De figuur laat zien hoe de amplitude van het RF-signaal het sinusoïdale A(t) basisbandsignaal volgt.
U kunt dit uitbreiden door te erkennen dat andere eigenschappen van de RF-draaggolf kunnen worden veranderd, of gemoduleerd, door een basisbandsignaal tegen de tijd. Als de frequentie wordt gemoduleerd door een basisbandsignaal, heb je Frequentie Modulatie (FM). Op dezelfde manier, als de fase wordt gemoduleerd, heb je Fasemodulatie (PM). Dus:
- A(t) is wanneer de amplitude wordt gevarieerd t.o.v. de tijd
- f(t) is wanneer de frequentie wordt gevarieerd t.o.v. de tijd
- Ф(t) is wanneer de fase wordt gevarieerd t.o.v. de tijd.
Houd het basisconcept van modulatie in gedachten als we het concept van kwadratuursignalen erbij betrekken…
Kwadratuursignaalconcepten
Als het faseverschil Ф tussen twee sinusoïden 90 graden is (of π /2 radialen), dan wordt gezegd dat deze twee signalen kwadratuur zijn. Een voorbeeld hiervan is de sinusgolf en de cosinusgolf.
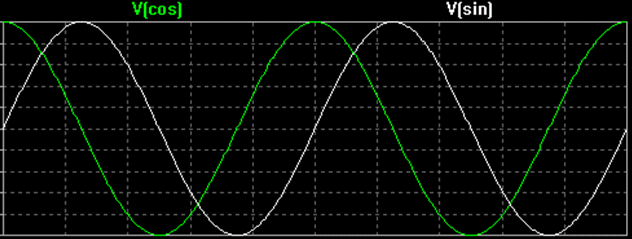
Overeengekomen is de cosinusgolf de in-fase-component en de sinusgolf de kwadratuur-component. De hoofdletter I staat voor de amplitude van het in-fase signaal en de hoofdletter Q voor de amplitude van het kwadratuursignaal.
Vierfasesignalen gebruiken om te moduleren
Er gebeuren interessante dingen wanneer u kwadratuursignalen bij elkaar optelt.
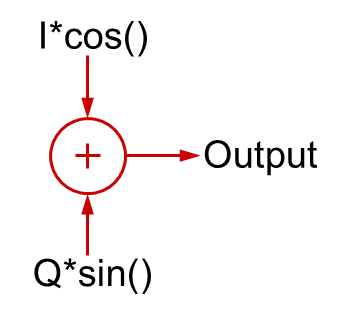
Als I=1 en Q=0, dan zou u eenvoudigweg de cosinusgolf hebben (fase gelijk aan 0). Op dezelfde manier, als I=0 en Q=1, zou u de sinusgolf hebben, dat is het 90 graden verschoven signaal.
Als zowel I als Q gelijk waren aan 1, dan zal de som een nieuw signaal zijn dat hieronder grafisch wordt weergegeven.
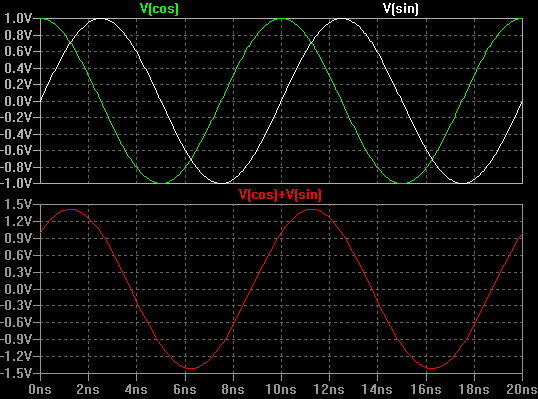
Merk op dat het optellen van deze twee kwadratuursignalen van gelijke amplitude resulteert in een nieuwe sinusoïde die 45 graden in fase is verschoven.
U ziet nu dat de amplitude en de fase van de som van de kwadratuursignalen een functie is van de waarde van I en Q. Daarom kunt u gemoduleerde RF-signalen maken door de I- en Q-waarden te variëren ten opzichte van de tijd. Laten we een paar voorbeelden bekijken.
Digitale RF-modulatievoorbeelden
Als Q=0, en I wordt gewijzigd tussen +1 en -1 in de tijd, dan creëert u een Binary Phase Shift Keyed RF-signaal (BPSK):
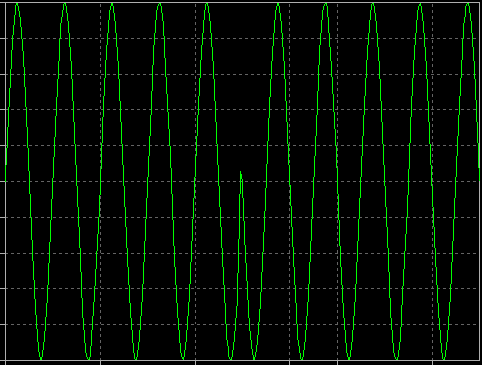
Het I(t)-signaal zou een eenvoudige digitale bitstroom kunnen zijn. Als u dat signaal de versterking van de RF-sinusoïde tussen +1 en -1 laat regelen, hebt u een BPSK-signaal gecreëerd.
Nemen we een stap verder… Als twee digitale bits worden gebruikt om de I en Q waarden tussen +1 en -1 in de tijd te sturen, dan kan de resulterende som van de kwadratuursignalen een van de vier verschillende fasen zijn:
- I=+1 & Q=+1 resulteert in 45 graden fase
- I=-1 & Q=+1 resulteert in 135 graden fase
- I=-1 & Q=-1 resulteert in 225 graden fase
- I=+1 & Q=-1 resulteert in 315 graden fase
Dit staat bekend als Quadrature Phase Shift Keying modulatie (QPSK). Dit zijn twee voorbeelden van kwadratuur-amplitudemodulatie (QAM). De verschillende modulatietoestanden voor QAM worden vaak weergegeven in een constellatiediagram. Een constellatiediagram is eenvoudigweg een fasordiagram dat de amplitude en fase van een signaal weergeeft als een polaire plot.
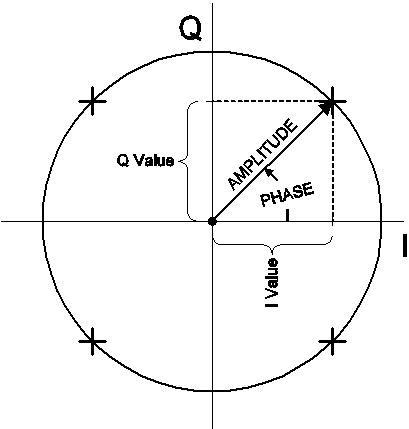
De lengte van de vector vanaf de oorsprong vertegenwoordigt de signaalmagnitude, en de hoek die de vector vormt met de horizontale as vertegenwoordigt de fase. De vier “toestanden” voor het hierboven beschreven QPSK-signaal worden weergegeven als de vier “+”-symbolen in het diagram. U zult ook opmerken dat de horizontale as is gelabeld met “I” en de verticale as met “Q” – omdat deze de I- en Q-componentwaarden voorstellen die bij het signaal horen.
Meer complexe QAM-modulaties, zoals 16QAM, hebben eenvoudigweg meer toestanden. Voor 16QAM kunnen de I- en Q-waarden elk een van de vier discrete waarden hebben, hetgeen resulteert in 16 mogelijke combinaties. Dit resulteert in 16 combinaties van amplitude en fase voor het RF-signaal.
Quadrature Signals Everywhere
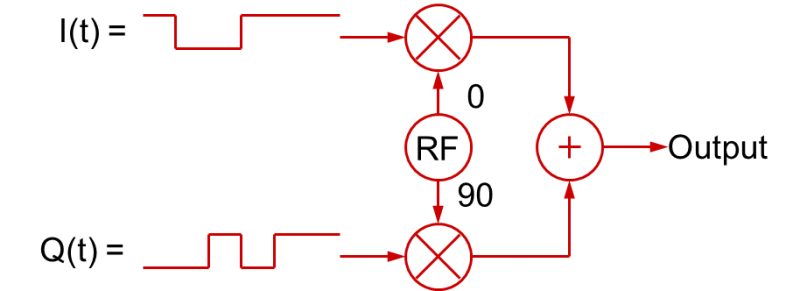
Het gebruik van in de tijd variërende I- en Q-signalen om gemoduleerde RF-signalen te creëren is niet beperkt tot digitale basisbandsignalen. De I(t) en Q(t) basisbandsignalen kunnen ook analoge basisbandsignalen zijn. In feite, in de meeste “digitaal” gemoduleerde RF toepassingen zoals QPSK of nQAM, worden de basisbandsignalen gefilterd om de overgangen te vertragen. Dit wordt gedaan om de bandbreedte van het gemoduleerde RF signaal te beperken (snelle digitale stijg- en daaltijden nemen veel bandbreedte in beslag!). Deze gefilterde digitale signalen zijn in feite analoge signalen! In meer algemene zin kan het kwadratuurmodulatieproces dus worden geïllustreerd zoals in deze figuur:
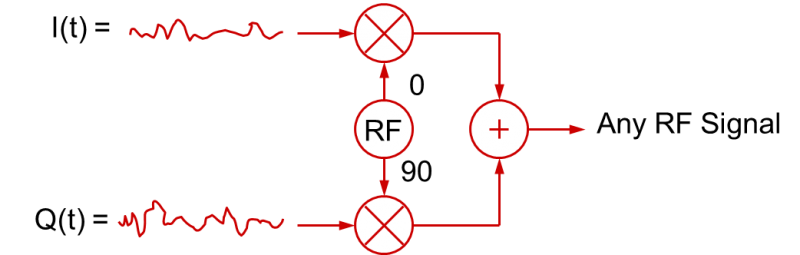
De algemene conclusie die u hieruit kunt trekken is dat een RF-signaal met om het even welk type modulatie kan worden gecreëerd met de juiste I(t) en Q(t) basisbandsignalen (die op hun beurt de amplitudes variëren van de cosinus- en sinusgolven die samen worden gesommeerd).
Hetzelfde proces werkt natuurlijk omgekeerd om een RF-signaal te demoduleren. Door een RF-signaal te mengen met LO-signalen (lokale oscillator) in kwadratuur, kunnen I(t) en Q(t) basisbandsignalen worden gecreëerd.
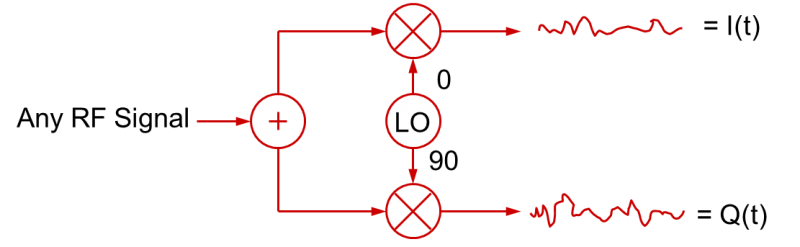
Dit is de fundamentele basis voor de meeste moderne RF-signaalgeneratie en -modulatie, alsook voor demodulatie en vectorsignaalanalyse.
Software Defined Radio (SDR)-systemen maken uitgebreid gebruik van deze concepten omdat de basisband I & Q-signalen vaak worden weergegeven als discrete, in de tijd bemonsterde gegevens. Daarom kan digitale signaalverwerking (DSP) worden gebruikt om de zender- en ontvangerkarakteristieken letterlijk te definiëren, met inbegrip van filtering, modulatie en demodulatie, AGC, enz. SDR-ontvangers hebben vaak een basisbandbandbreedte van enkele honderden kHz of meer, waardoor zij een grote verscheidenheid aan functies kunnen uitvoeren, waaronder “brede” bandscope- en spectrogramfuncties, alsmede de mogelijkheid om gelijktijdig meerdere signalen van verschillende typen te monitoren en te demoduleren.
Vectorsignaalgeneratoren hebben een kwadratuurmodulator die I(t)- en Q(t)-signalen accepteert, die vervolgens worden gebruikt voor amplitudemodulatie van een paar kwadratuursinusoïden die vervolgens worden opgeteld om de gemoduleerde RF-uitgang te creëren. Veel Vector Signal Generators hebben paneelaansluitingen waarop je je eigen IQ signalen kunt aansluiten. Vele hebben een interne baseband Arbitrary Waveform Generator (AWG) om de baseband IQ signalen te maken.
Moderne Vector Signal Analyzers hebben meestal bandbreedtes van 25, 40, 110MHz of meer. Zij zetten de inkomende RF signalen om in hun I en Q componenten. Alle analyses (spectrale analyse vs. tijd, demodulatie, pulsanalyse, enz.) zijn eenvoudigweg verschillende wiskundige bewerkingen op dezelfde IQ-gegevens. Real-Time Signal Analyzers, zoals de Tektronix RSA5000 en RSA6000 series, hebben de extra mogelijkheid om de “live” IQ gegevensstromen op te nemen en real-time verwerking van de gegevens uit te voeren. Dit voegt de mogelijkheid toe om dingen te doen zoals het live spectrum van een RF signaal visualiseren, alsmede de mogelijkheid om te triggeren op transiënte gebeurtenissen die alleen zichtbaar zijn in het frequentiedomein.
Zie Tektronix’s nieuwste spectrum analyzer aanbod.