Röntgendiffractie is een veelgebruikte materiaalkarakteriseringstechniek waarmee kristaloriëntaties en interatomaire spatiëring kunnen worden vastgesteld. Röntgenstralen worden hiervoor gebruikt omdat de golflengte op dezelfde lengteschaal ligt als de interatomaire afstand en de waarden van de roosterparameters.
Wat gebeurt er?
Een röntgenstraal wordt opgewekt in een vacuümbuis door een wolfraamdraad tot voorbij zijn werkfunctie te verhitten om elektronen uit te stoten. Vacuümomstandigheden zijn noodzakelijk om de gemiddelde vrije weg van de elektronen te vergroten. De elektronen worden versneld naar een koperen kathode met een energie in de orde van 25 keV. Botsingen van elektronen met de koperen kathode leiden tot ionisatie van de binnenste schil, waarbij röntgenstralen worden geproduceerd doordat elektronen met een hogere energie de lege ruimte met een lagere energie opvullen. Elektronen van verschillende hogere energieniveaus vallen naar beneden, waardoor elektromagnetische golven van verschillende energie worden geproduceerd. Aldus worden röntgenstralen van verschillende golflengten (van het type K-beta en K-alfa) opgewekt. Voor röntgendiffractie is het ideaal monochromatisch licht te hebben dat in wisselwerking staat met het monster, zodat de K-beta röntgenstralen worden uitgefilterd met een nikkelplaat. Hoewel er inderdaad twee geassocieerde K-alfa energieën zijn, zijn de energieën zo vergelijkbaar dat dit geen significante invloed heeft op het algemene piekprofiel. De röntgenstralen gaan door een collimator om de bundelbreedte aan te passen.
Een beetje achtergrond bij de wet van Bragg
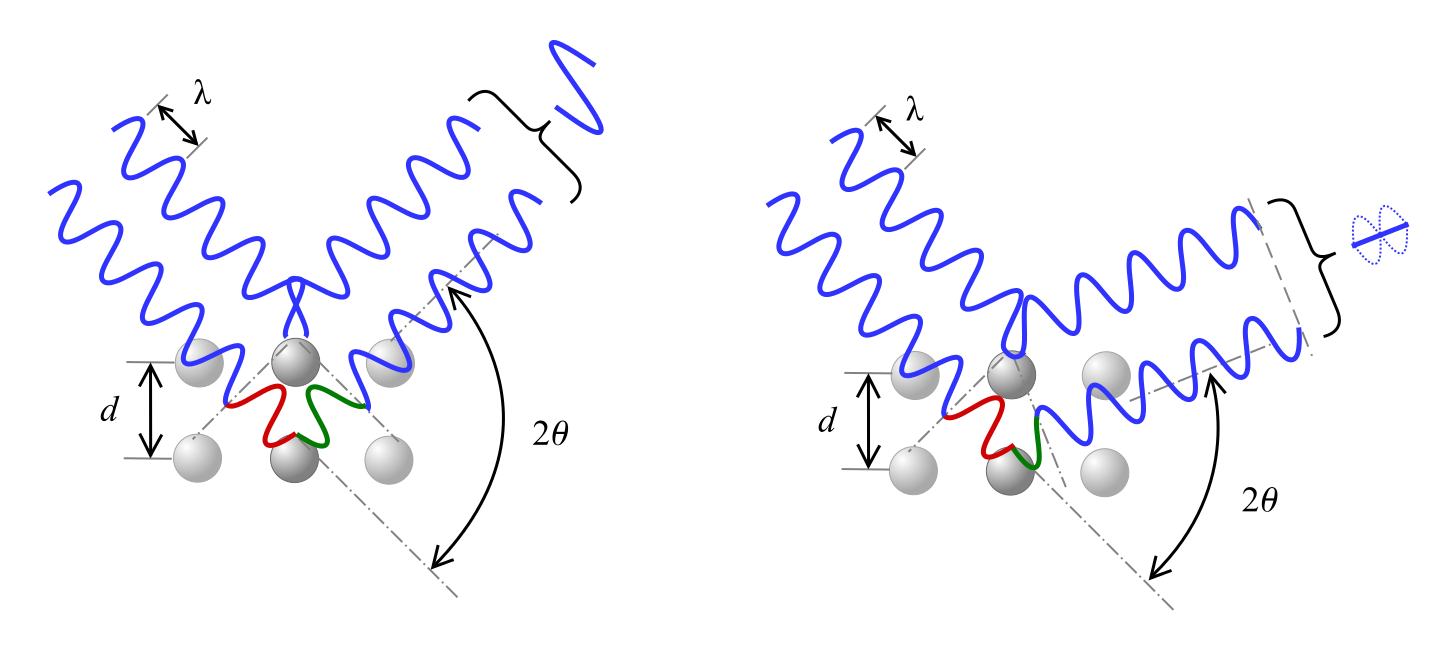
De wet van Bragg beschrijft de relatie voor constructieve interferentie, waarbij röntgenstralen met golflengte λ die onder een hoek θ op het materiaal vallen, worden afgebogen door kristalvlakken die gescheiden zijn door afstand d en waarbij n een geheel getal is.
Zoals hieronder te zien is, veroorzaakt een faseverschuiving in de golf ofwel constructieve interferentie, zoals links is afgebeeld, ofwel destructieve interferentie, zoals rechts is afgebeeld, afhankelijk van de hoek 2θ.
Vergelijkingen voor de interpretatie van XRD-resultaten
De teller, hieronder te zien in een schema van een röntgendiffractometer, wordt over een reeks van 2θ waarden gedraaid en registreert de intensiteit van het röntgensignaal dat op elke positie door het kristal wordt gereflecteerd. Deze intensiteit, gemeten als functie van 2θ, wordt gebruikt om een piekprofiel te genereren.
Voor hoeken die aan de Bragg-conditie voldoen, zal een piek in het röntgensignaal worden waargenomen als gevolg van de constructieve interferentie. Deze pieken worden vervolgens gebruikt om kristalrichtingen te identificeren en de roosterparameters te berekenen. Voor kubische systemen kan de interplanaire afstand, d, worden berekend met de volgende vergelijking die uit de kristalgeometrie wordt afgeleid, waarbij a de roosterparameter is en h, k en l de Miller-indices.
Combinatie van de wet van Bragg en de interplanaire afstand levert de volgende vergelijking op.
Hierbij hebben we alle constanten naar de linkerkant van de vergelijking verplaatst, zodat we de verhoudingen van sin2(θ)-waarden en Miller-indices tussen verschillende pieken kunnen vergelijken.
Wanneer de invallende elektromagnetische golf op het materiaal van het monster inslaat, worden de in het materiaal verblijvende elektronen in een oscillerend patroon gebracht, waardoor nieuwe röntgenstraling wordt opgewekt en de invallende lichtgolven effectief worden verstrooid. Er doen zich twee soorten verstrooiing voor: coherente of elastische verstrooiing, waarbij strak gebonden oscillerende elektronen röntgenstralen van dezelfde golflengte verstrooien, en incoherente verstrooiing, die optreedt wanneer los gebonden elektronen in een oscillerende beweging worden gebracht en röntgenstralen van verschillende energie genereren. Röntgendiffractie meet de intensiteit van coherent verstrooide röntgenstralen, die een piek vertonen waar de golven constructief interfereren. De atomaire verstrooiingsfactor kan worden gedefinieerd als de verhouding tussen de amplitude van de door een atoom verstrooide golf gedeeld door de amplitude van de door een enkel elektron verstrooide golf. Deze verhouding beschrijft in wezen de verstrooiingsefficiëntie van een atoom voor een bepaalde richting.
Voorbeeld van XRD-gegevens
Hier volgen de gegevens die zijn verzameld bij een experiment dat ik tijdens mijn bachelor-labcursus heb gedaan en waarbij ik heb geprobeerd een onbekend metaal te identificeren op basis van zijn kristalstructuur.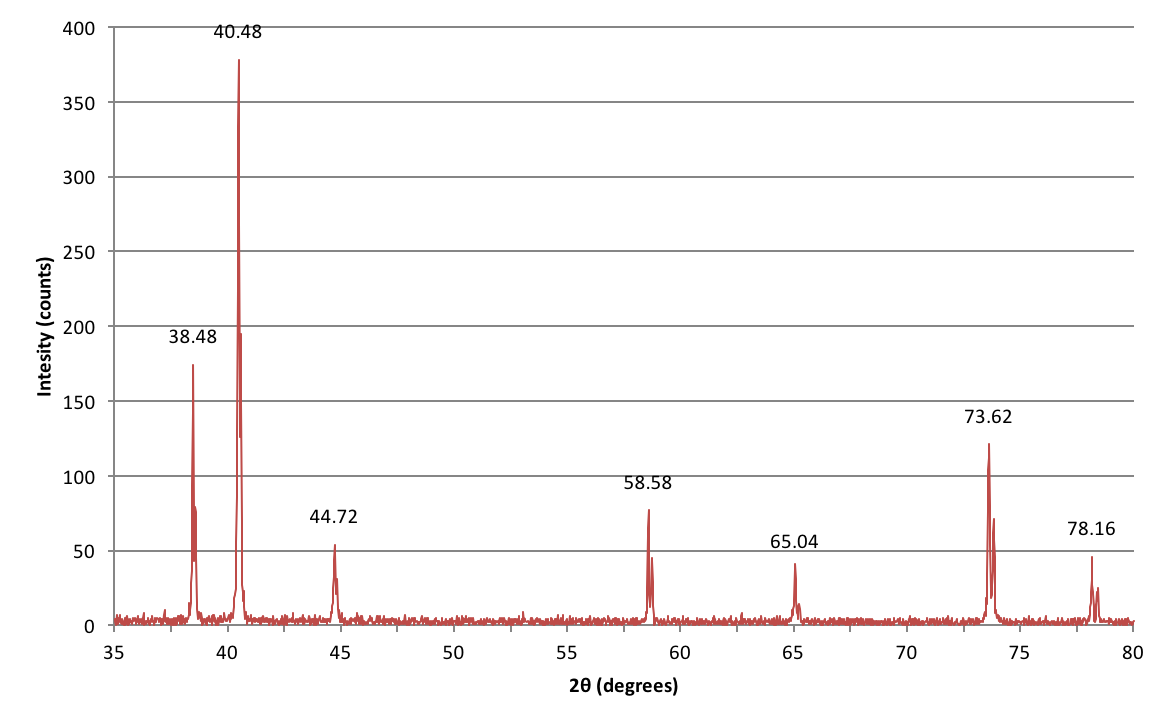
Hoe interpreteer ik deze pieken?
| Kristalstructuur | Voorwaarden |
|---|---|
| Simple Cubic | alle h, k, l-waarden |
| Gecentreerde kubus | h+k+l moet even zijn |
| Gecentreerde kubus | h, k, en l moeten allen even of oneven zijn |
Structuurfactoren houden rekening met gevallen waarin een vlak halverwege twee naburige vlakken kan liggen en destructieve interferentie kan veroorzaken. Deze factoren resulteren in een reeks regels voor verschillende kristalstructuurgeometrieën die bepalen wanneer constructieve interferentie kan optreden. In bovenstaande tabel staan de Miller index parameters waarbij constructieve interferentie zal optreden. Een uitgebreidere tabel staat hieronder. Door de verhoudingen van sin2θ (in de tweede tabel aangeduid als $Q^2$) voor verschillende diffractiepieken te vergelijken, kunnen de kristalstructuur en Miller-indexen worden bepaald.
| Kristalvlak (hkl) | $Q^2$ | Ruimtelatten waaruit reflecties mogelijk zijn | ||||
|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||
| 110 | 2 | SC | BCC | |||
| 111 | 3 | SC | FCC | DC | ||
| 200 | 4 | SC | BCC | FCC | ||
| 210 | 5 | SC | ||||
| 211 | 6 | SC | BCC | |||
| – | 7 | |||||
| 220 | 8 | SC | BCC | FCC | DC | |
| 300, 221 | 9 | SC | ||||
| 310 | 10 | SC | BCC | |||
| 311 | 11 | SC | FCC | DC | ||
| 222 | 12 | SC | BCC | FCC | ||
| 320 | 13 | SC | ||||
| 321 | 14 | SC | BCC | BCC | ||
| – | 15 | |||||
| 400 | 16 | SC | BCC | FCC | DC |
X-Stralingsdiffractie kent een breed scala van toepassingen voor materiaalkarakterisering. Het kan worden gebruikt als een experimentele methode om het volume van een eenheidscel experimenteel te bepalen voor theoretische dichtheidsberekeningen. Bovendien zal het vervormde rooster, indien het materiaal onder restspanning staat, een reeks van d-afstanden vertonen die voldoen aan de wet van Bragg, hetgeen resulteert in veel bredere diffractiepieken. De breedte van de diffractiepiek kan ook worden gebruikt om de grootte van de deeltjes te bepalen.