Introductie
In de informatica is een directed acyclic graph (DAG) een gerichte grafiek zonder cycli. In deze tutorial laten we zien hoe u een topologische sortering op een DAG in lineaire tijd kunt uitvoeren.
Topologische sortering
In veel toepassingen gebruiken we gerichte acyclische grafieken om de voorrang tussen gebeurtenissen aan te geven. Bijvoorbeeld, in een planningsprobleem is er een reeks taken en een reeks beperkingen die de volgorde van deze taken specificeren. We kunnen een DAG construeren om taken weer te geven. De gerichte randen van de DAG geven de volgorde van de taken weer.
Laten we eens kijken naar een probleem met hoe een persoon zich zou kunnen kleden voor een formele gelegenheid. We moeten verschillende kledingstukken aantrekken, zoals sokken, broeken, schoenen, enz. Sommige kledingstukken moeten voor de andere worden aangetrokken. Bijvoorbeeld, we moeten eerst sokken aantrekken en dan pas schoenen. Sommige kledingstukken kunnen in willekeurige volgorde worden aangetrokken, bijvoorbeeld sokken en broeken. We kunnen een DAG gebruiken om dit probleem te illustreren:
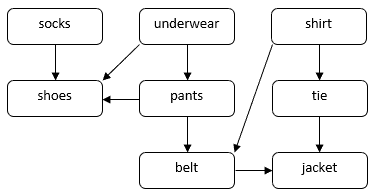
In deze DAG komen hoekpunten overeen met kledingstukken. Een directe rand 
in de DAG geeft aan dat we kledingstuk 
moeten aantrekken vóór kledingstuk 
. Onze taak is een volgorde te vinden voor het aantrekken van alle kledingstukken, met inachtneming van de afhankelijkheidsbeperkingen. We kunnen bijvoorbeeld kledingstukken in de volgende volgorde aantrekken:
Een topologische sortering van een DAG 
is een lineaire ordening van al zijn hoekpunten zodanig dat als een rand bevat, voor in de ordening staat. Voor een DAG kunnen we een topologische sortering construeren met een looptijd lineair met het aantal hoekpunten plus het aantal ribben, dat is 
.
Kahn’s Algoritme
In een DAG heeft elk pad tussen twee hoekpunten een eindige lengte omdat de grafiek geen cyclus bevat. Zij 
het langste pad van (bronvertex) naar (bestemmingsvertex). Omdat het langste pad is, kan er geen inkomende rand naar zijn. Een DAG bevat dus minstens één vertex dat geen inkomende edge heeft.
3.1. Algoritme van Kahn
In het algoritme van Kahn construeren we een topologische sortering op een DAG door hoekpunten te vinden die geen inkomende ribben hebben:
In dit algoritme berekenen we eerst de in-graadwaarden voor alle hoekpunten.
Daarna beginnen we met een hoekpunt waarvan de in-graad 0 is en plaatsen we het aan het eind van de uitvoerlijst. Zodra we een hoekpunt kiezen, werken we de in-graadwaarden van de aangrenzende hoekpunten bij, omdat het hoekpunt en zijn uitstaande randen uit de grafiek worden verwijderd.
We kunnen het bovenstaande proces herhalen totdat we alle hoekpunten hebben gekozen. De uitvoerlijst is dan een topologische sortering van de grafiek.
3.2. Tijdscomplexiteit
Om de in-graad van alle hoekpunten te berekenen, moeten we alle hoekpunten en ribben van bezoeken. Daarom is de looptijd voor in-graad berekeningen. Om te vermijden dat we deze waarden opnieuw moeten berekenen, kunnen we een array gebruiken om de in-graad waarden van deze hoekpunten bij te houden. Binnen de while lus moeten we ook alle hoekpunten en ribben bezoeken. Daarom is de totale looptijd .
Depth First Search
We kunnen ook een Depth First Search (DFS) algoritme gebruiken om de topologische sorter te construeren.
4.1. Grafiek DFS met recursie
Voordat we het aspect van de topologische sortering met DFS aanpakken, bekijken we eerst een standaard recursief algoritme voor het doorlopen van de grafiek DFS:
In het standaard DFS-algoritme beginnen we met een willekeurig hoekpunt in en markeren we dit hoekpunt als bezocht. Vervolgens roepen we recursief de functie dfsRecursive op om alle niet-bezochte aangrenzende hoekpunten te bezoeken. Op deze manier kunnen we alle hoekpunten van in tijd bezoeken.
Hoewel, omdat we elk hoekpunt onmiddellijk in de lijst zetten wanneer we het bezoeken, en omdat we bij elk hoekpunt kunnen beginnen, kan het standaard DFS algoritme niet garanderen dat het een topologisch gesorteerde lijst genereert.
Laten we eens kijken wat we moeten doen om deze tekortkoming aan te pakken.
4.2. DFS gebaseerd topologisch sorteeralgoritme
We kunnen het DFS-algoritme aanpassen om een topologische sortering van een DAG te genereren. Tijdens de DFS traversal, nadat alle buren van een hoekpunt zijn bezocht, zetten we het vooraan in de resultatenlijst 
. Op deze manier kunnen we ervoor zorgen dat voor al zijn buren in de gesorteerde lijst verschijnt:
Dit algoritme is vergelijkbaar met het standaard DFS algoritme. Hoewel we nog steeds beginnen met een willekeurig hoekpunt, zetten we het hoekpunt niet onmiddellijk in de lijst zodra we het bezoeken. In plaats daarvan bezoeken we eerst recursief al zijn buren en zetten het hoekpunt dan vooraan in de lijst. Dus, als een rand bevat, dan verschijnt voor in de lijst.
De totale looptijd is ook , want het heeft dezelfde tijdcomplexiteit als het DFS algoritme.
Conclusie
In dit artikel hebben we een voorbeeld laten zien van topologisch sorteren op een DAG. Ook hebben we twee algoritmen besproken die een topologische sortering kunnen maken in tijd.
De Java-implementatie van het op DFS gebaseerde topologische sorteeralgoritme is beschikbaar in ons artikel over Depth First Search in Java.