Posterior Probability & the Posterior Distribution

Probability > Posterior Probability & the Posterior Distribution

What is Posterior Probability?

Posterior waarschijnlijkheid is de waarschijnlijkheid dat een gebeurtenis zal plaatsvinden nadat met alle bewijzen of achtergrondinformatie rekening is gehouden. Het is nauw verwant aan de voorafgaande waarschijnlijkheid, die de waarschijnlijkheid is dat een gebeurtenis plaatsvindt voordat je rekening hebt gehouden met nieuw bewijsmateriaal. Je kunt de posterieure waarschijnlijkheid zien als een aanpassing op de prioriële waarschijnlijkheid:

Posterior waarschijnlijkheid = prior waarschijnlijkheid + nieuw bewijs (genaamd likelihood).
Bij voorbeeld, historische gegevens suggereren dat ongeveer 60% van de studenten die aan de universiteit beginnen, binnen 6 jaar zullen afstuderen. Dit is de waarschijnlijkheid vooraf. U denkt echter dat dit cijfer in werkelijkheid veel lager is, dus gaat u op zoek naar nieuwe gegevens. Het bewijs dat je verzamelt suggereert dat het werkelijke cijfer eigenlijk dichter bij 50% ligt; Dit is de posterior waarschijnlijkheid.

Oorsprong van de termen

De woorden posterior en prior komen van het Latijnse a priori. De definitie van “a priori” is:

“…betrekking hebbend op wat bekend kan worden door een begrip van hoe bepaalde dingen werken in plaats van door observatie” ~ Miriam Webster.

Het tegenovergestelde van “a priori” is “a posteriori”, dat wordt gedefinieerd als:

“…betrekking hebbend op wat bekend kan worden door observatie in plaats van door een begrip van hoe bepaalde dingen werken” ~ Miriam Webster.

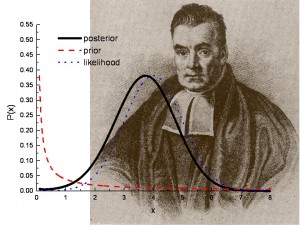
Wat is een posterieure verdeling?

De posterieure verdeling is een manier om samen te vatten wat we weten over onzekere grootheden in Bayesiaanse analyse. Het is een combinatie van de prioriteitsverdeling en de likelihood functie, die je vertelt welke informatie je waargenomen gegevens bevatten (het “nieuwe bewijs”). Met andere woorden, de posterior verdeling vat samen wat je weet nadat de gegevens zijn waargenomen. De samenvatting van het bewijs uit de nieuwe waarnemingen is de waarschijnlijkheidsfunctie.

Posterior Distributie = Prior Distributie + Likelihood Functie (“nieuw bewijs”)

Posterior verdelingen zijn van vitaal belang in Bayesiaanse Analyse. Zij zijn in vele opzichten het doel van de analyse en kunnen u:

• Intervalschattingen voor parameters,
• Puntschattingen voor parameters,
• Voorspellende gevolgtrekking voor toekomstige gegevens,
• Probabilistische evaluaties voor uw hypothese.

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!