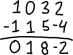Keer terug naar de Lessenindex | Doe de lessen in volgorde | Printvriendelijke pagina
Matrix Rij Bewerkingen (pagina 1 van 2)
“Bewerkingen” is wiskundigen-taal voor “procedures”. De vier “basisbewerkingen” van getallen zijn optellen, aftrekken, vermenigvuldigen en delen. Voor matrices zijn er drie basisbewerkingen op rijen; dat wil zeggen, er zijn drie procedures die je met de rijen van een matrix kunt uitvoeren.
De eerste bewerking is rij-omschakeling. Bijvoorbeeld, gegeven de matrix:

…kunt u de rijen omwisselen om de matrix in een mooiere rij-indeling te krijgen, zoals dit:
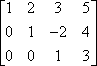
Rijen omwisselen wordt vaak aangegeven door pijlen te tekenen, zoals dit:

Bij het omwisselen van rijen moet u erop letten dat u de ingangen correct kopieert.
De tweede bewerking is rijvermenigvuldiging. Bijvoorbeeld, gegeven de volgende matrix:

…kunt u de eerste rij vermenigvuldigen met -1 om een positieve voorloopwaarde in de eerste rij te krijgen:
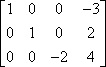
Deze rijvermenigvuldiging wordt vaak aangegeven met een pijl met de vermenigvuldiging erboven, zoals dit:
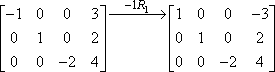
De “-1R1” geeft de eigenlijke bewerking aan. De “-1” geeft aan dat we vermenigvuldigd hebben met negatief 1; de “R1” geeft aan dat we met de eerste rij bezig waren. Merk op dat de tweede en derde rij ongewijzigd naar beneden gekopieerd zijn, naar de tweede matrix. De vermenigvuldiging gold alleen voor de eerste rij, dus de waarden voor de andere twee rijen werden gewoon ongewijzigd meegenomen.
Je kunt vermenigvuldigen met alles wat je maar wilt. Om bijvoorbeeld een leidende 1 in de derde rij van de vorige matrix te krijgen, kunt u de derde rij vermenigvuldigen met een negatieve helft:

Omdat u niets met de eerste en tweede rij deed, werden die gegevens gewoon ongewijzigd gekopieerd naar de nieuwe matrix.
Je kunt meer dan één rijvermenigvuldiging binnen dezelfde stap doen, dus je had de twee bovenstaande stappen ook in één stap kunnen doen, zoals dit:
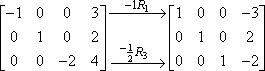
Het is een goed idee om een vorm van notatie te gebruiken (zoals de pijlen en subscripts hierboven), zodat je je werk kunt bijhouden. Matrices zijn erg rommelig, vooral als je ze met de hand maakt, en notities kunnen het makkelijker maken om je werk later te controleren. Het zal ook indruk maken op je leraar.
De laatste rij bewerking is rij optelling. Rij optellen is vergelijkbaar met de “addition” methode voor het oplossen van stelsels lineaire vergelijkingen. Stel je hebt het volgende stelsel vergelijkingen:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Aanvulling
Je zou kunnen beginnen met het oplossen van dit stelsel door de kolommen op te tellen om 4y = 4 te krijgen:
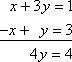
Je kunt iets soortgelijks doen met matrices.Bijvoorbeeld, gegeven de volgende matrix:

…kunt u de tweede rij “verkleinen” (meer voorloopnullen krijgen) door de eerste rij eraan toe te voegen (het algemene doel met matrices in dit stadium is om een “1” – of “0’s” en dan een “1” – aan het begin van elke matrixrij te krijgen). Toen je het lineaire stelsel van twee vergelijkingen verkleinde door op te tellen, trok je een “gelijken”-balk over de bodem en telde je naar beneden op. Als je optellen gebruikt bij een matrix, dan moet je wat kladpapier pakken, want je wilt niet proberen het werk binnen de matrix te doen. Dus tel de twee rijen op je kladpapier op:
|
Krabbelwerk – |
|
Dit is je nieuwe tweede rij; je schrijft hem op de plaats van de oude tweede rij. Het resultaat ziet er dan zo uit:
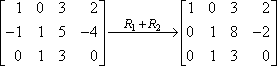
In dit geval betekent de “R1 + R2” op de pijl “Ik heb rij één bij rij twee opgeteld, en dit is het resultaat dat ik kreeg”. Omdat rij één niet echt veranderd is, en omdat we niets met rij drie gedaan hebben, worden deze rijen ongewijzigd in de nieuwe matrix gekopieerd.
Top | 1 | 2 | Return to Index Next >>
|
Citeer dit artikel als: |
Stapel, Elizabeth. “Matrix rij operaties.” Purplemath. Beschikbaar via 2016
|