Classificatie door discriminantanalyse
Laten we eens zien hoe LDA kan worden afgeleid als een classificatiemethode onder supervisie. Beschouw een algemeen classificatieprobleem: Een willekeurige variabele X komt uit een van K klassen, met enkele klasse-specifieke waarschijnlijkheidsdichtheden f(x). Een discriminantregel probeert de dataruimte te verdelen in K disjuncte regio’s die alle klassen vertegenwoordigen (stel je de vakjes op een schaakbord voor). Met deze regio’s betekent classificatie door discriminantanalyse eenvoudigweg dat we x aan klasse j toewijzen als x in regio j ligt. De vraag is dan, hoe weten we in welke regio de gegevens x vallen? Uiteraard kunnen we twee toewijzingsregels volgen:
- Maximale waarschijnlijkheidsregel: Als we aannemen dat elke klasse met evenveel waarschijnlijkheid kan voorkomen, wijzen we x toe aan klasse j als

- Bayesiaanse regel: Als we de klasse-prioriteiten, π, kennen, dan x aan klasse j toewijzen als

Lineaire en kwadratische discriminantanalyse
Als we aannemen dat de gegevens afkomstig zijn van een multivariate Gaussische verdeling, d. w. z.d.w.z. dat de verdeling van X kan worden gekarakteriseerd door zijn gemiddelde (μ) en covariantie (Σ), kunnen expliciete vormen van de bovenstaande toewijzingsregels worden verkregen. Volgens de Bayesiaanse regel delen wij de gegevens x in klasse j in, indien zij van alle K klassen voor i = 1,…,K de hoogste waarschijnlijkheid heeft:

De bovenstaande functie wordt de discriminantiefunctie genoemd. Let op het gebruik van log-likelihood hier. Met andere woorden, de discriminantfunctie vertelt ons hoe waarschijnlijk gegevens x uit elke klasse zijn. De beslissingsgrens die twee klassen, k en l, scheidt, is dus de verzameling x waarbij twee discriminantfuncties dezelfde waarde hebben. Daarom is elk gegeven dat op de beslissingsgrens valt even waarschijnlijk uit de twee klassen (we konden niet beslissen).
LDA ontstaat in het geval waarin we uitgaan van gelijke covariantie tussen K klassen. Dat wil zeggen, in plaats van één covariantiematrix per klasse, hebben alle klassen dezelfde covariantiematrix. Dan krijgen we de volgende discriminantfunctie:

Merk op dat dit een lineaire functie is in x. De beslissingsgrens tussen elk paar klassen is dus ook een lineaire functie in x, de reden voor de naam: lineaire discriminantanalyse. Zonder de aanname van gelijke covariantie vervalt de kwadratische term in de waarschijnlijkheid niet, zodat de resulterende discriminantfunctie een kwadratische functie in x is:

In dit geval is de beslissingsgrens kwadratisch in x. Dit staat bekend als kwadratische discriminantanalyse (QDA).
Wat is beter? LDA of QDA?
In echte problemen zijn populatieparameters meestal onbekend en worden ze geschat uit de trainingsgegevens als de steekproefgemiddelden en steekproefcovariantiematrices. Hoewel QDA in vergelijking met LDA flexibeler beslissingsgrenzen toestaat, neemt het aantal te schatten parameters ook sneller toe dan bij LDA. Voor LDA zijn (p+1) parameters nodig om de discriminantfunctie in (2) te construeren. Voor een probleem met K klassen zouden we slechts (K-1) dergelijke discriminantfuncties nodig hebben door willekeurig één klasse als basisklasse te kiezen (door de waarschijnlijkheid van de basisklasse af te trekken van alle andere klassen). Het totale aantal geschatte parameters voor LDA is dus (K-1)(p+1).
Anderzijds moeten voor elke QDA-discriminantfunctie in (3) de gemiddelde vector, de covariantiematrix en de klassevoorkeur worden geschat:
– Gemiddelde: p
– Covariantie: p(p+1)/2
– Klasse-prioriteit: 1
Zo ook moeten we voor QDA (K-1){p(p+3)/2+1} parameters schatten.
Daarom neemt het aantal geschatte parameters in LDA lineair toe met p, terwijl dat van QDA kwadratisch toeneemt met p. We zouden verwachten dat QDA slechter presteert dan LDA wanneer de probleemdimensie groot is.
Best van twee werelden? Compromis tussen LDA & QDA
We kunnen een compromis vinden tussen LDA en QDA door de individuele klasse covariantie matrices te regulariseren. Regularisatie betekent dat we een bepaalde restrictie op de geschatte parameters leggen. In dit geval vereisen we dat de individuele covariantiematrix krimpt tot een gemeenschappelijke gepoolde covariantiematrix via een strafparameter, bv. α:

De gemeenschappelijke covariantiematrix kan ook worden geregulariseerd in de richting van een identiteitsmatrix via een strafparameter, bv, β:

In situaties waarin het aantal inputvariabelen veel groter is dan het aantal steekproeven, kan de covariantiematrix slecht worden geschat. Inkrimping kan hopelijk de nauwkeurigheid van de schatting en de classificatie verbeteren. Dit wordt geïllustreerd door onderstaande figuur.

Berekening voor LDA
Uit (2) en (3) kunnen we afleiden dat berekeningen van discriminantfuncties kunnen worden vereenvoudigd als we eerst de covariantiematrices diagonaliseren. Dat wil zeggen, de gegevens worden getransformeerd zodat ze een identieke covariantiematrix hebben (geen correlatie, variantie van 1). In het geval van LDA gaan we als volgt te werk:

Stap 2 verdeelt de gegevens om een identieke covariantiematrix in de getransformeerde ruimte te verkrijgen. Stap 4 wordt verkregen door (2) te volgen.
Laten we een tweeklassenvoorbeeld nemen om te zien wat LDA werkelijk doet. Stel dat er twee klassen zijn, k en l. We delen x in bij klasse k als

De bovenstaande voorwaarde betekent dat klasse k een grotere kans heeft om gegevens x te produceren dan klasse l. Als we de vier hierboven beschreven stappen volgen, schrijven we
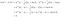
Dat wil zeggen, we delen gegevens x in bij klasse k als

De afgeleide toewijzingsregel onthult de werking van LDA. Het linkerlid (l.h.s.) van de vergelijking is de lengte van de orthogonale projectie van x* op het lijnstuk dat de twee klassegemiddelden verbindt. Het rechterdeel is de plaats van het middelpunt van het segment, gecorrigeerd met de klassevoorspellingen. In wezen classificeert LDA de gesferde gegevens naar het dichtstbijzijnde klassegemiddelde. Hierover kunnen we twee opmerkingen maken:
- Het beslissingspunt wijkt af van het middelpunt wanneer de klasse-voorspellingen niet gelijk zijn, d.w.z. de grens wordt opgeschoven naar de klasse met een kleinere voorwaarschijnlijkheid.
- De gegevens worden geprojecteerd op de ruimte die door de klasse-gemiddelden wordt opgespannen (de vermenigvuldiging van x* en de aftrekking van het gemiddelde op de l.h.s. van de regel). Afstandsvergelijkingen worden dan in die ruimte uitgevoerd.