How Many Sides Does A Circle Have?

Het is een huiswerkvraag van de lagere school die onenigheid veroorzaakt onder doorgewinterde wiskundigen. Om het juiste antwoord te vinden, heb ik een beroep gedaan op het meest rigoureuze van de wetenschappelijke instrumenten, de Twitter poll:

In retrospect betreur ik het dat ik geen “geen van bovenstaande” optie heb opgenomen, maar daarover later meer. In dit bericht zal ik deze drie antwoorden (en “Geen van bovenstaande”) doorlopen, en hun voor- en nadelen bespreken zoals ik ze zie, voordat ik op dramatische wijze het juiste antwoord onthul.

Maar eerst: waarom kunnen we niet rechttoe rechtaan het juiste antwoord geven? De woorden in de vraag zijn nauwelijks mysterieus. We weten allemaal wat een “cirkel” is, wat het betekent om “hoeveel” van iets te tellen, en wat een “zijde” is… of toch niet? Hier zijn (ruwe) definities die ik distilleerde uit gesprekken met twee leerlingen van de lagere school die deze vraag hadden gekregen:

1. Een lijn die deel uitmaakt van de begrenzing van een vorm van een vlakke figuur.

De bedoeling van het zeggen van vlakke figuur in plaats van “vorm” hier is dat we vormen willen die leven in 2-dimensies (bijvoorbeeld vierkanten of cirkels, maar geen bollen of kubussen). De volgende vraag is wat een “lijn” is in definitie 1. Hier is een variant die dat vastlegt:

2. Een rechte lijn die deel uitmaakt van de grens van een vlakke figuur.

Als u “define: side” intypt in Google, is de meest relevante definitie:

Een rechtlijnige figuur is een uit rechte lijnen opgebouwde figuur. Deze definitie is dus een verdere verfijning van definitie 2, en stelt ons in staat te bevestigen dat een vierkant vier zijden heeft, maar zegt op het eerste gezicht niets over niet-rechtlijnige vlakke figuren zoals cirkels.

Eindig veel zijden?

Ik denk dat het een veilige gok is dat de respondenten van mijn Twitter-peiling een hoger niveau van wiskundige scholing hebben dan het nationale gemiddelde. Het feit dat ze überhaupt verdeeld waren over deze vraag, en dat een kleine meerderheid een antwoord koos dat voor het gebruikelijke publiek van deze vraag (basisschoolleerlingen) vrijwel onbereikbaar is, wijst er zeker op dat er ergens iets mis gaat.

Zo, heeft een cirkel oneindig veel zijden? Het is zeker nuttig om een cirkel te beschouwen als de limiet van n-hoekige veelhoeken naarmate n groter en groter wordt. Dit is precies de benadering die Archimedes, Liu Hui en talloze anderen door de eeuwen heen hebben gebruikt om cirkelmeetkunde te bestuderen, inclusief benaderingen voor π.

Een 16e-eeuwse uitgave uit de Ming-dynastie van de Jiuzhang suanshu (Negen hoofdstukken over de wiskundige kunst), derde eeuw n.Chr.

Soms is het absoluut zinnig, als handige steno, om een cirkel te zien als een veelhoek met oneindig veel zijden.

Maar, als onuitstaanbaar pedant wiskundige, zou ik onderscheid willen maken tussen handige steno en letterlijke waarheid. Als we er op staan dat een cirkel werkelijk een veelhoek is met oneindig veel zijden, dan rijst de vraag: wat zijn de zijden? En het enige plausibele antwoord is: de afzonderlijke punten van de cirkel. Hoe lang zijn die zogenaamde zijden? Nul centimeter. En zijn deze zijden gescheiden door hoeken? Blijkbaar niet, of er zijn helemaal geen hoeken, of elk punt is zowel een zijde als een hoek.

Ik zou zeggen dat zijden van lengte nul… een problematisch concept zijn. Hoe weet je of je ze hebt? Stel bijvoorbeeld dat ik een stelsel bestudeer waarin een vierkant ontstaat als een limiet van achthoeken zoals deze:

In deze situatie zou het voor mij heel logisch kunnen zijn om te denken dat mijn vierkant acht zijden heeft, waarvan er vier lengte nul hebben. Maar als ik zou volhouden dat mijn (doodgewone) vierkant echt acht zijden heeft, zou u misschien uw wenkbrauwen optrekken.

Dus dit – het winnende antwoord in mijn poll – is het enige antwoord dat ik definitief fout ga verklaren, terwijl het ook het enige antwoord is dat enig meetkundig inzicht biedt. Een paradox? Niet echt. Redeneren naar analogie is een waardevolle vaardigheid in de wiskunde en in het leven; tegelijkertijd is het belangrijk om vast te houden aan het besef dat dat is wat we doen.

Voor oneindig veel zijden: meetkundig verhelderend.
Tegen oneindig veel zijden: achtzijdige vierkanten.

Off on a tangent 1: apeirogonen

Zelfs als een cirkel er geen is, zijn er dan zoiets als veelhoeken met oneindig veel zijden? Nou, er is een woord om zoiets te beschrijven een apeirogon. Een regelmatige apeirogon zou dan zijden hebben van gelijke (niet nul) lengte met gelijke hoeken ertussen. De enige optie hier is dit verbijsterend onaantrekkelijke object:

Als u er bezwaar tegen heeft dat dit een “veelhoek” is (hetzij vanwege de hoeken van 180°, hetzij vanwege de keten van randen die niet in een lus sluiten), wat dacht u dan van iets als dit: begin onderaan een cirkel, en beweeg in elk stadium rond de helft van wat er van de cirkel overblijft, en vervang de boog die je net hebt afgelegd door een rechte rand:

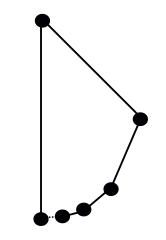
Is dit een echte veelhoek? Nogmaals, dat hangt af van wat je bedoelt. Volgens één gangbare definitie, die van een “gesloten veelhoekige keten”, voldoet deze niet, omdat de starthoek (linksonder) slechts met één rand verbonden is. Maar het scheelt niet veel: dat punt is de limiet van een reeks ribben van rechts, waardoor deze vorm een “niet-zelfdoorsnijdende stukgewijs lineaire gesloten kromme” is, een andere definitie van veelhoek die mensen gebruiken.

Als we onze gebruikelijke euclidische wereld verlaten en de hyperbolische ruimte binnengaan, dan is er geen dubbelzinnigheid. Apeirogonen (zelfs regelmatige apeirogonen) bestaan gewoon:

Een betegeling van het hyperbolische vlak door regelmatige apeirogonen. (Door Anton Sherwood – Eigen werk, Publiek Domein, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extreme punten

Het is misschien beter te verdedigen dat een cirkel oneindig veel hoeken heeft dan oneindig veel zijden (hoewel dit niet een vraag is die erg vaak gesteld lijkt te worden). Om te beginnen, als een hoek van een vierkant een punt is waar de grenslijn niet recht is, dan voldoet elk punt op de cirkel daaraan. Meer gesofisticeerd bestaat er een notie van een extreem punt van een vorm: dat is elk punt waardoor men een lijnstuk kan trekken dat de vorm alleen in dat punt raakt. Voor een vierkant en veel bekende vormen vallen de extreme punten precies samen met de hoeken. Elk punt op de grens van de cirkel is een extreem punt, dus het is zeker waar dat een cirkel er oneindig veel heeft.

We zouden ons zorgen kunnen maken dat sommige vormen, zoals deze chevron, hoeken hebben die geen extreme punten zijn:

Hier is de onderste centrale hoek geen extreem punt (de andere drie hoeken wel). Wat er mis gaat is dat deze vorm niet convex is (ruwweg, er steken stukjes te ver uit). Een cirkel is convex, dus misschien hoeven we ons geen zorgen te maken. Als alternatief kunnen we de situatie oplossen door een “hoek” te definiëren als een punt dat een extreem punt is van de vorm in kwestie of van zijn complement, d.w.z. het hele vlak met de vorm er uit gesneden. Op die manier zouden hoeken van alle veelhoeken, met inbegrip van de chevron, kunnen worden opgespoord. Voor gladde krommen zouden alle grenspunten als “hoeken” worden aangemerkt, behalve buigpunten (wat niet onredelijk is, want daar is de grens recht).

Een zijde?

Op de lagere school schijnt “een” het antwoord te zijn dat een vinkje krijgt. En er is een matig fatsoenlijke rechtvaardiging voor. Denk aan definitie 1 hierboven:

1. Een lijn die deel uitmaakt van de begrenzing van een vlakke figuur.

De onmiddellijke vraag is wat telt als een “lijn”, vooral als we niet aandringen op rechtheid. Als we hier te soepel mee omgaan, dan zou van elke vlakke figuur gezegd kunnen worden dat hij “een zijde” heeft, in dezelfde zin als dat hij een grens, omtrek of omtrek heeft. Maar dit moet verkeerd zijn, want we willen toch zeker dat een vierkant er vier heeft. Welnu, een vierkant heeft vier punten waar het niet glad is, met daartussen vier gladde gedeelten. Misschien waren het eigenlijk de gladde delen die we al die tijd telden. Dus impliciet hebben we een nieuwe verfijning van definitie 1 (en maken we van de gelegenheid gebruik om de vage term “figuur” te schrappen):

4. Elke gladde doorsnede van een stukgewijs-gladde gesloten kromme.

Een “gesloten kromme” is een kromme die in een lus om zichzelf heen gaat, zodat zij geen vrije einden heeft. “Stuksgewijs-smooth” betekent dat de kromme is opgebouwd uit gladde doorsneden, die elkaar ontmoeten in geïsoleerde oneffen punten. Het is volkomen legitiem om de gladde delen van de grens van zo’n vorm te willen tellen, en het is geenszins schandalig om daarvoor het woord “zijde” te gebruiken. Ik zeg dus zeker niet dat dit definitief het verkeerde antwoord is.

De vraag is of die interpretatie van “zijde” niet alleen coherent is, maar ook natuurlijk genoeg dat ze gewoon kan worden aangenomen zonder expliciet te worden vermeld (wat zelden of nooit het geval is). Wat gebeurt er als gladheid en rechtheid op verschillende manieren samenvallen? Beschouw deze grafsteenvorm, gemaakt door de top van een vierkant te vervangen door een halve cirkel van gelijke diameter.

Deze heeft twee gladde delen (de onderste lijn en de rest) maar drie rechte randen (plus een gebogen stuk dat twee van die randen glad verbindt). Dus hoeveel zijden heeft het? Ik heb mijn Twittervrienden weer geraadpleegd:

Deze keer had ik “oneindig veel” als optie moeten opnemen, hoewel dat kan worden opgevangen in “Geen van bovenstaande”. Iedereen die stemt dat de cirkel oneindig veel zijden heeft, zou hier automatisch “Geen van bovenstaande” moeten stemmen, tenzij – een belangrijk voorbehoud – de aard van deze vorm de lezer een andere notie van “zijde” geeft. Het feit dat de populairste keuzes in deze twee peilingen onverenigbaar zijn, suggereert dat dit het geval zou kunnen zijn (of versterkt op zijn minst dat de wateren troebel zijn).

Hoewel twee een volkomen respectabel antwoord is, verenigbaar met definitie 4 hierboven en met de eenzijdigheid van een cirkel, ben ik er niet van overtuigd dat het definitief het juiste antwoord is, of dat drie of vier categorisch verkeerd zijn. Het hangt ervan af wat je wilt tellen: gladde doorsneden, rechte randen, of rechte randen plus wat er dan nog overblijft, en elk van die antwoorden kan het antwoord zijn dat je wilt, afhankelijk van de context (meer hierover hieronder). Ik ben er niet zeker van dat het tellen van het aantal gladde gedeelten volledig overeenkomt met mijn intuïtie van het woord “zijde”. Immers, de twee rechtopstaande delen van de zerk zijn – ik denk dat het redelijk is te zeggen – “aan tegenovergestelde zijden”. Zijn we er echt tevreden mee dat ze tegelijkertijd deel uitmaken van “dezelfde zijde”?

Je zou kunnen tegenwerpen dat ik twee verschillende betekenissen van “zijde” door elkaar haal, dat terminologie soms botst, en dat we er maar mee moeten leren leven. Ik ben daar echter niet zo zeker van. De bedoeling van deze oefening is om te extrapoleren vanuit een situatie (rechtlijnige figuren) waarin de twee begrippen vrij goed samengaan. Als er een nieuw idee was dat alles bevatte wat we goed vonden aan het origineel, maar dat ook van toepassing was op een bredere categorie van vormen, dan zou dat een overweldigende claim hebben om het enige juiste antwoord te zijn. Maar als al onze pogingen tot veralgemening inhouden dat we wenselijke aspecten van het origineel opofferen, dan is er misschien niet één juiste veralgemening. Er zijn verschillende keuzes, met verschillende afwegingen, die in verschillende contexten geschikt zouden kunnen zijn (en als we in een situatie verkeren waarin er meer dan één in het spel is, dan zouden we die verschillende namen kunnen geven).

Hier is nog een variatie: een grafsteen van Weierstrass, gemaakt door de bovenrand van een vierkant te vervangen door een doorsnede van de Weiestress-functie, een oneindig kronkelige lijn die nergens glad is.

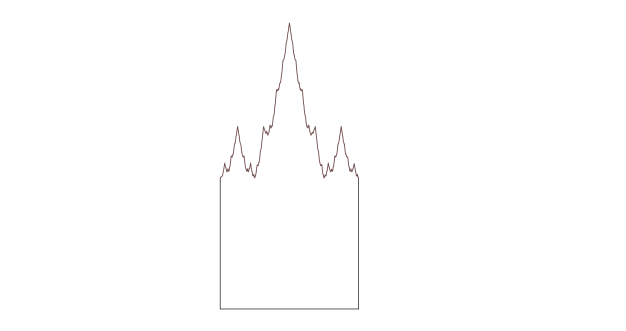
Hier (en let op de typefout) wat mijn Twitter-vrienden hiervan vonden – hoewel er minder waren die hun mening gaven:

Ondanks de scepsis van mijn Twitter-volgers zal ik zo uitleggen waarom ik het niet gek vind om dit te zien als een vierkant met vier zijden (waarvan er één niet glad is). Aan de andere kant, als je liever je zijden glad hebt, dan heb je weer de keuze tussen zien dat het oneindig veel zijden heeft (waarvan er drie lengte 1 hebben, en de rest lengte 0), of dat het 3 zijden heeft plus een stuk van zeker-niet-een-zijde grens.

Voor een zijde: een enkele vloeiende kromme.
Tegen een zijde: dezelfde zijde aan tegenoverliggende zijden.

Off on a tangent 3: zijden versus randen

Hoeveel zijden heeft een vierkant? Vier. Hoeveel ribben heeft een vierkant? Vier. Zijn kanten en zijden dan hetzelfde? Niet noodzakelijkerwijs. Hier zijn twee configuraties die – op zijn minst aannemelijk – elk vierzijdig zijn, maar respectievelijk 5 en 3 ribben hebben:

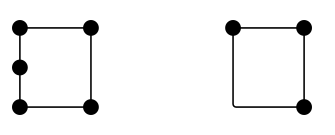
In het algemeen, zou ik zeggen, is een “rand” een topologisch object, in die zin dat zijn functie, niet zijn vorm, van belang is. Denk maar aan de plattegrond van de Londense metro. Als je vraagt hoeveel randen er in dat netwerk zijn, is het niet zinvol om rechte of gladde stukken op te tellen. Het zijn de verbindingen tussen de stations (of hoekpunten) die tellen.

Zoals reeds gezegd, is het gebruikelijk om aan een veelhoek te denken als een zeer eenvoudig soort netwerk dat een gesloten veelhoekige keten wordt genoemd: een reeks hoekpunten (in dit geval de hoeken van de veelhoek), verbonden met ribben, zodanig dat elk hoekpunt aan precies twee ribben ligt, en het geheel een enkele lus vormt. In deze situatie vallen ribben en zijden samen, evenals hoekpunten en hoeken. Maar in het algemeen kun je deze samenloop doorbreken, zoals in de twee kleine netwerken hierboven.

Als je netwerk-theoretisch over dingen wilt nadenken, maar de hoekpunten zijn niet duidelijk aangegeven, dan moet je raden waar ze zitten. Bij een veelhoek is dat gemakkelijk – de hoekpunten liggen op de hoeken – en daarom is het omschakelen tussen geometrische en topologische benaderingen zo natuurlijk. Maar bij andere vormen, zoals een van de grafstenen hierboven, is dat misschien niet zo vanzelfsprekend. Niettemin, in elk van deze gevallen, als men u zou zeggen dat er ergens hoekpunten zijn, en u zou vragen ze te lokaliseren, dan denk ik dat het verstandig zou zijn te raden dat het er vier zijn, namelijk de hoeken van het oorspronkelijke vierkant, en dat de bovenste rand om de een of andere reden is voorgesteld als een niet-rechte lijn. En als we er op die manier over willen denken, met elk van de grafstenen met 4 randen, dan lijkt het misschien vreemd (hoewel logisch samenhangend!) om vol te houden dat ze een ander aantal zijden hebben (vooral omdat de bovenste zijde – ondanks zijn eigen geometrie – duidelijk “aan één kant” van de figuur ligt). In plaats van te gissen, vroeg een van mijn Twitter-correspondenten me: “Zijn beide bovenste hoekpunten verwijderd?”, een vraag die alleen zin heeft vanuit een netwerktheoretisch perspectief.

Waar laat dit de cirkel? Het probleem is dat geen enkel punt op de cirkel een betere aanspraak heeft om hoekpunt te zijn dan enig ander. Dus hoewel het verleidelijk is (en ook weer coherent) om een cirkel te zien als een netwerk met één rand, is er, als we er hoekpunten in gaan opnemen, geen duidelijke reden om er één te verkiezen boven een ander aantal.

Zouden we het kunnen zien als een netwerk zonder hoekpunten, een soort metrolijn zonder stations? De gebruikelijke wiskundige opvatting van een netwerk zou dat niet toelaten, maar dat mag ons niet te veel afschrikken. Dit suggereert een zuiver topologische benadering. Het probleem is dat vanuit dat gezichtspunt een cirkel een soort netwerk kan zijn zonder hoekpunten en met één rand, maar dat een vierkant dat ook is (als de metro toevallig zo is aangelegd). In de topologie is een vierkant een cirkel. (Dit is geen paradox, het zegt alleen dat de grens een enkele lus is, waarvan de vorm er niet toe doet). Dus terwijl dit soort netwerk “één rand” heeft, heeft een vierkant natuurlijk niet “één zijde”, dus de relatie tussen zijden (meetkundig) en randen (topologisch) is weer verbroken, net zoals in de twee kleine netwerken hierboven. Dus deze benadering brengt ons niet erg ver.

Geen zijden?

Het lijkt misschien paradoxaal om te stellen dat een cirkel (of welke vorm dan ook) “geen zijden” heeft. Maar het argument voor de verdediging is rechttoe rechtaan. We keren terug naar definitie 2:

2. Een rechte lijn die deel uitmaakt van de begrenzing van een vlakke figuur.

Dit is een eenvoudige, gemakkelijk te begrijpen uitdrukking die perfect de zijden van een vierkant weergeeft. We zijn er niet in geslaagd een bevredigende veralgemening hiervan te vinden voor gekromde figuren, dus het beste is om bij het origineel te blijven. En een cirkel heeft er geen.

Voor geen zijden: waar, volgens een zinnige opvatting van “zijde”.
Tegen geen zijden: klinkt als een Zen koan.

None of the Above?

Herhaal de definitie van Google:

3. Elk van de lijnen die de begrenzing vormen van een vlakke rechtlijnige figuur.

Probeert men dit toe te passen op een cirkel – een niet-rechtlijnige figuur – levert niets op. De vraag is net zo zinloos als “Hoeveel zijden heeft maandag?”

Sinds definitie 3 de meest officiële is (de enige in dit bericht die niet door mij of mijn kinderen is verzonnen), maakt dat dan niet “Geen van bovenstaande” categorisch tot het juiste antwoord? Misschien. Aan de andere kant: als iemand ons een vraag stelt, vereist het principe van de naastenliefde misschien dat we aannemen dat die vraag zinvol is, tenzij we het tegendeel met zekerheid kunnen vaststellen, en de definities 1, 2, 4 en andere varianten maken dat mogelijk. Verder is definitie 3 eerder taalkundig dan formeel wiskundig, en dus eerder beschrijvend dan voorschrijvend, zodat we er niet door verstrikt moeten raken.

Voor geen van bovenstaande: semantisch defect.
Tegen geen van bovenstaande: dialogische naastenliefde.

Het juiste antwoord

Wat heeft me ertoe aangezet dit bericht te schrijven? Zoals ontelbare leerlingen van de lagere school, werd deze vraag onlangs aan mijn vijfjarige tweelingzonen – de leerlingen van de lagere school waarover ik het in het begin had – gesteld bij hun huiswerk. De ene koos voor “1” en de andere voor “0”, en ik heb geprobeerd hun redenering hierboven vast te leggen en uit te breiden. Ik denk dat beide antwoorden heel goed te verdedigen zijn – en geen van beide is definitief juist.

Dus, wat moet je doen als je de vraag wordt gesteld: Hoeveel zijden heeft een cirkel? Volgens mij is het beste antwoord dat je de wiskundige in je leven vraagt een verhandeling van 3000 woorden over het onderwerp te schrijven, die je dan kunt uitprinten en triomfantelijk aan je ongelukkige leraar kunt overhandigen. Maar als dat niet lukt, is de beste aanpak het voorbeeld van Socrates te volgen en de vraag met een wedervraag te beantwoorden: Wat bedoelt u met “kant”?

Tellen tot nul, of tot één, of weigeren de vraag te beantwoorden, zegt ons uiteindelijk vrijwel niets over de meetkunde van cirkels. Maar er valt veel te winnen door vertrouwde begrippen uit elkaar te halen, door extra voorwaarden te laten vallen of toe te voegen, door onze intuïtie uit te dagen door van de ene context naar een iets andere te gaan, en door te proberen precies op te schrijven wat we bedoelen met een bepaalde term in een bepaalde setting. Dat is waar het in de echte wiskunde om gaat.

Footnotes

Je zou ook iets anders kunnen doen: bijvoorbeeld een beginpunt P op de cirkel kiezen, van waaruit de afstand rond de omtrek wordt gemeten. Verklaar dan dat de punten op rationale afstand van P hoeken zijn en de rest zijden. Dit levert een telbaar oneindig aantal hoeken op en een ontelbaar oneindig aantal zijden. Of men zou het omgekeerde kunnen beweren. Dit zou goed passen bij de veelhoekige limietbenadering van cirkels, maar ik heb er moeite mee te beweren dat het gemakkelijk of voor de hand liggend genoeg is om als “het juiste antwoord” te worden beschouwd.

Een van mijn Twitter-respondenten was bezorgd over hoe glad de kromme is. Deze grafsteen is continu differentieerbaar, maar niet tweemaal. Het zou zeker interessant zijn als veel mensen dachten dat dit een kritische kwestie was, en dit kan waarschijnlijk worden getest met een oneindig gladde grafsteen opgebouwd uit iets als dit, hoewel ik niet heb nagedacht over de details.

We zouden kunnen proberen dit als volgt te formaliseren: in een vierkant (of elke veelhoek) heeft een zijde de eigenschap dat je vanaf elke positie in het inwendige de vorm recht door je locatie kunt snijden, zodat je gekozen zijde stevig aan een kant van de snede ligt. Dat werkt niet voor de tweezijdige grafsteen: elke snede zal altijd de lange zijde doorsnijden. We zouden dit kunnen afzwakken door te zeggen dat om als zijde te tellen, er minstens één manier moet zijn om de vorm door te snijden zodat de zijde aan één kant van de snede ligt. Daardoor zouden we kunnen zeggen dat de grafsteen vier zijden heeft (ook al ligt het gebogen gedeelte niet aan één kant van de punten in het bovenste gebied). Voor de cirkel echter, is de veronderstelde ene zijde nooit aan één zijde (dus zou worden uitgesloten), en alleen het rechte gedeelte van een halve cirkel zou tellen als een zijde.

Het is niet eenvoudig om met een rigoureuze rechtvaardiging te komen die voor beide grafstenen werkt, maar ik denk meer informeel in termen van Schellingpunten: dat wil zeggen locaties die opvallen als bijzonder om redenen die misschien niet gemakkelijk van tevoren te voorspellen zijn.

Aankenningen

Dank aan iedereen die heeft meegedaan aan mijn polls of ze heeft geretweet, of die hierover met me heeft gediscussieerd op Twitter.