Wanneer we het over modelvoorspelling hebben, is het belangrijk om voorspellingsfouten (bias en variantie) te begrijpen. Er is een wisselwerking tussen het vermogen van een model om de bias en de variantie te minimaliseren. Een goed begrip van deze fouten zou ons niet alleen helpen om nauwkeurige modellen te bouwen, maar ook om de fout van overfitting en underfitting te vermijden.
Dus laten we beginnen met de basisprincipes en zien hoe ze verschil maken voor onze machine learning-modellen.
Wat is bias?
Bias is het verschil tussen de gemiddelde voorspelling van ons model en de juiste waarde die we proberen te voorspellen. Een model met een hoge bias besteedt zeer weinig aandacht aan de trainingsgegevens en oversimplificeert het model. Het leidt altijd tot een hoge fout op de trainings- en testgegevens.
Wat is variantie?
Variantie is de variabiliteit van de modelvoorspelling voor een gegeven gegeven datapunt of een waarde die ons de spreiding van onze gegevens vertelt. Een model met een hoge variantie besteedt veel aandacht aan de trainingsgegevens en generaliseert niet op de gegevens die het nog niet eerder heeft gezien. Dergelijke modellen presteren dus zeer goed op de trainingsgegevens, maar hebben hoge foutenpercentages op de testgegevens.
Mathematisch
Laat de variabele die we proberen te voorspellen staan als Y en andere covariaten als X. We nemen aan dat er tussen die twee een verband bestaat dat
Y=f(X) + e
Waarbij e de foutterm is en die normaal verdeeld is met een gemiddelde van 0.
We maken een model f^(X) van f(X) met behulp van lineaire regressie of een andere modelleringstechniek.
Dus de verwachte kwadratische fout in een punt x is
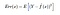
De Err(x) kan verder worden ontleed als

Err(x) is de som van Bias², variantie en de onherleidbare fout.
Onherleidbare fout is de fout die niet kan worden verminderd door goede modellen te maken. Het is een maat voor de hoeveelheid ruis in onze gegevens. Hier is het belangrijk te begrijpen dat hoe goed we ons model ook maken, onze gegevens een bepaalde hoeveelheid ruis of onherleidbare fout zullen bevatten die niet kan worden verwijderd.
Bias en variantie met behulp van het bulls-eye diagram

In het bovenstaande diagram is het centrum van het doel een model dat perfect correcte waarden voorspelt. Naarmate we ons verder van de roos verwijderen, worden onze voorspellingen slechter en slechter. We kunnen ons proces van modelbouw herhalen om afzonderlijke treffers op het doel te krijgen.
In supervised learning is er sprake van underfitting wanneer een model niet in staat is het onderliggende patroon van de gegevens te vatten. Deze modellen hebben meestal een hoge bias en een lage variantie. Het gebeurt wanneer we over heel weinig gegevens beschikken om een accuraat model te bouwen of wanneer we proberen een lineair model te bouwen met niet-lineaire gegevens. Ook zijn dit soort modellen zeer eenvoudig om de complexe patronen in de gegevens te vatten, zoals lineaire en logistische regressie.
In gesuperviseerd leren treedt overfitting op wanneer ons model de ruis samen met het onderliggende patroon in de gegevens vastlegt. Dit gebeurt wanneer we ons model veelvuldig trainen op een dataset met veel ruis. Deze modellen hebben een lage bias en een hoge variantie. Deze modellen zijn zeer complex, zoals beslisbomen, die gevoelig zijn voor overfitting.

Waarom is er sprake van Bias Variance Tradeoff?
Als ons model te eenvoudig is en zeer weinig parameters heeft, kan het een hoge bias en lage variantie hebben. Aan de andere kant, als ons model een groot aantal parameters heeft, zal het een hoge variantie en een lage bias hebben. We moeten dus het juiste/goede evenwicht zien te vinden zonder de gegevens te overfitten of te underfitten.
Door deze afweging van complexiteit is er een afweging tussen bias en variantie. Een algoritme kan niet tegelijkertijd complexer en minder complex zijn.
Totale fout
Om een goed model te bouwen, moeten we een goed evenwicht vinden tussen bias en variantie, zodat de totale fout wordt geminimaliseerd.


Een optimaal evenwicht tussen bias en variantie zou het model nooit over- of onder-fitten.
Inzicht in bias en variantie is dus van cruciaal belang om het gedrag van voorspellingsmodellen te begrijpen.
Bedankt voor het lezen.