GeeksforGeeks

Voorwaarde – Graph Theory Basics – Set 1
Een grafiek is een structuur die bestaat uit een verzameling objecten waarin sommige paren van de objecten in zekere zin “verwant” zijn. De objecten van de grafiek komen overeen met hoekpunten en de relaties tussen hen komen overeen met ribben. Een grafiek wordt schematisch weergegeven als een verzameling punten die hoekpunten voorstellen, verbonden door lijnen of krommen die randen voorstellen.
Vormelijk

“Een grafiek bestaat uit , een niet-lege verzameling hoekpunten (of knopen) en , een verzameling randen. Aan elke zijde zijn een of twee hoekpunten verbonden, die de eindpunten worden genoemd.”

Typen grafieken:Er zijn verschillende typen grafieken, onderscheiden op basis van het aantal randen, hun richting, hun gewicht enz.

1. Eenvoudige grafiek – Een grafiek waarin elke rand twee verschillende hoekpunten met elkaar verbindt en waarin geen twee randen hetzelfde hoekpuntenpaar met elkaar verbinden, wordt een eenvoudige grafiek genoemd. Neem bijvoorbeeld de volgende grafiek –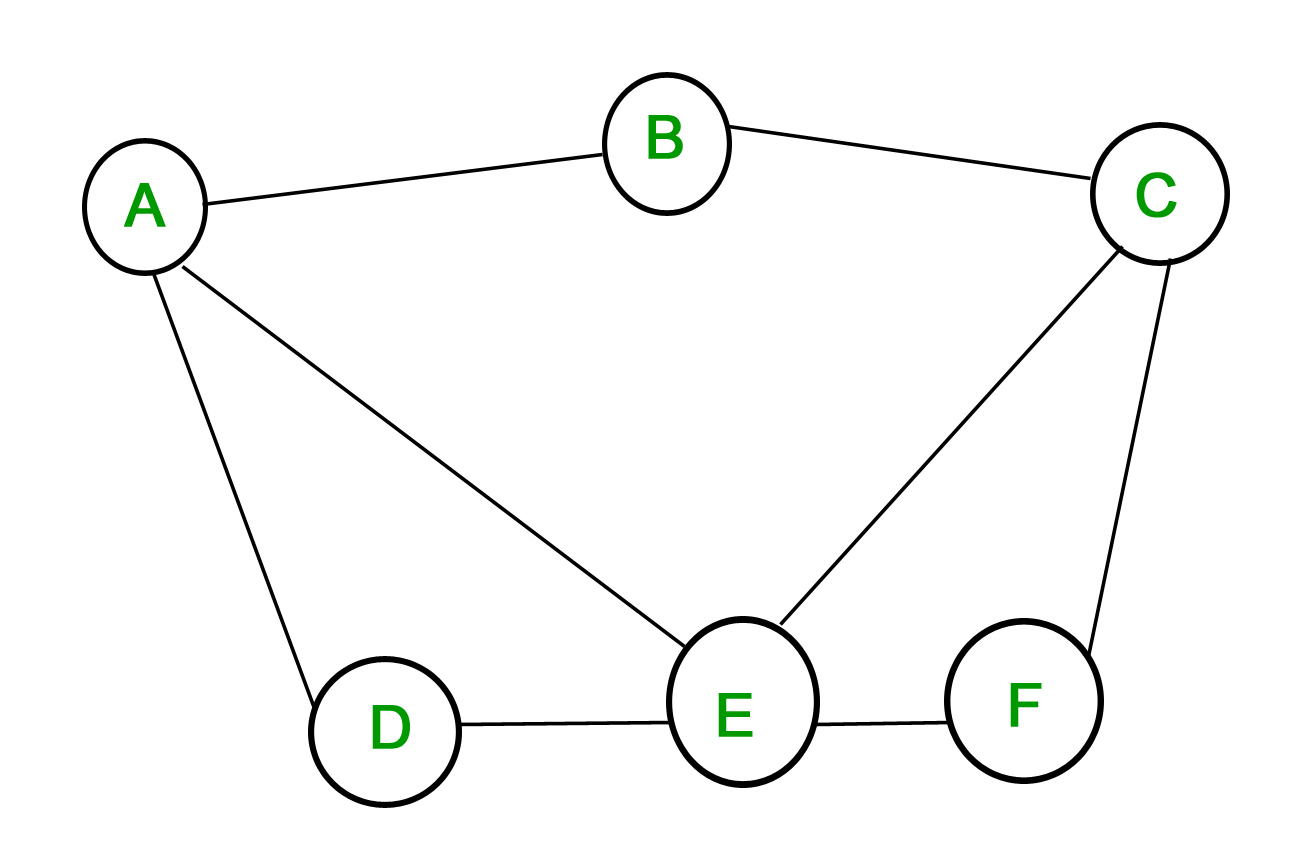

De bovenstaande grafiek is een eenvoudige grafiek, omdat geen enkel hoekpunt een eigen lus heeft en geen twee hoekpunten meer dan één rand hebben die hen verbindt.
De randen worden aangeduid met de hoekpunten die zij verbinden- is de rand die de hoekpunten en verbindt.

2. Multigrafiek – Een grafiek waarin meerdere ribben hetzelfde paar hoekpunten kunnen verbinden, wordt een multigrafiek genoemd.
Omdat er meerdere ribben tussen hetzelfde paar hoekpunten kunnen zijn, geeft de multipliciteit van de rand het aantal ribben tussen twee hoekpunten aan.

De bovenstaande grafiek is een multigrafiek omdat er meerdere ribben zijn tussen en . De multipliciteit van de rand is 2.

In sommige grafieken, in tegenstelling tot de hierboven getoonde, zijn de randen gericht. Dit betekent dat de relatie tussen de objecten slechts eenrichtingsverkeer is en niet tweerichtingsverkeer. De richting van de randen kan in sommige toepassingen van belang zijn.

Op basis van de vraag of de randen al dan niet gericht zijn, kunnen we gerichte grafieken en ongerichte grafieken hebben. Deze eigenschap kan worden uitgebreid tot eenvoudige grafieken en multigrafieken om eenvoudige gerichte of ongerichte eenvoudige grafieken en gerichte of ongerichte multigrafieken te krijgen.

Basisterminologie voor grafieken :

In de bovenstaande bespreking zijn reeds enkele termen met betrekking tot grafieken uitgelegd, zoals hoekpunten, ribben, gerichte en ongerichte ribben enz. Er zijn meer termen die eigenschappen van hoekpunten en ribben beschrijven.

• Adjacency – In een grafiek zegt men dat twee hoekpunten en aangrenzend zijn als zij de eindpunten van een ribbe zijn. Men zegt dat de rand met de hoekpunten incident is.
  In het geval dat de rand gericht is, zegt men dat aan grenst en dat aan grenst. Hier wordt het beginpunt en het eindpunt genoemd.
• Graad – De graad van een hoekpunt is het aantal ribben dat ermee samenvalt, behalve de zelflus, die tweemaal bijdraagt tot de graad van het hoekpunt. De graad van een vertex wordt aangeduid als .
  In het geval van gerichte grafieken wordt de graad verder geclassificeerd in in-graad en uit-graad. De in-graad van een vertex is het aantal ribben met het gegeven vertex als eindvertex. De out-graad van een vertex is het aantal edges met het gegeven vertex als beginvertex. De in-graad wordt aangeduid als en de uit-graad als .
  In de hierboven getoonde gerichte grafiek van vluchten tussen steden is de in-graad van het hoekpunt “Delhi” bijvoorbeeld 3 en zijn uit-graad eveneens 3.

Noot: Als een hoekpunt een graad nul heeft, wordt het geïsoleerd genoemd. Als de graad één is, heet het pendant.

Handshaking Theorem :

Wat zou men krijgen als men de graden van alle hoekpunten van een grafiek optelt. In het geval van een ongerichte grafiek draagt elke rand twee keer bij, eenmaal voor zijn beginpunt en de tweede keer voor zijn eindpunt. De som van de graden is dus gelijk aan tweemaal het aantal ribben. Dit feit staat in de Handshaking Theorem.

Let  be an undirected graph with  edges. ThenIn case G is a directed graph,

De handshaking theorem, voor ongerichte grafieken, heeft een interessant resultaat –

An undirected graph has an even number of vertices of odd degree.

Proof : Stel en zijn de verzamelingen van hoekpunten van respectievelijk even en oneven graden.
We weten door de handshaking theorem dat,

Dus,

De som van graden van hoekpunten met even graden is even. De LHS is ook even, wat betekent dat de som van de graden van hoekpunten met oneven graden even moet zijn.
Dus, het aantal hoekpunten met oneven graden is even.

Enkele speciale Eenvoudige Grafieken :

1. Volledige grafieken – Een eenvoudige grafiek van hoekpunten met precies één rand tussen elk hoekpuntenpaar wordt een volledige grafiek genoemd. Een volledige grafiek van hoekpunten wordt aangeduid met . Het totaal aantal ribben is n*(n-1)/2 met n hoekpunten in een volledige grafiek.

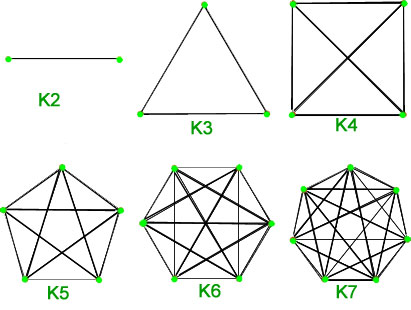
2. Cycli – Cycli zijn eenvoudige grafieken met hoekpunten en ribben . Cyclus met hoekpunten wordt aangeduid als . Totaal aantal ribben is n met n hoekpunten in cyclusgrafiek.

3. Wielen – Een wiel is net als een cyclus, met één extra hoekpunt dat met elk ander hoekpunt verbonden is. Wielen van hoekpunten met 1 extra hoekpunt worden aangeduid met . Het totale aantal ribben is 2*(n-1) met n hoekpunten in een wielgrafiek.

4. Hyperkubus – De hyperkubus of n-kubus is een grafiek met hoekpunten die elk worden voorgesteld door een n-bits tekenreeks. De hoekpunten die ten hoogste 1 bit van elkaar verschillen, zijn verbonden door ribben. Een hyperkubus van hoekpunten wordt aangeduid met . Het totale aantal ribben is n* met hoekpunten in de kubusgrafiek.

5. Bipartiete grafieken – Van een eenvoudige grafiek wordt gezegd dat hij bipartiet is als de verzameling hoekpunten in twee disjuncte verzamelingen kan worden verdeeld, zodat elke rand in zijn beginkruispunt in de eerste verzameling heeft en het eindpunt in de tweede verzameling. Het totaal aantal ribben is (n*m) met (n+m) hoekpunten in een bipartiete grafiek.

Stelling – Een eenvoudige grafiek is bipartiet als en slechts als het mogelijk is om aan elk hoekpunt van de grafiek een van twee
verschillende kleuren toe te kennen, zodat geen twee aangrenzende dezelfde kleur krijgen toegewezen.

Een tweeledige grafiek met en hoekpunten in zijn twee disjuncte deelverzamelingen heet compleet te zijn als er een rand is van elk hoekpunt in de eerste verzameling naar elk hoekpunt in de tweede verzameling, voor een totaal van randen. Een volledige bipartiete grafiek met hoekpunten in de eerste verzameling en hoekpunten in de tweede verzameling wordt aangeduid als .

GATE CS Hoekvragen

Het oefenen van de volgende vragen zal je helpen je kennis te testen. Alle vragen zijn gesteld in GATE in voorgaande jaren of in GATE Mock Tests. Het wordt ten zeerste aanbevolen dat je ze oefent.

1. GATE CS 2013, vraag 25
2. GATE CS 2014 Set-1, vraag 61
3. GATE CS 2006, vraag 71
4. GATE CS 2002, vraag 25
5. GATE CS 2004, vraag 37
6. GATE CS 2014 Set-2, vraag 13

Referenties-

Graphs – Wikipedia
Discrete Mathematics and its Applications, door Kenneth H Rosen

Dit artikel is bijgedragen door Chirag Manwani. Als je GeeksforGeeks leuk vindt en een bijdrage wilt leveren, kun je ook een artikel schrijven via contribute.geeksforgeeks.org of mail je artikel naar [email protected]. Zie je artikel verschijnen op de GeeksforGeeks hoofdpagina en help andere Geeks.