- Connectiviteit is een basisbegrip van de grafentheorie. Het definieert of een grafiek verbonden of verbroken is. Zonder connectiviteit is het niet mogelijk een grafiek van een hoekpunt naar een ander hoekpunt te doorkruisen.
- Een grafiek wordt verbonden genoemd als er een pad is tussen elk paar hoekpunten. Van elk hoekpunt naar elk ander hoekpunt moet er een pad zijn om te doorkruisen. Dit wordt de connectiviteit van een grafiek genoemd.
- Een grafiek wordt losgekoppeld genoemd, als er meerdere losgekoppelde hoekpunten en randen bestaan.
- Grafiekconnectiviteitstheorieën zijn essentieel in netwerktoepassingen, routering van transportnetwerken, netwerktolerantie enz.
Voorbeeld
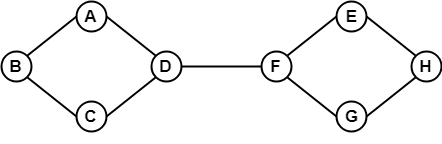
In het bovenstaande voorbeeld is het mogelijk om van een hoekpunt naar een ander hoekpunt te reizen. Hier kunnen we van hoekpunt B naar H reizen via het pad B -> A -> D -> F -> E -> H. Het is dus een verbonden grafiek.
Voorbeeld
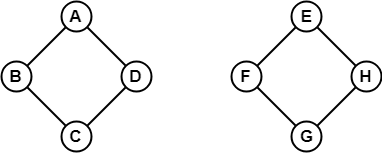
In bovenstaand voorbeeld is het niet mogelijk om van hoekpunt B naar H te reizen omdat er geen pad direct of indirect tussen beide bestaat. Het is dus een ontkoppelde grafiek.
Laten we enkele basisbegrippen van connectiviteit bekijken.
Cut Vertex
Een enkelvoudig vertex waarvan de verwijdering een grafiek ontkoppelt, wordt een cut-vertex genoemd.
Laat G een ontkoppelde grafiek zijn. Een hoekpunt v van G heet een afgesneden hoekpunt van G, als G-v (Verwijder v uit G) een ontkoppelde grafiek oplevert.
Wanneer we een hoekpunt uit een grafiek verwijderen, dan zal de grafiek in twee of meer grafieken uiteenvallen. Dit hoekpunt wordt een geknipt hoekpunt genoemd.
Noot: Stel G is een grafiek met n hoekpunten:
- Een verbonden grafiek G kan maximaal (n-2) geknipte hoekpunten hebben.
- Het verwijderen van een geknipt hoekpunt kan een ontkoppelde grafiek tot gevolg hebben.
- Het verwijderen van een hoekpunt kan het aantal componenten in een grafiek met ten minste één doen toenemen.
- Elk niet-hangend hoekpunt van een boom is een afgesneden hoekpunt.
Voorbeeld 1

Voorbeeld 2
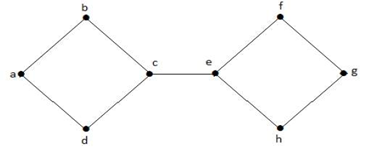
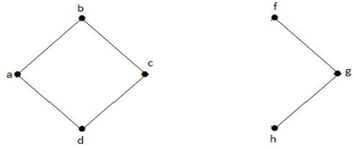
In de bovenstaande grafiek is hoekpunt ‘e’ een afgesneden hoekpunt. Nadat vertex ‘e’ uit bovenstaande grafiek is verwijderd, wordt de grafiek een ontkoppelde grafiek.
Cut Edge (Bridge)
Een cut- edge of bridge is een enkele edge waarvan de ontkoppeling van een grafiek wordt opgeheven.
Laat G een verbonden grafiek zijn. Een rand e van G heet een afgesneden rand van G, indien G-e (verwijder e uit G) een ontkoppelde grafiek oplevert.
Wanneer we een rand uit een grafiek verwijderen, zal de grafiek in twee of meer grafieken uiteenvallen. Deze verwijderde rand heet een snijrand of bridge.
Note: Zij G een grafiek met n hoekpunten:
- Een verbonden grafiek G kan ten hoogste (n-1) snijranden hebben.
- Het verwijderen van een snijrand kan een ontkoppelde grafiek tot gevolg hebben.
- Herhaling van een snijrand kan het aantal componenten in een grafiek met ten hoogste één doen toenemen.
- Een snijrand ‘e’ mag geen deel zijn van een cyclus in G.
- Als er een snijrand bestaat, moet er ook een snijvertex bestaan, want ten minste één vertex van een snijrand is een snijvertex.
- Als een afgesneden hoekpunt bestaat, dan is het bestaan van een willekeurige afgesneden rand niet noodzakelijk.
Voorbeeld 1
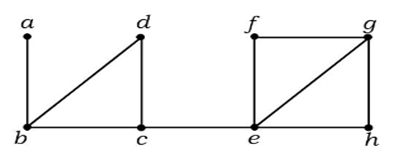
In bovenstaande grafiek is rand (c, e) een afgesneden rand. Na het verwijderen van deze rand uit bovenstaande grafiek zal de grafiek een ontkoppelde grafiek worden.
Voorbeeld 2
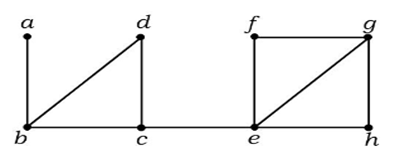
In bovenstaande grafiek is rand (c, e) een ingesneden rand. Na verwijdering van deze rand uit bovenstaande grafiek wordt de grafiek een ontkoppelde grafiek.
Cut Set
In een verbonden grafiek G is een cut set een verzameling S van randen met de volgende eigenschappen:
- Het verwijderen van alle randen in S ontkoppelt G.
- Het verwijderen van sommige (maar niet alle) ribben in S leidt niet tot ontkoppeling van G.
Voorbeeld 1
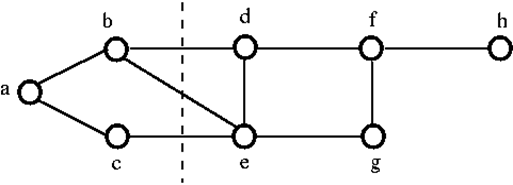
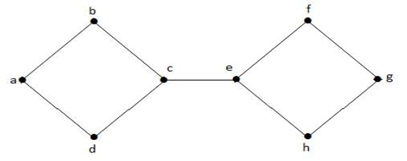
Om de bovenstaande grafiek G te ontkoppelen, moeten we de drie ribben verwijderen, te weten bd, be en ce. We kunnen de grafiek niet ontkoppelen door slechts twee van de drie randen te verwijderen. Daarom is {bd, be, ce} een verzameling van sneden.
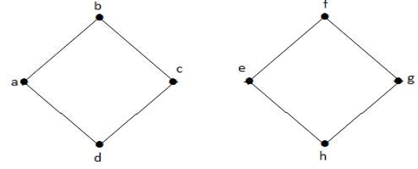
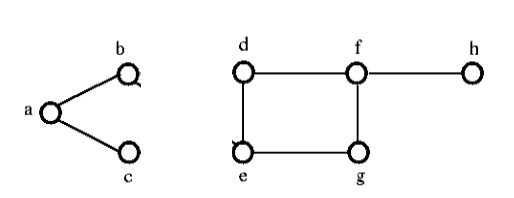
Na verwijdering van de verzameling van sneden uit de bovenstaande grafiek, ziet deze er als volgt uit:
Endge Connectivity
De edge connectivity van een verbonden grafiek G is het minimum aantal sneden waarvan de verwijdering G ontkoppeld maakt. Het wordt aangeduid met λ(G).
Wanneer λ(G) ≥ k, dan wordt de grafiek G k-rand-connectief genoemd.
Voorbeeld
Laten we eens een voorbeeld bekijken,
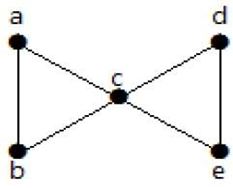
Van de bovenstaande grafiek wordt de verbonden grafiek, door twee minimale randen te verwijderen, een ontkoppelde grafiek. De randconnectiviteit is dus 2. De bovenstaande grafiek is dus een 2-edge-connected graph.
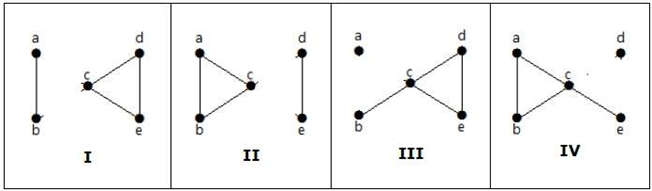
Hier volgen vier manieren om de grafiek te ontkoppelen door twee randen te verwijderen:
Vertexconnectiviteit
De connectiviteit (of vertexconnectiviteit) van een verbonden grafiek G is het minimumaantal hoekpunten waarvan verwijdering G ontkoppelt of reduceert tot een triviale grafiek. Zij wordt aangeduid met K(G).
De grafiek wordt k-verbonden of k-tex verbonden genoemd als K(G) ≥ k. Om een vertex te verwijderen, moeten ook de bijbehorende ribben worden verwijderd.
Voorbeeld
Laten we eens een voorbeeld bekijken:
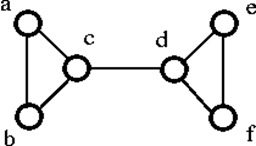
De bovenstaande grafiek G kan worden ontkoppeld door één enkel hoekpunt “c” of “d” te verwijderen. De vertexconnectiviteit is dus 1. Het is dus een grafiek met 1 connectiviteit.