Chemische kinetiek
Chemische kinetiek
Je bent misschien bekend met zuur-base titraties waarbij fenolftaleïne als eindpuntindicator wordt gebruikt. Het is u misschien echter niet opgevallen wat er gebeurt wanneer een oplossing die fenolftaleïne bevat in aanwezigheid van een overmaat base een paar minuten mag staan. Hoewel de oplossing aanvankelijk een roze kleur heeft, wordt zij geleidelijk kleurloos naarmate de fenolftaleïne reageert met het OH-ion in een sterk basische oplossing.
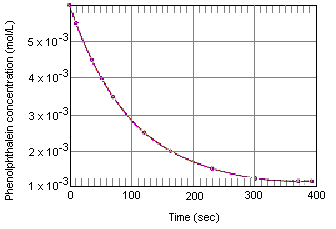
De onderstaande tabel laat zien wat er gebeurt met de concentratie van fenolftaleïne in een oplossing die aanvankelijk 0,005 M fenolftaleïne en 0,61 M OH-ion bevatte. Zoals u kunt zien wanneer deze gegevens in de onderstaande grafiek worden uitgezet, daalt de fenolftaleïneconcentratie met een factor 10 over een periode van ongeveer vier minuten.
Experimentele gegevens voor de reactie tussen fenolftaleïne en overmaat base
Experimenten zoals degene die ons de gegevens in bovenstaande tabel heeft opgeleverd, worden geclassificeerd als metingen van de chemische kinetiek (van een Griekse stam die “bewegen” betekent). Een van de doelen van deze experimenten is de reactiesnelheid te beschrijven – de snelheid waarmee de reactanten worden omgezet in de producten van de reactie.
De term snelheid wordt vaak gebruikt om de verandering in een grootheid te beschrijven die per tijdseenheid optreedt. Het inflatiepercentage is bijvoorbeeld de verandering van de gemiddelde kosten van een verzameling standaardartikelen per jaar. De snelheid waarmee een voorwerp door de ruimte reist is de afstand die per tijdseenheid wordt afgelegd, zoals mijl per uur of kilometer per seconde. In de chemische kinetiek is de afgelegde afstand de verandering in de concentratie van een van de componenten van de reactie. De snelheid van een reactie is dus de verandering in de concentratie van een van de reactanten![]() (X)
(X)![]() die optreedt in een gegeven tijdsperiode
die optreedt in een gegeven tijdsperiode![]() t.
t.
![]()
Oefening Opgave 1:
Gebruik de gegevens in bovenstaande tabel om de snelheid te berekenen waarmee fenolftaleïne reageert met het OH-ion gedurende elk van de volgende perioden:
(a) Gedurende het eerste tijdsinterval, wanneer de concentratie fenolftaleïne daalt van 0,0050 M tot 0,0045 M.
(b) In het tweede tijdsinterval, wanneer de concentratie daalt van 0,0045 M tot 0,0040 M.
(c) In het derde tijdsinterval, wanneer de concentratie daalt van 0,0040 M tot 0,0035 M.
Klik hier om uw antwoord op Oefenopgave 1 te controleren.
Klik hier om een oplossing te zien van Oefenprobleem 1.
![]()
Instantiële reactiesnelheden en de snelheidswet voor een reactie
De snelheid van de reactie tussen fenolftaleïne en het OH-ion is niet constant; deze verandert met de tijd. Zoals de meeste reacties neemt de snelheid van deze reactie geleidelijk af naarmate de reactanten worden verbruikt. Dit betekent dat de reactiesnelheid verandert terwijl deze wordt gemeten.
Om de fout die hierdoor in onze metingen ontstaat zo klein mogelijk te houden, lijkt het raadzaam de reactiesnelheid te meten over perioden die kort zijn in vergelijking met de tijd die de reactie nodig heeft om op te treden. We kunnen bijvoorbeeld proberen de oneindig kleine verandering in concentratie![]() d(X)
d(X)![]() te meten die optreedt in een oneindig korte tijdsperiodeedt. De verhouding tussen deze hoeveelheden wordt de momentane reactiesnelheid genoemd.
te meten die optreedt in een oneindig korte tijdsperiodeedt. De verhouding tussen deze hoeveelheden wordt de momentane reactiesnelheid genoemd.
![]()
De momentane reactiesnelheid op elk moment kan worden berekend uit een grafiek van de concentratie van de reactant (of het product) tegen de tijd. Onderstaande grafiek laat zien hoe de reactiesnelheid voor de ontleding van fenolftaleïne kan worden berekend uit een grafiek van de concentratie tegen de tijd. De reactiesnelheid op een bepaald moment in de tijd is gelijk aan de helling van een raaklijn aan deze kromme op dat moment.
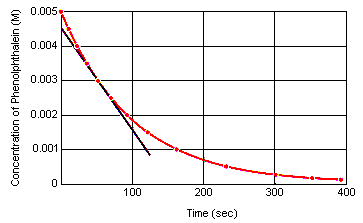
De momentane reactiesnelheid kan worden gemeten op elk moment tussen het moment waarop de reagentia worden gemengd en het moment waarop de reactie evenwicht bereikt.Extrapolatie van deze gegevens terug naar het moment waarop de reagentia worden gemengd, levert de momentane beginsnelheid van de reactie op.
![]()
Snelheidswetten en snelheidsconstanten
Een interessant resultaat wordt verkregen wanneer de momentane reactiesnelheid wordt berekend op verschillende punten langs de kromme in de grafiek uit het vorige hoofdstuk. De reactiesnelheid op elk punt van deze curve is recht evenredig met de concentratie fenolftaleïne op dat moment.
Rate = k(fenolftaleïne)
Omdat deze vergelijking een experimentele wet is die de reactiesnelheid beschrijft, wordt zij de snelheidswet van de reactie genoemd. De evenredigheidsconstante, k, wordt de snelheidsconstante genoemd.
Praktijkopgave 2:
Bereken de snelheidsconstante voor de reactie tussen fenolftaleïne en het OH-ion als de momentane reactiesnelheid 2,5 x 10-5 mol per liter per seconde is bij een concentratie van fenolftaleïne van 0,0025 M.
Klik hier om uw antwoord op Praktijkopgave 2 te controleren.
Klik hier om de oplossing van Praktijkopgave 2 te zien.
Praktijkopgave 3:
Gebruik de snelheidsconstante voor de reactie tussen fenolftaleïne en het OH-ion om de initiële momentane reactiesnelheid te berekenen voor de experimentele gegevens die in de voorgaande tabel staan.
Klik hier om uw antwoord op practicumopgave 3 te controleren.
Klik hier om de oplossing van practicumopgave 3 te bekijken.
![]()
Verschillende manieren om de reactiesnelheid uit te drukken
Er is meestal meer dan één manier om de snelheid van een reactie te meten. We kunnen bijvoorbeeld de ontleding van waterstofjodide bestuderen door de snelheid te meten waarmee ofwel H2 ofwel I2 wordt gevormd in de volgende reactie of de snelheid waarmee HI wordt verbruikt.
2 HI(g) H2(g) + I2(g)
Uit experimenten blijkt dat de snelheid waarmee I2 wordt gevormd evenredig is met het kwadraat van de HI-concentratie op elk moment in de tijd.
![]()
Wat zou er gebeuren als we de snelheid bestudeerden waarmee H2 wordt gevormd? De evenwichtsvergelijking suggereert dat H2 en I2 met precies dezelfde snelheid moeten worden gevormd.
![]()
Wat zou er echter gebeuren als we de snelheid bestudeerden waarmee HI in deze reactie wordt verbruikt? Omdat HI wordt verbruikt, moet de verandering in de concentratie een negatief getal zijn. Volgens afspraak wordt de snelheid van een reactie altijd als positief getal gerapporteerd. Daarom moeten we het teken veranderen voordat we de reactiesnelheid vermelden van een stof die bij de reactie wordt verbruikt.
![]()
Het negatieve teken doet twee dingen. Wiskundig zet het een negatieve verandering in de concentratie van HI om in een positieve snelheid. Fysisch herinnert het ons eraan dat de concentratie van de reactant afneemt met de tijd.
Wat is het verband tussen de reactiesnelheid die wordt verkregen door de vorming van H2 of I2 te volgen en de snelheid die wordt verkregen door HI te zien verdwijnen? Volgens de stoichiometrie van de reactie worden voor elke geproduceerde molecule H2 of I2 twee HI-moleculen verbruikt. Dit betekent dat de afbraaksnelheid van HI twee keer zo snel is als de snelheid waarmee H2 en I2 worden gevormd. We kunnen deze relatie als volgt in een wiskundige vergelijking omzetten.
![]()
Dientengevolge is de snelheidsconstante die men verkrijgt door de snelheid te bestuderen waarmee H2 en I2 worden gevormd in deze reactie (k) niet dezelfde als de snelheidsconstante die men verkrijgt door de snelheid te bestuderen waarmee HI wordt verbruikt (k’)
Oefening Opgave 4:
Bereken de snelheid waarmee HI verdwijnt in de volgende reactie op het moment dat I2 wordt gevormd met een snelheid van 1.8 x 10-6 mol per liter per seconde:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Klik hier om uw antwoord op Oefenprobleem 4 te controleren.
Klik hier om een oplossing van Oefenprobleem 4 te zien.
![]()
De snelheidswet versus de stoichiometrie van een reactie
In de jaren dertig bestudeerden Sir Christopher Ingold en zijn collega’s aan de universiteit van Londen de kinetiek van substitutiereacties zoals de volgende.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Zij stelden vast dat de snelheid van deze reactie evenredig is met deconcentraties van beide reactanten.
Snelheid = k(CH3Br)(OH-)
Toen ze een soortgelijke reactie uitvoerden met een iets ander uitgangsmateriaal, kregen ze vergelijkbare producten.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Maar nu was de reactiesnelheid evenredig met de concentratie van slechts één van de reactanten.
Rate = k((CH3)3CBr)
Deze resultaten illustreren een belangrijk punt: De snelheidswet voor een reactie kan niet worden voorspeld uit de stoichiometrie van de reactie; deze moet proefondervindelijk worden vastgesteld. Soms is de snelheidswet consistent met wat we verwachten uit de stoichiometrie van de reactie.
2 HI(g) H2(g) + I2(g)
Rate = k(HI)2
Vaak is dat niet zo, is dat echter niet het geval.
| 2 N2O5(g) |
Snelheid = k(N2O5) |
![]()
Orde van moleculariteit
Sommige reacties verlopen in één enkele stap. De reactie waarbij een chlooratoom wordt overgedragen van ClNO2 naar NO om NO2 en ClNO te vormen, is een goed voorbeeld van een eenstapsreactie.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Andere reacties verlopen via een reeks afzonderlijke stappen. N2O5, bijvoorbeeld, ontleedt in NO2 en O2 door een drie-stappen-mechanisme.
| Stap 1: | N2O5 |
|
| Stap 2: | NO2 + NO3 |
|
| Stap 3: | NO + NO3 |
De stappen in een reactie worden ingedeeld in termen van moleculariteit, waarmee het aantal verbruikte moleculen wordt aangeduid. Wanneer één enkel molecuul wordt verbruikt, wordt de stap unimoleculair genoemd. Wanneer twee moleculen worden verbruikt, is de stap bimoleculair.
Oefening 5:
Bepaal de moleculariteit van elke stap in de reactie waarbij N2O5 ontleedt tot NO2 en O2.
Klik hier om uw antwoord op Oefening 5 te controleren.
Klik hier om een oplossing te zien voor Oefening 5.
Reacties kunnen ook worden ingedeeld in volgorde. De ontleding van N2O5 is een eerste-orde reactie omdat de reactiesnelheid afhangt van de concentratie van N2O5 tot de eerste macht verheven.
Snelheid = k(N2O5)
De ontleding van HI is een tweede-orde reactie omdat de reactiesnelheid afhangt van de concentratie van HI tot de tweede macht verheven.
Snelheid = k(HI)2
Wanneer de snelheid van een reactie van meer dan één reagens afhangt, delen we de reactie in naar de volgorde van elk reagens.
Praktijkopgave 6:
Klasseer de volgorde van de reactie tussen NO en O2 tot NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Aanname van de volgende snelheidswet voor deze reactie:
Snelheid = k(NO)2(O2)
Klik hier om uw antwoord op Praktijkopgave 6 te controleren.
Het verschil tussen de moleculariteit en de volgorde van een reactie is belangrijk. De moleculariteit van een reactie, of een stap binnen een reactie, beschrijft wat er op moleculair niveau gebeurt. De volgorde van een reactie beschrijft wat er op macroscopische schaal gebeurt. We bepalen de volgorde van een reactie door te kijken hoe de producten van een reactie verschijnen of de reactanten verdwijnen. De moleculariteit van de reactie is iets wat we afleiden om deze experimentele resultaten te verklaren.
![]()
Botsingstheorie model van chemische reacties
Het botsingstheorie model van chemische reacties kan worden gebruikt om de waargenomen snelheidswetten voor zowel eenstaps- als meerstapsreacties te verklaren. Dit model gaat ervan uit dat de snelheid van elke stap in een reactie afhangt van de frequentie van de botsingen tussen de bij die stap betrokken deeltjes.
De onderstaande figuur biedt een basis voor het begrijpen van de implicaties van het botsingstheoretische model voor eenvoudige, eenstapsreacties, zoals de volgende.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
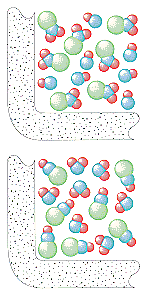
De kinetische moleculaire theorie gaat ervan uit dat het aantal botsingen per seconde in een gas afhangt van het aantal deeltjes per liter. De snelheid waarmee NO2en ClNO bij deze reactie worden gevormd, zou dus recht evenredig moeten zijn met de concentraties van zowel ClNO2 als NO.
Rate = k(ClNO2)(NO)
Het botsingstheoretische model suggereert dat de snelheid van elke stap in een reactie evenredig is met de concentraties van de reagentia die bij die stap worden verbruikt. De snelheidswet voor een eenstapsreactie moet daarom overeenkomen met de stoichiometrie van die reactie.
De volgende reactie, bijvoorbeeld, verloopt in één stap.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Wanneer deze moleculen in de juiste oriëntatie op elkaar botsen, kan een paar niet-bindende elektronen op het OH-ion worden afgestaan aan het koolstofatoom in het centrum van het CH3Br-molecuul, zoals te zien is in de figuur hieronder.
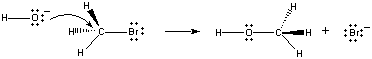
Wanneer dit gebeurt, vormt zich een koolstof-zuurstofverbinding op hetzelfde moment dat de koolstof-broomverbinding wordt verbroken. Het nettoresultaat van deze reactie is de vervanging van een Br-ion door een OH-ion. Omdat de reactie in één stap verloopt, waarbij botsingen tussen de twee reactanten optreden, is de snelheid van deze reactie evenredig met de concentratie van beide reactanten.
Snelheid = k(CH3Br)(OH-)
Niet alle reacties verlopen in één stap. De volgende reactie verloopt in drie stappen, zoals uit de onderstaande figuur blijkt.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
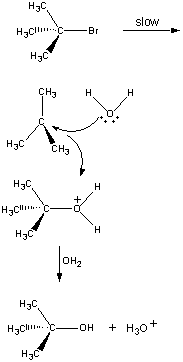
In de eerste stap splitst de (CH3)3CBr-molecule zich in een ionenpaar.
| Eerste stap | 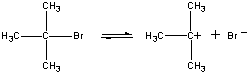 |
Het positief geladen (CH3)3C+-ion reageert vervolgens met water in een tweede stap.
| Tweede stap | 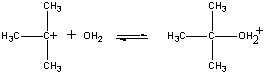 |
Het product van deze reactie verliest vervolgens in de laatste stap een proton aan ofwel het OH-ion ofwel aan water.
| Derde stap | 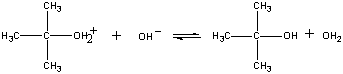 |
De tweede en derde stap in deze reactie gaan zeer veel sneller dan de eerste.
| (CH3)3CBr |
Slow step | |
| (CH3)3C+ + H2O |
Fast step | |
| (CH3)3COH2+ + OH- |
Snelle stap |
De totale reactiesnelheid is dus min of meer gelijk aan de snelheid van de eerste stap. De eerste stap wordt daarom de snelheidsbeperkende stap in deze reactie genoemd, omdat hij letterlijk de snelheid beperkt waarmee de producten van de reactie kunnen worden gevormd. Omdat bij de snelheidsbeperkende stap slechts één reagens betrokken is, is de totale reactiesnelheid evenredig met de concentratie van alleen dit reagens.
Snelheid = k((CH3)3CBr)
De snelheidswet voor deze reactie wijkt dus af van wat we op grond van de stoichiometrie van de reactie zouden voorspellen. Hoewel bij de reactie zowel (CH3)3CBrand OH- wordt verbruikt, is de snelheid van de reactie alleen evenredig met de concentratie van (CH3)3CBr.
De snelheidswetten voor chemische reacties kunnen worden verklaard met de volgende algemene regels.
De snelheid van elke stap in een reactie is recht evenredig met de concentraties van de reagentia die bij die stap worden verbruikt.
De totale snelheidswet voor een reactie wordt bepaald door de opeenvolging van stappen, of het mechanisme, waarmee de reactanten worden omgezet in de producten van de reactie.
De totale snelheidswet voor een reactie wordt gedomineerd door de snelheidswet voor de langzaamste stap in de reactie.