Realizações de Aprendizagem

  • Determinar se os dados ou um cenário descrevem crescimento linear ou geométrico
  • Identificar taxas de crescimento, valores iniciais ou valores pontuais expressos verbalmente, graficamente, ou numericamente, e traduzi-las num formato utilizável no cálculo
  • Calcular equações recursivas e explícitas para o crescimento linear e geométrico com informação suficiente, e usar essas equações para fazer previsões

A manutenção de uma taxa de variação constante é a característica definidora do crescimento linear. Plotagem de pares de coordenadas associadas à mudança constante resultará em uma linha reta, a forma do crescimento linear. Nesta seção, vamos formalizar uma forma de descrever o crescimento linear usando termos e conceitos matemáticos. Ao final desta seção, você será capaz de escrever tanto uma equação recursiva quanto uma explícita para o crescimento linear, dadas as condições iniciais, ou uma constante de mudança. Você também será capaz de reconhecer a diferença entre crescimento linear e geométrico dado um gráfico ou uma equação.

Crescimento linear (algébrico)

Previsão de crescimento

Marco é um coletor de garrafas de refrigerantes antigos. A sua colecção contém actualmente 437 garrafas. Todos os anos, ele orçamenta dinheiro suficiente para comprar 32 garrafas novas. Podemos determinar quantas garrafas ele terá em 5 anos, e quanto tempo levará para sua coleção chegar a 1000 garrafas?

Embora você possa provavelmente resolver ambas as questões sem uma equação ou matemática formal, vamos formalizar nossa abordagem a este problema para fornecer um meio de responder perguntas mais complicadas.

Suponha que Pn representa o número, ou população, de garrafas que Marco tem após n anos. Então P0 representaria o número de garrafas agora, P1 representaria o número de garrafas após 1 ano, P2 representaria o número de garrafas após 2 anos, e assim por diante. Poderíamos descrever como a coleção de garrafas de Marco está mudando usando:

P0 = 437

Pn = Pn-1 + 32

Isto é chamado de relação recursiva. Uma relação recursiva é uma fórmula que relaciona o próximo valor em uma seqüência com os valores anteriores. Aqui, o número de garrafas no ano n pode ser encontrado adicionando 32 ao número de garrafas do ano anterior, Pn-1. Usando esta relação, podemos calcular:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Respondemos à pergunta de quantas garrafas o Marco terá em 5 anos.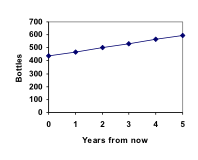

No entanto, resolver quanto tempo levará para que sua coleção chegue a 1000 garrafas exigiria muito mais cálculos.

Embora as relações recursivas sejam excelentes para descrever de forma simples e limpa como uma quantidade está mudando, elas não são convenientes para fazer previsões ou resolver problemas que se estendem muito para o futuro. Para isso, é preferível uma forma fechada ou explícita para o relacionamento. Uma equação explícita nos permite calcular Pn diretamente, sem necessidade de conhecer Pn-1. Embora você já seja capaz de adivinhar a equação explícita, vamos derivá-la a partir da fórmula recursiva. Podemos fazer isso não simplificando seletivamente como vamos:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Você provavelmente pode ver o padrão agora, e generalizar que

Pn = 437 + n(32) = 437 + 32n

Usando esta equação, podemos calcular quantas garrafas ele terá após 5 anos:

P5 = 437 + 32(5) = 437 + 160 = 597

Agora também podemos resolver para quando a recolha atingirá 1000 garrafas, substituindo em 1000 por Pn e resolvendo para n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Então Marco alcançará 1000 garrafas em 18 anos.

Os passos para determinar a fórmula e resolver o problema da coleção de garrafas de Marco são explicados em detalhes nos seguintes vídeos.

Neste exemplo, a coleção de Marco cresceu com o mesmo número de garrafas a cada ano. Esta mudança constante é a característica definidora do crescimento linear. Traçando os valores que calculamos para a coleção do Marco, podemos ver os valores formando uma linha reta, a forma de crescimento linear.

Crescimento linear

Se uma quantidade começa no tamanho P0 e cresce em d a cada período, então a quantidade após n períodos de tempo pode ser determinada usando qualquer uma dessas relações:

Forma recursiva

Pn = Pn-1 + d

Forma explícita

Pn = P0 + d n

Nesta equação, d representa a diferença comum – a quantidade que a população muda cada vez que n aumenta em 1.

Ligação à Aprendizagem Prévia: Inclinação e Intercepção

Pode reconhecer a diferença comum, d, na nossa equação linear como inclinação. Na verdade, toda a equação explícita deve parecer familiar – é a mesma equação linear que você aprendeu em álgebra, provavelmente declarada como y = mx + b.

Na equação algébrica padrão y = mx + b, b era o intercepção y, ou o valor y quando x era zero. Na forma da equação que estamos usando, estamos usando P0 para representar aquele valor inicial.

Na equação y = mx + b, lembre-se que m era a inclinação. Você pode se lembrar disso como “subir sobre a execução”, ou a mudança em y dividida pela mudança em x. De qualquer forma, representa a mesma coisa que a diferença comum, d, estamos usando – a quantidade que o output Pn muda quando a entrada n aumenta em 1,

As equações y = mx + b e Pn = P0 + d n significam a mesma coisa e podem ser usadas das mesmas maneiras. Estamos apenas escrevendo um pouco diferente.

Exemplos

A população de alce em uma floresta nacional foi medida para ser 12.000 em 2003, e foi medida novamente para ser 15.000 em 2007. Se a população continuar a crescer linearmente neste ritmo, qual será a população de alces em 2014?

Mostrar Solução

Para começar, precisamos definir como vamos medir n. Lembre-se que P0 é a população quando n = 0, então provavelmente não queremos usar literalmente o ano 0. Como já conhecemos a população em 2003, vamos definir n = 0 para ser o ano 2003.

Então P0 = 12.000.

Próximo precisamos encontrar d. Lembre-se que d é o crescimento por período de tempo, neste caso crescimento por ano. Entre as duas medidas, a população cresceu 15.000-12.000 = 3.000, mas demorou 2007-2003 = 4 anos para crescer tanto. Para encontrar o crescimento por ano, podemos dividir: 3000 alce / 4 anos = 750 alce em 1 ano.

Alternativamente, pode-se usar a fórmula de inclinação da álgebra para determinar a diferença comum, observando que a população é a saída da fórmula, e o tempo é a entrada.

>

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{15,000-12,000}{2007-2003}=\frac{3000}{4}=750

Agora podemos escrever a nossa equação na forma que for preferida.

Forma recursiva

P0 = 12.000

Pn = Pn-1 + 750

Forma explícita

Pn = 12.000 + 750(n)

Para responder à pergunta, precisamos primeiro notar que o ano 2014 será n = 11, já que 2014 é 11 anos depois de 2003. O formulário explícito será mais fácil de usar para este cálculo:

P11 = 12.000 + 750(11) = 20.250 elk

Veja mais sobre este exemplo aqui.

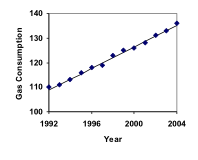
O consumo de gasolina nos EUA tem aumentado constantemente. Os dados de consumo de 1992 a 2004 são mostrados abaixo. Encontre um modelo para estes dados, e use-o para prever o consumo em 2016. Se a tendência continuar, quando é que o consumo atingirá 200 bilhões de galões?

Ano ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Consumo (biliões de galões) 110 111 113 116 118019> 118019> 119 123 125 126 128 131 133 136
Mostrar solução

Plotar estes dados, parece ter uma relação aproximadamente linear:

Embora existam técnicas estatísticas mais avançadas que podem ser usadas para encontrar uma equação para modelar os dados, para ter uma idéia do que está acontecendo, podemos encontrar uma equação usando duas partes dos dados – talvez os dados de 1993 e 2003.

Letar n = 0 corresponde a 1993 daria P0 = 111 bilhões de galões.

Para encontrar d, precisamos saber quanto o consumo de gás aumentou a cada ano, em média. De 1993 a 2003, o consumo de gás aumentou de 111 bilhões de galões para 133 bilhões de galões, uma variação total de 133 – 111 = 22 bilhões de galões, em 10 anos. Isto nos dá uma mudança média de 22 bilhões de galões / 10 anos = 2,2 bilhões de galões por ano.2 bilhões de galões por ano

Agora podemos escrever nossa equação em qualquer forma preferida.

Forma recursiva

P0 = 111

Pn = Pn-1 + 2.2

Forma explícita

Pn = 111 + 2.2n

Calcular valores usando a forma explícita e plotá-los com os dados originais mostra o quão bem o nosso modelo se encaixa nos dados.

Podemos agora usar o nosso modelo para fazer previsões sobre o futuro, assumindo que a tendência anterior continua inalterada. Para prever o consumo de gasolina em 2016:

n = 23 (2016 – 1993 = 23 anos depois)

P23 = 111 + 2,2(23) = 161,6

O nosso modelo prevê que os EUA consumirão 161.6 bilhões de galões de gasolina em 2016 se a tendência atual continuar.

Para descobrir quando o consumo chegará a 200 bilhões de galões, definiríamos Pn = 200, e resolveríamos para n:

Pn = 200 Substituir Pn pelo nosso modelo

111 + 2.2n = 200 Subtrair 111 de ambos os lados

2,2n = 89 Dividir ambos os lados por 2,2

n = 40,4545

Isto nos diz que o consumo chegará a 200 bilhões cerca de 40 anos depois de 1993, o que seria no ano 2033.

Os passos para alcançar esta resposta estão detalhados no seguinte vídeo.

O custo, em dólares, de uma inscrição num ginásio durante n meses pode ser descrito pela equação explícita Pn = 70 + 30n. O que nos diz esta equação?

Mostrar Solução

O valor para P0 nesta equação é 70, portanto o custo inicial de partida é de $70. Isto nos diz que deve haver uma taxa inicial ou inicial de $70 para entrar na academia.

O valor para d na equação é 30, então o custo aumenta em $30 a cada mês. Isto nos diz que a taxa mensal de inscrição no ginásio é de $30 por mês.

A explicação para este exemplo está detalhada abaixo.

Try It

O número de pais que ficam em casa no Canadá tem crescido constantemente. Embora a tendência não seja perfeitamente linear, ela é bastante linear. Use os dados de 1976 e 2010 para encontrar uma fórmula explícita para o número de pais que ficam em casa, depois use-a para prever o número em 2020.

Ano 1976 1984 1991 2000 2010
# de Stay -at-home fathers 20610 28725 43530 47665 53555
Mostrar Solução

Definir n= 0 corresponder a 1976, então P_0= 20.610.
De 1976 a 2010 o número de pais que ficaram em casa aumentou 53.555 – 20.610 = 32.945
Isto aconteceu durante 34 anos, dando um d diferente comum de 32.945 / 34 = 969.
P_n= 20.610 + 969n
Previsão para 2020, usamos n = 44, P(44) = 20.610 + 969(44) = 63.246 pais que ficaram em casa em 2020.

Quando os bons modelos vão mal

Ao usar modelos matemáticos para prever o comportamento futuro, é importante ter em mente que muito poucas tendências continuarão indefinidamente.

Exemplo

Suponha que um menino de quatro anos de idade tenha atualmente 39 polegadas de altura, e é dito a você para esperar que ele cresça 2,5 polegadas por ano.

Podemos montar um modelo de crescimento, com n = 0 correspondente a 4 anos de idade.

Forma recursiva

P0 = 39

Pn = Pn-1 + 2,5

Forma explícita

Pn = 39 + 2.5(n)

Assim, aos 6 anos de idade, esperaríamos que ele estivesse

P2 = 39 + 2,5(2) = 44 polegadas de altura

Aquilo modelo matemático acabará por se decompor. Certamente, não devemos esperar que este rapaz continue a crescer ao mesmo ritmo durante toda a sua vida. Se ele crescesse, aos 50 anos ele seria

P46 = 39 + 2.5(46) = 154 polegadas de altura = 12.8 pés de altura!

Ao usar qualquer modelo matemático, temos que considerar quais inputs são razoáveis para usar. Sempre que extrapolamos, ou fazemos previsões para o futuro, estamos assumindo que o modelo continuará válido.

Veja uma explicação em vídeo dessa quebra do modelo de crescimento linear aqui.

Crescimento experimental (Geométrico )

Crescimento da população

Suponha que a cada ano, apenas 10% dos peixes de um lago têm filhotes sobreviventes. Se houvesse 100 peixes no lago no ano passado, haveria agora 110 peixes. Se houvesse 1000 peixes no lago no ano passado, haveria agora 1100 peixes. Sem nenhum fator inibidor, as populações de pessoas e animais tendem a crescer em um percentual da população existente a cada ano.


Ponha que nosso lago começou com 1000 peixes, e 10% dos peixes têm filhotes sobreviventes a cada ano. Desde que começamos com 1000 peixes, P0 = 1000. Como calculamos P1? A nova população será a população antiga, mais 10% adicionais. Simbolicamente:

P1 = P0 + 0.10P0

Notem que isto poderia ser condensado para uma forma mais curta pelo factoring:

P1 = P0 + 0.10P0 = 1P0 + 0.10P0 = (1+ 0.10)P0 = 1.10P0

Enquanto 10% é a taxa de crescimento, 1.10 é o multiplicador de crescimento. Note que 1,10 pode ser pensado como “os 100% originais mais 10% adicionais”

Para a nossa população de peixes,

P1 = 1,10(1000) = 1100

Podemos então calcular a população em anos posteriores:

P2 = 1.10P1 = 1.10(1100) = 1210

P3 = 1.10P2 = 1.10(1210) = 1331

Nota que no primeiro ano, a população cresceu em 100 peixes; no segundo ano, a população cresceu em 110 peixes; e no terceiro ano, a população cresceu em 121 peixes.

Embora haja um crescimento percentual constante, o aumento real do número de peixes está aumentando a cada ano.

Grafando estes valores vemos que este crescimento não parece linear.

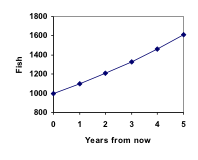
Um passeio por este cenário de peixes pode ser visto aqui:

Para obter uma melhor imagem de como este crescimento baseado na percentagem afecta as coisas, precisamos de uma forma explícita, para que possamos rapidamente calcular valores mais à frente no futuro.

Como fizemos para o modelo linear, vamos começar a construir a partir da equação recursiva:

P1 = 1.10(P0 )= 1.10(1000)

P2 = 1.10(P1 )= 1.10(1.10(1000)) = 1.102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Observando um padrão, podemos generalizar a forma explícita a ser:

Pn = 1.10n(1000), ou equivalente, Pn = 1000(1.10n)

A partir daí, podemos calcular rapidamente o número de peixes em 10, 20 ou 30 anos:

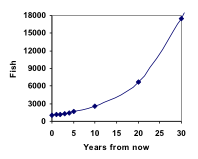
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Adicionar estes valores ao nosso gráfico revela uma forma que definitivamente não é linear. Se a nossa população de peixes tivesse crescido linearmente, em 100 peixes por ano, a população teria atingido apenas 4000 em 30 anos, em comparação com quase 18.000 com este crescimento percentual, chamado crescimento exponencial.

Um vídeo demonstrando o modelo explícito desta história de peixes pode ser visto aqui:

No crescimento exponencial, a população cresce proporcionalmente ao tamanho da população, de modo que à medida que a população aumenta, a mesma porcentagem de crescimento irá produzir um crescimento numérico maior.

Crescimento exponencial

Se uma quantidade começa no tamanho P0 e cresce por R% (escrito como decimal, r) a cada período de tempo, então a quantidade após n períodos de tempo pode ser determinada usando qualquer uma dessas relações:

Forma recursiva

Pn = (1+r) Pn-1

Forma explícita

Pn = (1+r)n P0 ou equivalente, Pn = P0 (1+r)n

Chamaremos r a taxa de crescimento.

O termo (1+r) é chamado de multiplicador de crescimento, ou razão comum.

Exemplo

Entre 2007 e 2008, Olympia, WA cresceu quase 3% para uma população de 245 mil pessoas. Se esta taxa de crescimento continuasse, qual seria a população de Olympia em 2014?

Mostrar Solução

Como fizemos antes, precisamos primeiro definir que ano corresponderá a n = 0. Como conhecemos a população em 2008, faria sentido ter 2008 correspondendo a n = 0, então P0 = 245.000. O ano 2014 seria então n = 6,

Sabemos que a taxa de crescimento é de 3%, dando r = 0,03,

Utilizando a forma explícita:

P6 = (1+0,03)6 (245.000) = 1,19405(245.000) = 292.542,25

O modelo prevê que em 2014, Olympia teria uma população de cerca de 293 mil pessoas.

O vídeo seguinte explica este exemplo em detalhe.

Avaliar expoentes na calculadora

Para avaliar expressões como (1,03)6, será mais fácil usar uma calculadora do que multiplicar 1,03 por si só seis vezes. A maioria das calculadoras científicas tem um botão para expoentes. É tipicamente rotulada como:

^ , yx , ou xy .

Para avaliar 1.036 nós escreveríamos 1.03 ^ 6, ou 1.03 yx 6. Experimente – você deve obter uma resposta em torno de 1.1940523.

Try It

India é o segundo país mais populoso do mundo, com uma população em 2008 de cerca de 1,14 bilhões de pessoas. A população está crescendo cerca de 1,34% a cada ano. Se esta tendência continuar, a população da Índia crescerá até 2020?

Mostrar Solução

Using n = 0 correspondente a 2008, P_12= (1+0,0134)12(1,14) = cerca de 1.337 bilhões de pessoas em 2020

Exemplos

Um amigo está usando a equação Pn = 4600(1.072)n para prever a mensalidade anual em uma faculdade local. Ela diz que a fórmula é baseada em anos após 2010. O que esta equação nos diz?

Mostrar Solução

Na equação, P0 = 4600, que é o valor inicial da anuidade quando n = 0. Isto nos diz que a anuidade em 2010 foi de $4.600,

O multiplicador de crescimento é 1,072, portanto a taxa de crescimento é de 0,072, ou 7,2%. Isso nos diz que a mensalidade deve crescer 7,2% a cada ano.

Pondo isso junto, podemos dizer que a mensalidade em 2010 foi de $4.600, e espera-se que cresça 7,2% a cada ano.

Veja o seguinte para ver este exemplo trabalhado.

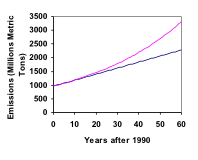
Em 1990, o uso de energia residencial nos EUA foi responsável por 962 milhões de toneladas métricas de emissões de dióxido de carbono. No ano 2000, esse número tinha aumentado para 1182 milhões de toneladas métricas. Se as emissões crescerem exponencialmente e continuarem no mesmo ritmo, o que as emissões crescerão até 2050?

Mostrar Solução

Similar a antes, corresponderemos n = 0 com 1990, já que esse é o ano para o primeiro dado que temos. Isso fará P0 = 962 (milhões de toneladas métricas de CO2). Neste problema, não nos é dada a taxa de crescimento, mas sim que P10 = 1182.

Quando n = 10, a equação explícita parece:

P10 = (1+r)10 P0

Sabemos o valor para P0, então podemos colocar isso na equação:

P10 = (1+r)10 962

Sabemos também que P10 = 1182, substituindo isso em, obtemos

1182 = (1+r)10 962

Agora podemos resolver esta equação para a taxa de crescimento, r. Comece dividindo por 962.

\frac{1182}{962}={{{(1+r)}^{10}} Pegue a 10ª raiz de ambos os lados

\sqrt{\frac{\1182}{962}}=1+r Subtraia 1 de ambos os lados

r=\sqrt{\frac{\1182}{962}}-1=0,0208 = 2,08%

Então se as emissões estão crescendo exponencialmente, elas estão crescendo em cerca de 2,08% por ano. Podemos agora prever as emissões em 2050 encontrando P60

P60 = (1+0,0208)60 962 = 3308,4 milhões de toneladas métricas de CO2 em 2050

Veja mais sobre este exemplo aqui.

Rounding

Como uma nota sobre arredondamento, note que se tivéssemos arredondado a taxa de crescimento para 2,1%, nosso cálculo para as emissões em 2050 teria sido 3347. O arredondamento para 2% teria alterado nosso resultado para 3156. Uma diferença muito pequena nas taxas de crescimento se amplia muito no crescimento exponencial. Por este motivo, é recomendado arredondar a taxa de crescimento o mínimo possível.

Se precisar arredondar, mantenha pelo menos três dígitos significativos – números após qualquer zeros à esquerda. Assim, 0,4162 pode ser razoavelmente arredondado para 0,416. Uma taxa de crescimento de 0,001027 poderia ser razoavelmente arredondada para 0,00103,

Avaliar raízes na calculadora

No exemplo anterior, tivemos de calcular a 10ª raiz de um número. Isto é diferente de tomar a raiz quadrada básica, √. Muitas calculadoras científicas têm um botão para raízes gerais. É tipicamente rotulado como:

\sqrt{x}

Para avaliar a 3ª raiz de 8, por exemplo, ou digitaríamos 3 \sqrt{{{}}. 8, ou 8 {}sqrt{} 3, dependendo da calculadora. Tente na sua para ver qual usar – você deve obter uma resposta de 2.

Se a sua calculadora não tiver um botão raiz geral, nem tudo está perdido. Você pode usar a propriedade dos expoentes que diz que:

\sqrt{a}={a}^{\frac{1}{2}}.

Então, para calcular a 3ª raiz de 8, você poderia usar a chave do expoente da sua calculadora para avaliar 81/3. Para isso, digite:

8 yx ( 1 ÷ 3 )

Os parênteses dizem à calculadora para dividir 1/3 antes de fazer o expoente.

Try It

O número de usuários em uma rede social era de 45 mil em fevereiro, quando eles se tornaram públicos oficialmente, e cresceu para 60 mil em outubro. Se o site está crescendo exponencialmente, e o crescimento continua no mesmo ritmo, quantos usuários devem esperar dois anos depois de terem se tornado públicos?

Mostrar Solução

Aqui vamos medir n em meses e não anos, com n = 0 correspondendo ao mês de fevereiro quando se tornaram públicos. Isto dá P_0= 45 mil. Outubro é 8 meses depois, portanto P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\texto{ ou }3,66%
A equação geral explícita é P_n =(1.0366)^{n}45. Prevendo 24 meses depois de tornarem-se públicas dá P_{24}=(1.0366)^{24}45=106.63 mil usuários.

Exemplo

Vejamos o último exemplo, para efeitos de comparação, quais seriam as emissões de carbono em 2050 se as emissões crescerem linearmente ao mesmo ritmo?

Mostrar solução

Ganho obteremos n = 0 corresponde a 1990, dando P0 = 962. Para encontrar d, poderíamos adotar a mesma abordagem de antes, observando que as emissões aumentaram em 220 milhões de toneladas métricas em 10 anos, dando uma diferença comum de 22 milhões de toneladas métricas a cada ano.

Alternativamente, poderíamos usar uma abordagem semelhante à que usamos para encontrar a equação exponencial. Quando n = 10, a equação linear explícita se parece com:

P10 = P0 + 10d

Sabemos o valor para P0, então podemos colocar isso na equação:

P10 = 962 + 10d

Desde que sabemos que P10 = 1182, substituindo que em nós obtemos

1182 = 962 + 10d

Agora podemos resolver esta equação para a diferença comum, d.

1182 – 962 = 10d

220 = 10d

d = 22

Isso nos diz que se as emissões estão mudando linearmente, elas estão crescendo em 22 milhões de toneladas métricas a cada ano. Prevendo as emissões em 2050,

P60 = 962 + 22(60) = 2282 milhões de toneladas métricas.

Vai notar que este número é substancialmente menor do que a previsão do modelo de crescimento exponencial. Calcular e plotar mais valores ajuda a ilustrar as diferenças.

Uma demonstração deste exemplo pode ser vista no vídeo seguinte.

Então como sabemos qual modelo de crescimento usar quando se trabalha com dados? Há duas abordagens que devem ser usadas em conjunto sempre que possível:

  1. Encontrar mais de dois pedaços de dados. Traçar os valores, e procurar uma tendência. Os dados parecem estar mudando como uma linha, ou os valores parecem estar se curvando para cima?
  2. Considerar os fatores que contribuem para os dados. São coisas que você esperaria mudar linearmente ou exponencialmente? Por exemplo, no caso das emissões de carbono, poderíamos esperar que, na ausência de outros fatores, eles estariam intimamente ligados aos valores populacionais, que tendem a mudar exponencialmente.

By: adminPosted on

Deixe uma resposta

O seu endereço de email não será publicado.