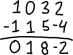Vissza a leckék indexéhez | A leckék sorrendben | Nyomtatásbarát oldal
Mátrixsor-műveletek (1. oldal a 2-ből)
A “műveletek” matematikai nyelven “eljárások”. A számokkal végzett négy “alapművelet” az összeadás, kivonás, szorzás és osztás. A mátrixok esetében három alapvető sorművelet létezik; vagyis három olyan eljárás van, amelyet egy mátrix soraival végezhetünk.
Az első művelet a sorváltás. Adott például a következő mátrix:

…felcserélhetjük a sorokat, hogy a mátrixot szebb sorelrendezésbe hozzuk, például így:
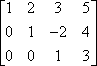
A sorváltást gyakran nyilak rajzolásával jelezzük, például így:

A sorok felcserélésekor ügyeljünk a bejegyzések helyes másolására.
A második művelet a sorszorzás. Adott például a következő mátrix:

…az első sort -1-gyel szorozhatjuk, hogy pozitív előjelű értéket kapjunk az első sorban:
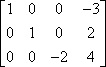
Ezt a sorszorzást gyakran egy nyíllal jelezzük, amelynek tetején a szorzás szerepel, így:
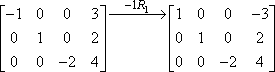
A “-1R1” jelzi a tényleges műveletet. A “-1” azt mondja, hogy negatív eggyel szoroztunk; az “R1” pedig azt, hogy az első sorral dolgoztunk. Figyeljük meg, hogy a második és harmadik sort változatlanul lemásoltuk a második mátrixba. A szorzás csak az első sorra vonatkozott, így a másik két sor bejegyzéseit változatlanul továbbvittük.
Azzal szorzunk, amivel akarunk. Például, hogy az előző mátrix harmadik sorában egy vezető 1-est kapjunk, megszorozhatjuk a harmadik sort negatív másféllel:

Mivel nem csináltunk semmit az első és a második sorral, azok a bejegyzések változatlanul átmásolódtak az új mátrixba.
Egy lépésen belül több sorszorozást is végezhetsz, így a fenti két lépést egyetlen lépésben is elvégezhetted volna, például így:
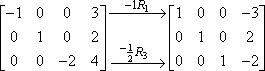
Azért érdemes valamilyen jelölést használni (például a fenti nyilakat és indexeket), hogy nyomon tudd követni a munkádat. A mátrixok nagyon rendetlenek, különösen, ha kézzel csinálod őket, és a jegyzetek megkönnyíthetik a munkád későbbi ellenőrzését. A tanárodat is lenyűgözi majd.
Az utolsó soros művelet a soros összeadás. A soros összeadás hasonló a lineáris egyenletrendszerek megoldására szolgáló “összeadás” módszeréhez. Tegyük fel, hogy a következő egyenletrendszered van:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Adalék
A rendszer megoldását az oszlopok összeadásával kezdheted, hogy 4y = 4 legyen:
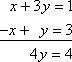
Mátrixokkal valami hasonlót tehetsz.Adott például a következő mátrix:

…a második sort úgy tudod “csökkenteni” (több vezető nullát kapni), hogy hozzáadod az első sort (a mátrixoknál ilyenkor az az általános cél, hogy minden mátrixsor elején legyen egy “1” – vagy “0-k”, majd egy “1” -). Amikor a két egyenletből álló lineáris rendszert összeadással csökkentetted, akkor egy “egyenlő” sávot húztál az aljára, és lefelé adtál össze. Amikor összeadást használsz egy mátrixon, akkor kapj fel egy kis karcolópapírt, mert nem akarod megpróbálni a munkát a mátrixon belül elvégezni. Add össze tehát a két sort a karcolópapírodon:
|
Karcolómunka – |
|
Ez az új második sorod; a régi második sor helyére fogod írni. Az eredmény így fog kinézni:
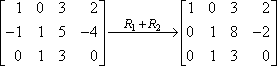
A nyílra írt “R1 + R2” ebben az esetben azt jelenti, hogy “az első sort hozzáadtam a második sorhoz, és ezt az eredményt kaptam”. Mivel az egyes sor valójában nem változott, és mivel a hármas sorral nem csináltunk semmit, ezek a sorok változatlanul átmásolódnak az új mátrixba.
Top | 1 | 2 | Vissza az indexhez Következő >>
|
Citálja ezt a cikket: |
Stapel, Elizabeth. “Mátrixsor-műveletek”. Purplemath. Elérhető: 2016
|
.