Klasszifikáció diszkriminanciaanalízissel
Lássuk, hogyan vezethető le az LDA mint felügyelt osztályozási módszer. Tekintsünk egy általános osztályozási problémát: Egy X véletlen változó K osztály valamelyikéből származik, néhány osztályspecifikus valószínűségi sűrűséggel f(x). Egy diszkriminancia-szabály megpróbálja az adattér K diszjunkt régióra osztani, amelyek az összes osztályt reprezentálják (képzeljük el a dobozokat egy sakktáblán). Ezekkel a régiókkal a diszkriminanciaelemzéssel történő osztályozás egyszerűen azt jelenti, hogy x-et a j osztályba soroljuk, ha x a j régióba esik. A kérdés tehát az, hogy honnan tudjuk, hogy az x adat melyik régióba esik? Természetesen két kiosztási szabályt követhetünk:
- Maximum likelihood szabály: Ha feltételezzük, hogy minden osztály azonos valószínűséggel fordulhat elő, akkor az x-et a j osztályba soroljuk, ha
- Bayes-szabály: Ha ismerjük az osztályok előzetes valószínűségeit, π, akkor rendeljük x-et a j osztályba, ha

Lineáris és kvadratikus diszkriminanciaanalízis
Ha feltételezzük, hogy az adatok többváltozós Gauss-eloszlásból származnak, i.azaz X eloszlása jellemezhető az átlagával (μ) és a kovarianciájával (Σ), akkor a fenti kiosztási szabályok explicit formáit kaphatjuk. A Bayes-szabály szerint az x adatot akkor soroljuk a j osztályba, ha i = 1,…,K esetén az összes K osztály közül a legnagyobb valószínűséggel rendelkezik:

A fenti függvényt diszkriminanciafüggvénynek nevezzük. Figyeljük meg a log-likelihood használatát itt. Más szóval a diszkriminanciafüggvény megmondja, hogy az x adat milyen valószínűséggel tartozik az egyes osztályokba. A bármely két osztályt, k-t és l-t elválasztó döntési határ tehát az x azon halmaza, ahol a két diszkriminanciafüggvény értéke megegyezik. Ezért minden olyan adat, amely a döntési határra esik, egyforma valószínűséggel származik a két osztályból (nem tudtunk dönteni).
A LDA abban az esetben merül fel, ha K osztály között egyenlő kovarianciát feltételezünk. Azaz osztályonként egy kovarianciamátrix helyett minden osztály azonos kovarianciamátrixú. Ekkor a következő diszkriminanciafüggvényt kapjuk:

Megjegyezzük, hogy ez egy lineáris függvény x-ben. Így a döntési határ bármely osztálypár között szintén egy lineáris függvény x-ben, innen a neve: lineáris diszkriminanciaanalízis. Az egyenlő kovariancia feltételezése nélkül a valószínűségben lévő kvadratikus tag nem szűnik meg, ezért a kapott diszkriminanciafüggvény egy kvadratikus függvény x-ben:

A döntési határ ebben az esetben kvadratikus x-ben. Ezt nevezzük kvadratikus diszkriminanciaanalízisnek (QDA).
Melyik a jobb? LDA vagy QDA?
A valós problémákban a populációs paraméterek általában ismeretlenek, és a gyakorló adatokból mint mintaátlagok és mintakovariancia-mátrixok alapján becsülnek. Bár a QDA az LDA-hoz képest rugalmasabb döntési határokat fogad be, a becslendő paraméterek száma is gyorsabban nő, mint az LDA esetében. Az LDA esetében (p+1) paraméterre van szükség a (2.) diszkriminanciafüggvény megkonstruálásához. Egy K osztályt tartalmazó probléma esetén csak (K-1) ilyen diszkriminanciafüggvényre lenne szükségünk, ha egy osztályt tetszőlegesen választanánk bázisosztálynak (az összes többi osztályból kivonva az alaposztály valószínűségét). Ezért az LDA esetében a becsült paraméterek teljes száma (K-1)(p+1).
Másrészt, a (3)-ban szereplő minden egyes QDA diszkriminanciafüggvényhez meg kell becsülni az átlagvektort, a kovarianciamátrixot és az osztályprioritást:
– Középérték: p
– Kovariancia: p(p+1)/2
– Osztály prior: 1
Hasonlóképpen, a QDA esetében (K-1){p(p+3)/2+1} paramétereket kell becsülnünk.
Ezért az LDA-ban a becsült paraméterek száma lineárisan nő p-vel, míg a QDA-ban négyzetesen nő p-vel. Azt várnánk, hogy a QDA rosszabb teljesítményt nyújt, mint az LDA, ha a probléma dimenziója nagy.
Két világ legjobbja? Kompromisszum az LDA & QDA
Az egyes osztályok kovariancia mátrixainak regularizálásával kompromisszumot találhatunk az LDA és a QDA között. A regularizálás azt jelenti, hogy a becsült paraméterekre bizonyos korlátozást helyezünk. Ebben az esetben megköveteljük, hogy az egyéni kovarianciamátrix egy büntetőparaméteren keresztül egy közös összevont kovarianciamátrix felé zsugorodjon, pl. α:

A közös kovarianciamátrixot szintén egy büntetőparaméteren keresztül egy azonossági mátrix felé regularizálhatjuk, pl., β:

Ahol a bemeneti változók száma jelentősen meghaladja a minták számát, ott a kovarianciamátrix rosszul becsülhető. A zsugorítás remélhetőleg javíthatja a becslés és az osztályozás pontosságát. Ezt szemlélteti az alábbi ábra.

Kiszámítás az LDA-hoz
A (2)-ből és (3)-ból láthatjuk, hogy a diszkriminanciafüggvények számítása egyszerűsíthető, ha először a kovariancia-mátrixokat diagonalizáljuk. Vagyis az adatokat úgy transzformáljuk, hogy identikus kovarianciamátrixot kapjunk (nincs korreláció, variancia 1). Az LDA esetében így járunk el a számítással:

A 2. lépésben gömbölyítjük az adatokat, hogy a transzformált térben identitás-kovarianciamátrixot kapjunk. A 4. lépés a (2)-t követve kapjuk meg.
Vegyünk egy kétosztályos példát, hogy lássuk, mit is csinál valójában az LDA. Tegyük fel, hogy két osztály van, k és l. Akkor soroljuk x-et a k osztályba, ha

A fenti feltétel azt jelenti, hogy a k osztályból nagyobb valószínűséggel származik x adat, mint az l osztályból. A fent vázolt négy lépést követve írjuk
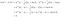
Azaz, az x adatot akkor soroljuk a k osztályba, ha

A levezetett kiosztási szabály felfedi az LDA működését. Az egyenlet bal oldala (l.h.s.) az x* ortogonális vetületének hossza a két osztályközepet összekötő egyenes szakaszra. A jobb oldal a szegmens középpontjának az osztályok előzetes valószínűségeivel korrigált helye. Lényegében az LDA a gömbölyített adatokat a legközelebbi osztályátlaghoz sorolja. Itt két megfigyelést tehetünk:
- A döntési pont eltér a középponttól, ha az osztályok előzetes valószínűségei nem azonosak, azaz a határ a kisebb előzetes valószínűségű osztály felé tolódik.
- Az adatokat az osztályátlagok által átfogott térre vetítjük (az x* szorzása és az átlag kivonása a szabály l.h.s.-én). A távolsági összehasonlításokat ezután ebben a térben végezzük.