Kémiai kinetika
Kémiai kinetika
Elképzelhető, hogy ismeri a fenolftaleint végpontindikátorként használó sav-bázis titrálásokat. Azt azonban talán még nem vetted észre, hogy mi történik, amikor a fenolftaleint tartalmazó oldatot felesleges bázis jelenlétében néhány percig állni hagyjuk. Bár az oldat kezdetben rózsaszínű, fokozatosan színtelenné válik, amint a fenolftalein reakcióba lép az erősen bázikus oldatban lévő OH-ionnal.
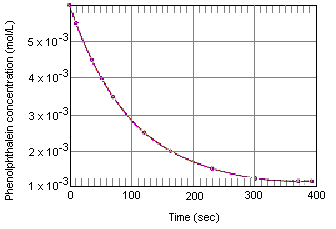
Az alábbi táblázat azt mutatja, hogy mi történik a fenolftalein koncentrációjával egy olyan oldatban, amely eredetileg 0,005 M fenolftaleint és 0,61 M OH-iont tartalmazott. Mint látható, amikor ezeket az adatokat az alábbi grafikonon ábrázoljuk, a fenolftaleinkoncentráció körülbelül négy perc alatt tízszeresére csökken.
Kísérleti adatok a fenolftalein és a bázisfelesleg közötti reakcióra
A fenti táblázatban szereplő adatokhoz hasonló kísérleteket a kémiai kinetika (a görög “mozog” jelentésű törzsből) méréseinek minősítik. E kísérletek egyik célja a reakció sebességének leírása, vagyis annak a sebességnek a leírása, amellyel a reaktánsok a reakció termékeivé alakulnak át.
A sebesség kifejezést gyakran használják egy mennyiségben időegység alatt bekövetkező változás leírására. Az inflációs ráta például egy szabványos cikkekből álló kollekció átlagos költségének évenkénti változása. A sebesség, amellyel egy tárgy a térben halad, az időegységenként megtett távolság, például mérföld/óra vagy kilométer/másodperc. A kémiai kinetikában a megtett távolság a reakció egyik komponensének koncentrációjában bekövetkező változás. A reakció sebessége tehát az egyik reaktáns![]() (X)
(X)![]() koncentrációjának változása
koncentrációjának változása![]() t adott idő alatt.
t adott idő alatt.
![]()
1. gyakorlati feladat:
A fenti táblázat adatai alapján számítsuk ki, hogy a fenolftalein milyen sebességgel reagál az OH-ionnal az alábbi időszakok mindegyikében:
a) Az első időintervallum alatt, amikor a fenolftalein koncentrációja 0,0050 M-ről 0,0045 M-re csökken.
(b) A második időintervallum alatt, amikor a koncentráció 0,0045 M-ről 0,0040 M-re csökken.
(c) A harmadik időintervallum alatt, amikor a koncentráció 0,0040 M-ről 0,0035 M-re csökken.
Az 1. gyakorló feladatra adott válasz ellenőrzéséhez kattintson ide.
Kattints ide az 1. gyakorlati feladat megoldásának megtekintéséhez.
![]()
A reakciók pillanatnyi sebessége és a reakció sebességtörvénye
A fenolftalein és az OH-ion közötti reakció sebessége nem állandó, hanem idővel változik. Mint a legtöbb reakció, ennek a reakciónak a sebessége is fokozatosan csökken, ahogy a reaktánsok elfogynak. Ez azt jelenti, hogy a reakció sebessége mérés közben változik.
Az emiatt a méréseinkben fellépő hiba minimalizálása érdekében célszerűnek tűnik, hogy a reakciósebességet olyan időtartamokban mérjük, amelyek rövidek ahhoz az időhöz képest, amely alatt a reakció végbemegy. Megpróbálhatjuk például mérni azt a végtelenül kis koncentrációváltozást![]() d(X)
d(X)![]() , amely végtelenül rövid idő alatt következik be. Ezeknek a mennyiségeknek az arányát nevezzük a reakció pillanatnyi sebességének.
, amely végtelenül rövid idő alatt következik be. Ezeknek a mennyiségeknek az arányát nevezzük a reakció pillanatnyi sebességének.
![]()
A reakció pillanatnyi sebessége bármely időpontban kiszámítható a reaktáns (vagy termék) koncentrációjának az idő függvényében készített grafikonból. Az alábbi ábra azt mutatja, hogy a fenolftalein bomlásának reakciósebessége hogyan számítható ki a koncentráció és az idő grafikonjából. A reakciósebesség bármely időpillanatban egyenlő a görbéhez az adott pillanatban húzott érintő meredekségével.
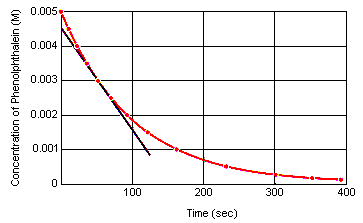
A reakció pillanatnyi sebessége mérhető a reaktánsok keveredése és a reakció egyensúlyba kerülése közötti bármely időpontban.Ha ezeket az adatokat visszavetítjük a reagensek keveredésének időpontjáig, megkapjuk a reakció kezdeti pillanatnyi sebességét.
![]()
Ráta-törvények és sebességállandók
Egy érdekes eredményt kapunk, ha a reakció pillanatnyi sebességét kiszámítjuk a görbe különböző pontjain az előző szakaszban szereplő grafikonon. A reakció sebessége a görbe minden pontján egyenesen arányos a fenolftalein koncentrációjával az adott pillanatban.
Ráta = k(fenolftalein)
Mert ez az egyenlet egy kísérleti törvény, amely leírja a reakció sebességét, ezért a reakció sebességtörvényének nevezzük. Az arányossági állandót, k-t, sebességállandónak nevezzük.
2. gyakorlati feladat:
Kalkulálja ki a fenolftalein és az OH-ion közötti reakció sebességállandóját, ha a reakció pillanatnyi sebessége 2,5 x 10-5 mol/liter/másodperc, amikor a fenolftalein koncentrációja 0,0025 M.
A 2. gyakorlati feladatra adott válaszának ellenőrzéséhez kattintson ide.
A 2. gyakorlati feladat megoldásának megtekintéséhez kattintson ide.
3. gyakorlati feladat:
A fenolftalein és az OH-ion közötti reakció sebességi állandóját felhasználva számítsa ki a reakció kezdeti pillanatnyi sebességét az előző táblázatban felsorolt kísérleti adatokra.
A 3. gyakorlati feladatra adott válaszának ellenőrzéséhez kattintson ide.
A 3. gyakorlati feladat megoldásának megtekintéséhez kattintson ide.
![]()
A reakció sebességének különböző kifejezési módjai
A reakció sebességének mérésére általában egynél több mód van. A hidrogén-jodid bomlását például úgy vizsgálhatjuk, hogy mérjük a sebességet, amellyel vagy H2 vagy I2 keletkezik a következő reakcióban, vagy azt a sebességet, amellyel a HI elfogy.
2 HI(g) H2(g) + I2(g)
Kísérletileg azt találjuk, hogy az I2 keletkezésének sebessége arányos a HI koncentráció négyzetével bármely időpontban.
![]()
Mi történne, ha megvizsgálnánk a H2 képződésének sebességét?Az egyensúlyi egyenlet azt sugallja, hogy a H2 és az I2 pontosan ugyanolyan sebességgel képződik.
![]()
Mi történne azonban, ha megvizsgálnánk a HI fogyásának sebességét ebben a reakcióban? Mivel a HI elfogy, a koncentrációváltozásnak negatív számnak kell lennie. A konvenció szerint a reakció sebességét mindig pozitív számként adjuk meg. Ezért meg kell változtatnunk az előjelet, mielőtt megadjuk a reakciósebességet a reakcióban elfogyó reakciótényezőre vonatkozóan.
![]()
A negatív előjel két dolgot tesz. Matematikailag a HI koncentrációjának negatív változását pozitív sebességgé alakítja át. Fizikailag arra emlékeztet, hogy a reaktáns koncentrációja az idővel csökken.
Milyen összefüggés van a H2 vagy I2 képződésének megfigyelésével kapott reakciósebesség és a HI eltűnésének megfigyelésével kapott sebesség között? A reakció sztöchiometriája szerint minden keletkező H2 vagy I2 molekulára két HI molekula jut. Ez azt jelenti, hogy a HI bomlási sebessége kétszer olyan gyors, mint a H2 és I2 keletkezésének sebessége. Ezt az összefüggést a következőképpen fordíthatjuk le matematikai egyenletre.
![]()
Az ebben a reakcióban a H2 és I2 keletkezésének sebességét vizsgálva kapott sebességállandó (k) nem azonos a HI fogyásának sebességét figyelve kapott sebességállandóval (k’)
gyakorlati feladat:
Kalkulálja ki, milyen sebességgel tűnik el a HI a következő reakcióban abban a pillanatban, amikor I2 keletkezik 1 sebességgel.8 x 10-6 mol/liter/másodperc:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
A 4. gyakorlati feladatra adott válasz ellenőrzéséhez kattintson ide.
A 4. gyakorlati feladat megoldásának megtekintéséhez kattintson ide.
![]()
A sebességtörvény és a reakció sztöchiometriája
Az 1930-as években Sir Christopher Ingold és munkatársai a University ofLondonban a következőhöz hasonló helyettesítési reakciók kinetikáját tanulmányozták.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Azt találták, hogy a reakció sebessége arányos a két reaktáns koncentrációjával.
Ráta = k(CH3Br)(OH-)
Amikor egy kicsit más kiindulási anyaggal hasonló reakciót végeztek, hasonló termékeket kaptak.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
De most a reakció sebessége csak az egyik reaktáns koncentrációjával volt arányos.
Ráta = k((CH3)3CBr)
Az eredmények egy fontos pontot szemléltetnek: A reakció sebességtörvénye nem jósolható meg a reakció sztöchiometriájából; azt kísérleti úton kell meghatározni. Néha a sebességtörvény összhangban van azzal, amit a reakció sztöchiometriájából várunk.
2 HI(g) H2(g) + I2(g)
Ráta = k(HI)2
Gyakran, azonban ez nem így van.
| 2 N2O5(g) |
Ráta = k(N2O5) |
![]()
Molekuláris sorrend
Egyes reakciók egy lépésben zajlanak. Az egylépéses reakcióra jó példa az a reakció, amelyben egy klóratom átkerül a ClNO2-ről a NO-ra, így NO2 és ClNO keletkezik.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Más reakciók több önálló lépés sorozatával zajlanak. Az N2O5 például háromlépéses mechanizmussal bomlik NO2-re és O2-re.
| 1. lépés: | N2O5 |
|
| 2. lépés: | NO2 + NO3 |
|
| 3. lépés: | NO + NO3 |
A reakció lépéseit molekularitás szerint osztályozzuk,ami a felhasznált molekulák számát írja le. Ha egyetlen molekula fogy el, a lépést egymolekulárisnak nevezzük. Ha két molekula fogy el, akkor bimolekuláris.
5. gyakorlati feladat:
Meghatározhatja az egyes lépések molekularitását abban a reakcióban, amelynek során az N2O5 NO2-re és O2-re bomlik.
Az 5. gyakorlati feladatra adott válaszának ellenőrzéséhez kattintson ide.
Az 5. gyakorlati feladat megoldásának megtekintéséhez kattintson ide.
A reakciókat a sorrendjük alapján is osztályozhatjuk. Az N2O5 bomlása elsőrendű reakció, mert a reakció sebessége az N2O5 első hatványra emelt koncentrációjától függ.
Ráta = k(N2O5)
A HI bomlása másodrendű reakció, mert a reakció sebessége a HI második hatványra emelt koncentrációjától függ.
Rate = k(HI)2
Ha egy reakció sebessége több reagenssel függ, akkor a reakciót az egyes reagensek sorrendje szerint osztályozzuk.
6. gyakorlati feladat:
Osszuk meg a NO és O2 között NO2 képződésével lejátszódó reakció sorrendjét:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Tegyük fel a következő sebességtörvényt erre a reakcióra:
Ráta = k(NO)2(O2)
A 6. gyakorlati feladatra adott válasz ellenőrzéséhez kattintson ide.
A reakció molekularitása és sorrendje közötti különbség fontos. Egy reakció molekuláris jellege, vagy egy reakción belüli lépés,azt írja le, hogy mi történik molekuláris szinten. A reakció sorrendje leírja, hogy mi történik makroszkopikus szinten. A reakció sorrendjét úgy határozzuk meg, hogy megfigyeljük a reakciótermékek megjelenését, illetve a reaktánsok eltűnését. A reakció molekuláris voltára következtetünk, hogy megmagyarázzuk ezeket a kísérleti eredményeket.
![]()
A kémiai reakciók ütközéselméleti modellje
A kémiai reakciók ütközéselméleti modellje felhasználható az egylépéses és többlépéses reakciók megfigyelt sebességtörvényeinek magyarázatára. Ez a modell abból indul ki, hogy a reakció bármely lépésének sebessége az adott lépésben részt vevő részecskék közötti ütközések gyakoriságától függ.
Az alábbi ábra az ütközéselméleti modell következményeinek megértéséhez nyújt alapot egyszerű, egylépéses reakciók esetében, mint például a következő.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
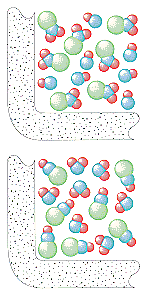
A kinetikus molekulaelmélet feltételezi, hogy a gázban a másodpercenkénti ütközések száma a részecskék literenkénti számától függ. Az NO2és ClNO képződésének sebessége ebben a reakcióban ezért egyenesen arányosnak kell lennie mind a ClNO2, mind a NO koncentrációjával.
Ráta = k(ClNO2)(NO)
Az ütközéselméleti modell szerint a reakció bármely lépésének sebessége arányos az adott lépésben elfogyasztott reagensek koncentrációjával. Az egylépéses reakció sebességtörvényének ezért meg kell egyeznie a reakció sztöchiometriájával.
A következő reakció például egyetlen lépésben játszódik le.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Amikor ezek a molekulák a megfelelő orientációban ütköznek, az OH- ionon egy pár nemkötő elektron adható a CH3Br molekula középpontjában lévő szénatomnak, ahogy az alábbi ábrán látható.
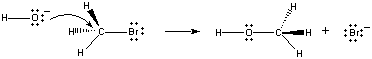
Amikor ez megtörténik, egy szén-oxigén kötés jön létre aszén-brom kötés felszakadásával egyidejűleg. Ennek a reakciónak a végeredménye az, hogy egyOH- ion helyett egy Br – ion keletkezik. Mivel a reakció egylépésben megy végbe, ami a két reaktáns közötti ütközésekkel jár, a reakció sebessége arányos a két reaktáns koncentrációjával.
Ráta = k(CH3Br)(OH-)
Nem minden reakció megy végbe egy lépésben. A következő reakció három lépésben megy végbe, ahogy az alábbi ábrán látható.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
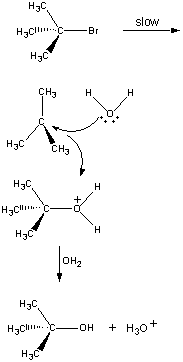
Az első lépésben a (CH3)3CBr molekula egy ionpárra disszociál.
| Első lépés | 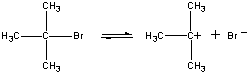 |
A pozitív töltésű (CH3)3C+ ion ezutána második lépésben reakcióba lép a vízzel.
| Második lépés | 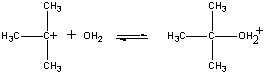 |
A reakció terméke ezután az utolsó lépésben elveszít egy protont az OH-ionnak vagy a víznek.
| Harmadik lépés | 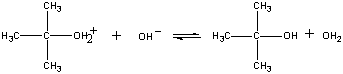 |
E reakció második és harmadik lépése nagyon sokkal gyorsabb, mintaz első.
| (CH3)3CBr |
Lassú lépés | |
| (CH3)3C+ + H2O |
Gyors lépés | |
| (CH3)3COH2+ + OH- |
Gyors lépés |
A teljes reakciósebesség tehát nagyjából megegyezik az első lépés sebességével. Az első lépést ezért sebességkorlátozó lépésnek nevezzük ebben a reakcióban, mert szó szerint korlátozza azt a sebességet, amellyel a reakció termékei képződhetnek. Mivel a sebességkorlátozó lépésben csak egy reagens vesz részt, a reakció összsebessége csak ennek a reagensnek a koncentrációjával arányos.
sebesség = k((CH3)3CBr)
A reakció sebességtörvénye tehát eltér attól, amit a reakció sztöchiometriája alapján feltételeznénk. Bár a reakcióban mind a (CH3)3CBr,mind az OH- felhasználásra kerül, a reakció sebessége csak a(CH3)3CBr koncentrációjával arányos.
A kémiai reakciók sebességtörvényei a következő általános szabályokkal magyarázhatók.
A reakció bármely lépésének sebessége egyenesen arányos az adott lépésben felhasznált reagensek koncentrációjával.
A reakció általános sebességtörvényét azoknak a lépéseknek a sorozata, vagyis a mechanizmus határozza meg, amelyekkel a reaktánsok a reakció termékeivé alakulnak át.
A reakció általános sebességtörvényét a reakció leglassabb lépésének sebességtörvénye uralja.