Valószínűség > Hátsó valószínűség & a hátsó eloszlás
Mi a hátsó valószínűség?
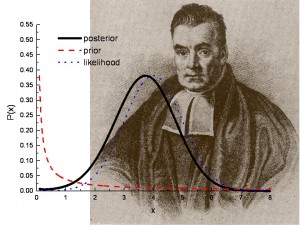
A hátsó valószínűségeket a bayesi hipotézisvizsgálatban használják. Kép: Los Alamos National Lab.
A poszterior valószínűség egy esemény bekövetkezésének valószínűsége, miután minden bizonyítékot vagy háttérinformációt figyelembe vettünk. Szorosan kapcsolódik az előzetes valószínűséghez, amely az a valószínűség, hogy egy esemény bekövetkezik, mielőtt bármilyen új bizonyítékot figyelembe vennénk. Az utólagos valószínűségre úgy is gondolhatunk, mint az előzetes valószínűség kiigazítására:
A történelmi adatok szerint például az egyetemet megkezdő diákok körülbelül 60%-a 6 éven belül végez. Ez az előzetes valószínűség. Ön azonban úgy gondolja, hogy ez a szám valójában sokkal alacsonyabb, ezért új adatok gyűjtésére indul. Az összegyűjtött bizonyítékok azt sugallják, hogy a valódi adat valójában közelebb van az 50%-hoz; ez az utólagos valószínűség.
A kifejezések eredete
Az utólagos és a prior szavak a latin a priori szóból származnak. Az “a priori” definíciója:
“…azzal kapcsolatos, amit inkább bizonyos dolgok működésének megértése, mint megfigyelés útján lehet tudni.” ~ Miriam Webster.
A “a priori” ellentéte az a posteriori, amelyet így definiálnak:
“… relating to what can be known by observation rather than through an understanding of how certain things work” ~ Miriam Webster.
Mi az a posterior distribution?
A posterior distribution egy módja annak, hogy összefoglaljuk, mit tudunk a bizonytalan mennyiségekről a bayesi elemzésben. Ez az előzetes eloszlás és a valószínűségi függvény kombinációja, amely megmondja, hogy milyen információt tartalmaznak a megfigyelt adatok (az “új bizonyítékok”). Más szóval, az utólagos eloszlás összefoglalja, hogy mit tudunk az adatok megfigyelése után. Az új megfigyelésekből származó bizonyítékok összegzése a valószínűségi függvény.
A poszterior eloszlások létfontosságúak a Bayes-elemzésben. Sok szempontból az elemzés célját jelentik, és megadhatják:
- Intervallumbecsléseket paraméterekre,
- Pontbecsléseket paraméterekre,
- Prediction inference for future data,
- Hipotézisünk valószínűségi értékelését.
Stephanie Glen. “Posterior Probability & the Posterior Distribution” From StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!