Hány oldala van egy körnek?

Ez egy általános iskolai házi feladat kérdése, amely a tapasztalt matematikusok között is nézeteltérést okoz. A helyes válasz megtalálásához a legszigorúbb tudományos eszközt, a Twitter-felmérést hívtam segítségül:

Még utólag is sajnálom, hogy nem szerepeltettem a “egyik sem” opciót, de erről később. Ebben a bejegyzésben végigmegyek ezen a három válaszon (és a “egyik sem” válaszon), és megvitatom az előnyeiket és hátrányaikat, ahogy én látom őket, mielőtt drámai módon felfedném a helyes választ.

De először is: miért nem tudjuk egyenesen megadni a helyes választ? A kérdésben szereplő szavak aligha titokzatosak. Mindannyian tudjuk, mi az a “kör”, mit jelent az, hogy “hányat” számolunk valamiből, és mi az az “oldal”… vagy nem? Íme a (durva) definíciók, amelyeket két általános iskolás diákkal folytatott beszélgetésből desztilláltam ki, akiknek már volt dolguk ezzel a kérdéssel:

1. Egy vonal, amely egy síkbeli alakzat határának részét képezi.

Azért mondunk itt “alakzat” helyett síkbeli alakzatot, mert olyan alakzatokat akarunk, amelyek 2 dimenzióban élnek (pl. négyzet vagy kör, de nem gömb vagy kocka). A következő kérdés az, hogy mi az a “vonal” az 1. definícióban. Íme egy változat, amely ezt rögzíti:

2. Egy síkbeli alakzat határának részét képező egyenes vonal.

Ha beírjuk a Google-be, hogy “define: side”, a legmegfelelőbb definíció a következő:

A egyenes vonalú alakzat egyenes vonalakból épül fel. Ez a definíció tehát a 2. definíció továbbfejlesztése, és lehetővé teszi, hogy megerősítsük, hogy a négyzetnek négy oldala van, de látszólag nem mond semmit a nem egyenes vonalú síkbeli alakzatokról, például a körökről.

Végtelen sok oldal?

Azt hiszem, biztosra vehető, hogy a Twitter-felmérésemre válaszolóknak magasabb a matematikai végzettsége, mint az országos átlag. Az a tény, hogy egyáltalán megosztottak voltak ebben a kérdésben, és hogy egy kis többség olyan választ választott, amely eléggé elérhetetlen a kérdés szokásos célközönsége (általános iskolások) számára, minden bizonnyal arra utal, hogy valahol valami rosszul megy.

Szóval, egy körnek végtelen sok oldala van? Mindenképpen hasznos a kört az n oldalú sokszögek határértékének tekinteni, ahogy az n egyre nagyobb és nagyobb lesz. Pontosan ez az a megközelítés, amelyet Arkhimédész, Liu Hui és számtalan más ember használt az évszázadok során a körgeometria tanulmányozására, beleértve a π-re vonatkozó közelítéseket is.

A Jiuzhang suanshu (Kilenc fejezet a matematikai művészetről) XVI. századi, a Ming-dinasztia korabeli kiadása, Kr. u. III. század.

Néha teljesen ésszerű, mint kényelmes rövidítés, úgy gondolni a körre, mint egy végtelen sok oldalú sokszögre.

De mint elviselhetetlen pedáns matematikus, különbséget szeretnék tenni a kényelmes rövidítés és a szó szerinti igazság között. Ha ragaszkodunk ahhoz, hogy a kör valóban egy végtelen sok oldalú sokszög, akkor felmerül a kérdés: mik az oldalak? És bizonyára az egyetlen hihető válasz: a kör egyes pontjai. Milyen hosszúak ezek az úgynevezett oldalak? Nulla centiméter. És ezeket az oldalakat sarkok választják el egymástól? Nyilvánvalóan nem, vagy egyáltalán nincsenek sarkok, vagy minden pont egyszerre oldal és sarok.

Azt mondanám, hogy a nulla hosszúságú oldalak… problematikus fogalom. Honnan tudod megmondani, hogy van-e egyáltalán? Tegyük fel például, hogy egy olyan rendszert vizsgálok, ahol a négyzet a nyolcszögek határértékeként keletkezik, így:

Ebben a helyzetben talán van értelme úgy gondolnom a négyzetemre, hogy nyolc oldala van, amelyek közül négynek a hossza nulla. De ha ragaszkodnék ahhoz, hogy a (teljesen hétköznapi) négyzetemnek valóban nyolc oldala van, talán felhúznád a szemöldököd.”

Ez tehát – a szavazásom nyertes válasza – az egyetlen, amelyet véglegesen tévesnek fogok nyilvánítani, miközben ez az egyetlen, amely egyáltalán bármilyen geometriai meglátással szolgál. Paradoxon? Nem igazán. Az analógiás gondolkodás értékes készség a matematikában és az életben; ugyanakkor fontos, hogy ragaszkodjunk ahhoz a felismeréshez, hogy ezt tesszük.

A végtelen sok oldalra: geometriai megvilágítás.
Végtelenül sok oldalra: nyolcoldalú négyzetek.

Tangens 1: apeirogonok

Még ha a kör nem is az, léteznek-e végtelenül sok oldalú sokszögek? Nos, van egy szó az ilyenek leírására egy apeirogon. Egy szabályos apeirogon akkor egyenlő (nem nulla) hosszúságú oldalakkal rendelkezne, amelyek között egyenlő szögek vannak. Az egyetlen lehetőség itt ez a döbbenetesen izgalmatlan objektum:

Ha kifogásolod, hogy ez egy “sokszög” (vagy a 180°-os szögek, vagy a nem hurokban záródó élek láncolata miatt), mit szólnál valami ilyesmihez: kezdjük egy kör alján, és minden egyes lépésben haladjunk körbe a kör maradék felén, és az éppen megtett ívet cseréljük le egy egyenesre:

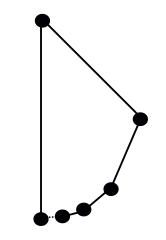
Ez egy valódi sokszög? Ez megint csak a fogalmaktól függ. Az egyik elterjedt definíció, a “zárt sokszöglánc” szerint ez nem felel meg, mivel a kezdő sarok (balra lent) csak egy élhez csatlakozik. De ez egy nagyon közeli hiba: ez a pont a jobbról jövő élek sorozatának határpontja, így ez az alakzat egy “nem önmetsző darabosan lineáris zárt görbe”, a sokszög másik, gyakran használt definíciója.

Ha elhagyjuk a megszokott euklideszi világunkat, és belépünk a hiperbolikus térbe, akkor nincs kétértelműség. Apeirogonok (sőt szabályos apeirogonok) egyszerűen léteznek:

A hiperbolikus sík szabályos apeirogonokkal való csempézése. (By Anton Sherwood – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extrém pontok

Talán védhetőbb lenne azt mondani, hogy egy körnek végtelen sok sarka van, mint végtelen sok oldala (bár ezt a kérdést, úgy tűnik, nem teszik fel túl gyakran). Kezdjük azzal, hogy ha egy négyzet sarka egy olyan pont, ahol a határvonala nem egyenes, akkor a kör minden pontja megfelel ennek. Még kifinomultabb módon létezik egy alakzat szélső pontjának fogalma: ez bármely olyan pont, amelyen keresztül olyan egyenes szakasz húzható, amely csak pontosan abban a pontban érinti az alakzatot. A négyzet és sok más ismert alakzat esetében a szélső pontok pontosan egybeesnek a sarkokkal. A kör határán minden pont szélső pont, tehát biztosan igaz, hogy a körnek végtelen sok van.

Elgondolkodhatunk azon, hogy néhány alakzatnak, például ennek az ékzárnak a sarkai nem szélső pontok:

Az alsó középső sarok nem szélső pont (a másik három sarok az). Az a baj, hogy ez az alakzat nem domború (nagyjából túlságosan kiálló részek vannak benne). A kör konvex, így talán nem kell aggódnunk. Alternatív megoldásként orvosolhatnánk a helyzetet, ha a “sarkot” olyan pontként definiálnánk, amely vagy a kérdéses alakzat, vagy annak komplementerének szélső pontja, azaz az egész síknak a kivágott alakzattal együtt. Ez a megközelítés minden sokszög sarkait felismerné, beleértve az ékzárat is. Sima görbék esetén minden határpontot “sarokként” azonosítana, kivéve az inflexiós pontokat (ami nem ésszerűtlen, hiszen ott azt állíthatnánk, hogy a határ egyenes).

Egy oldal?

Az általános iskolában úgy tűnik, hogy az “egy” az a válasz, amelyik megkapja a pipa. És van egy közepesen tisztességes indoklás. Emlékezzünk a fenti 1. definícióra:

1. Egy síkbeli alakzat határának részét képező vonal.

A közvetlen kérdés az, hogy mi számít “vonalnak”, különösen, ha nem ragaszkodunk az egyenességhez. Ha túlságosan lazák vagyunk ezzel kapcsolatban, akkor bármely síkbeli alakzatról azt mondhatjuk, hogy “egy oldala” van, ugyanabban az értelemben, ahogyan egy határa, kerülete vagy kerülete van. De ez biztosan rossz, hiszen biztosan azt akarjuk, hogy egy négyzetnek négy oldala legyen. Nos, egy négyzetnek négy olyan pontja van, ahol nem sima, és négy sima szakasza van a kettő között. Talán tényleg a sima szakaszokat számoltuk végig. Így implicit módon az 1. definíció új finomítása következik (és megragadjuk az alkalmat, hogy megszabaduljunk az “alakzat” homályos kifejezésétől):

4. Egy darabonként sima zárt görbe minden sima szakasza.

A “zárt görbe” olyan görbe, amely körbefordul, hogy találkozzon önmagával úgy, hogy nincsenek szabad végei. A “darabosan sima” azt jelenti, hogy sima szakaszokból épül fel, amelyek elszigetelt nem sima pontokban találkoznak. Teljesen jogos, ha egy ilyen alakzat határának sima szakaszait akarjuk megszámolni, és egyáltalán nem felháborító, ha ilyenkor az “oldal” szót használjuk. Tehát semmiképpen sem állítom, hogy ez véglegesen rossz válasz.

A kérdés az, hogy az “oldal” ilyen értelmezése nem pusztán koherens-e, hanem eléggé természetes-e ahhoz, hogy egyszerűen feltételezhető legyen anélkül, hogy kifejezetten kimondanánk (ami ritkán, vagy soha nem történik meg). Mi történik, ha a simaság és az egyenesség másképp áll össze? Tekintsük ezt a sírkőformát, amelyet úgy hoztunk létre, hogy egy négyzet tetejét egy egyenlő átmérőjű félkörrel helyettesítettük.

Ez két sima részből áll (az alsó vonal és a többi), de három egyenes éle van (plusz egy íves darab, amely kettőt simán összeköt). Hány oldala van tehát? Ismét konzultáltam a Twitter-barátaimmal:

Ezúttal a “végtelenül sok” opciót is fel kellett volna vennem, bár ez felszívható a “Semelyik sem” opcióba. Aki arra szavaz, hogy a körnek végtelenül sok oldala van, annak itt automatikusan a “Semmi a fentiek közül” opcióra kell szavaznia, hacsak – fontos kikötés – ennek az alakzatnak a természete nem jelzi az olvasó számára az “oldal” más fogalmát. Az a tény, hogy a legnépszerűbb választások ebben a két szavazásban nem összeegyeztethetőek, arra utal, hogy ez lehet a helyzet (vagy legalábbis megerősíti, hogy a vizek zavarosak).

Bár a kettő egy teljesen tiszteletreméltó válasz, amely összeegyeztethető a fenti 4. definícióval és a kör egyoldalúságával, nem vagyok meggyőződve arról, hogy véglegesen ez a helyes, vagy hogy a három vagy a négy kategorikusan rossz. Attól függ, hogy mit akarsz számolni: sima szakaszokat, egyenes éleket, vagy egyenes éleket plusz bármit, ami aztán megmarad, amelyek közül bármelyik lehet a kívánt válasz a kontextustól függően (erről bővebben alább). Ehhez kapcsolódóan nem vagyok benne biztos, hogy a sima szakaszok számának megszámlálása teljesen megfelel az intuíciómnak az “oldal” szóval kapcsolatban. Elvégre a sírkő két függőleges szakasza – szerintem joggal mondhatjuk – “ellentétes oldalon” van. Tényleg elégedettek vagyunk azzal, hogy ezek egyidejűleg “ugyanazon oldal” részei?

Tiltakozhatsz az ellen, hogy az “oldal” két különböző jelentését keverem össze, hogy a terminológia néha ütközik, és ezzel együtt kell élnünk. Én azonban nem vagyok ebben olyan biztos. Ennek a gyakorlatnak az a lényege, hogy egy olyan helyzetből (egyenes vonalú alakzatok) extrapoláljunk, ahol a két fogalom elég jól összefér. Ha lenne egy új ötlet, amely mindent megragadna, ami az eredetiben tetszett, de az alakzatok egy szélesebb kategóriájára is alkalmazható lenne, akkor ez lenne az elsöprő igény az egyedüli helyes válaszra. De ha minden általánosítási kísérletünk az eredeti kívánatos aspektusainak feláldozásával jár, akkor talán nincs egyetlen helyes általánosítás. Vannak különböző választások, különböző kompromisszumokkal, amelyek különböző kontextusokban megfelelőek lehetnek (és ha olyan helyzetben vagyunk, ahol egynél több is szóba jöhet, akkor hasznos lenne, ha különböző neveket adnánk nekik).

Itt egy másik variáció: egy Weierstrass-sírkő, amelyet úgy hozunk létre, hogy egy négyzet felső élét a Weiestress-függvény egy szakaszával helyettesítjük, egy végtelenül kacskaringós vonallal, amely sehol sem sima.

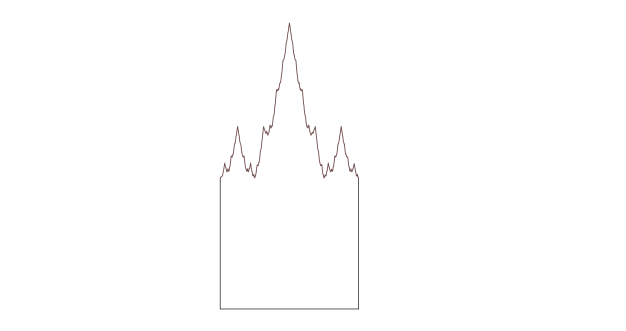
Íme (és figyeljétek meg a helyesírási hibát), amit Twitter-barátaim alkottak ebből – bár kevesebben mertek véleményt nyilvánítani:

Twitter-követőim szkepticizmusa ellenére mindjárt elmagyarázom, miért nem tartom ostobaságnak, hogy ennek négy oldala van (amelyek közül az egyik nem sima). Másrészt, ha jobban szereted a sima oldalakat, akkor megint csak választhatsz, hogy végtelen sok oldala van (amiből három 1 hosszúságú, a többi 0 hosszúságú), vagy 3 oldala van, plusz egy határozottan nem-oldalas határszakasz.

Egy oldalra: egyetlen sima görbe.
Egy oldalra: ugyanaz az oldal az ellentétes oldalakon.

Tangens 3: oldalak kontra élek

Hány oldala van egy négyzetnek? Négy. Hány éle van? Négy. Tehát az élek és az oldalak ugyanazok? Nem feltétlenül. Íme két konfiguráció, amelyek – legalábbis vitathatóan – mindegyike négyoldalú, de 5, illetve 3 élük van:

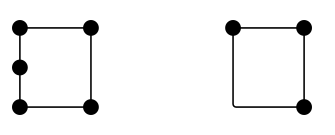
Az “él” általában azt mondanám, hogy egy “él” topológiai objektum, mivel a funkciója, nem pedig az alakja az, ami számít. Gondoljunk csak a londoni metró térképére. Ha azt kérdeznéd, hogy hány éle van annak a hálózatnak, akkor nincs értelme egyenes vagy sima szakaszokat összeszámolni. Az állomások (vagy csúcsok) közötti kapcsolatok számítanak.

Amint már említettük, a sokszögre általában úgy gondolunk, mint egy nagyon egyszerű hálózatra, amit zárt sokszögláncnak nevezünk: csúcsok (ebben az esetben a sokszög sarkainak) egy sora, élekkel összekötve, oly módon, hogy minden csúcs pontosan két élen fekszik, és az egész egy hurkot alkot. Ebben a helyzetben az élek és az oldalak, valamint a csúcsok és a sarkok egybeesnek. De általában meg lehet törni ezt az egybeesést, mint a fenti két kis hálózatban.

Ha hálózatelméletileg akarunk gondolkodni a dolgokról, de a csúcsok nincsenek egyértelműen jelölve, akkor ki kell találnunk, hogy hol vannak. Egy sokszög esetében ez könnyű – a csúcsok a sarkokban vannak -, ezért olyan természetes a váltás a geometriai és a topológiai megközelítések között. Más formák esetében azonban, mint például a fenti sírkövek bármelyike, ez nem biztos, hogy ilyen egyértelmű. Mindazonáltal mindegyik esetben, ha azt mondanák, hogy valahol vannak csúcspontok, és megkérnének, hogy keressük meg őket, azt hiszem, ésszerű lenne kitalálni, hogy négy van, nevezetesen az eredeti négyzet sarkai, és hogy a felső él valamilyen okból nem egyenes vonalként van ábrázolva. És ha valóban így akarunk gondolkodni, hogy minden egyes sírkőnek 4 széle van, akkor ez perverznek tűnhet (bár logikailag koherensnek!), hogy ragaszkodjunk ahhoz, hogy más oldalszámmal rendelkezzenek (különösen mivel a felső oldal – saját geometriája ellenére – egyértelműen az ábra “egyik oldalán” van). Sőt, találgatás helyett az egyik Twitter levelezőm azt kérdezte tőlem, hogy “Mindkét felső csúcsot eltávolították?”, aminek csak hálózatelméleti szempontból van értelme.

Hol marad a kör? Az a baj, hogy a kör egyetlen pontja sem tarthat jobb igényt arra, hogy csúcs legyen, mint bármelyik másik. Tehát bár csábító (és ismét koherens) a kört egy éllel rendelkező hálózatnak tekinteni, ha csúcspontokat akarunk beilleszteni, nincs nyilvánvaló okunk arra, hogy az egyiket előnyben részesítsük bármely más számmal szemben.

Nem tekinthetnénk egy olyan hálózatnak, amelynek egyáltalán nincsenek csúcsai, egyfajta metróvonalnak, amelynek nincsenek állomásai? A hálózat szokásos matematikai felfogása ezt nem engedné meg, de ez nem szabad, hogy túlságosan elriasszon minket. Ez egy tisztán topológiai megközelítést javasol. A baj az, hogy ebből a szempontból, míg egy kör lehet egyfajta hálózat csúcsok és egy él nélkül, addig egy négyzet is az (ha a metróvonal történetesen így van elrendezve). A topológiában a négyzet egy kör. (Ez nem paradoxon, egyszerűen csak azt mondja, hogy a határ egyetlen hurok, amelynek alakja nem számít.) Tehát míg egy ilyen hálózatnak “egy éle” van, addig egy négyzetnek nyilvánvalóan nincs “egy oldala”, így az oldalak (geometriai) és az élek (topológiai) közötti kapcsolat ismét felbomlott, akárcsak a fenti két kis hálózatban. Ez a megközelítés tehát nem visz minket túl messzire.

Nincsenek oldalak?

Paradoxnak tűnhet az az érvelés, hogy a körnek (vagy bármilyen alakzatnak) “nincsenek oldalai”. De a védekezés mellett szóló érv egyszerű. Térjünk vissza a 2. definícióhoz:

2. Egy síkbeli alakzat határának részét képező egyenes vonal.

Ez egy egyszerű, könnyen érthető kifejezés, amely tökéletesen megragadja a négyzet oldalait. Nem sikerült kielégítő általánosítást találnunk erre az íves alakzatokra, ezért a legjobb, ha maradunk az eredetinél. A körnek pedig nincsenek oldalai.

Az oldal nélkülire: igaz, az “oldal” értelmes fogalma szerint.
Az oldal nélkülire: úgy hangzik, mint egy zen koan.

A fentiek közül egyik sem?

Memlékezzünk a Google által megadott definícióra:

3. Egy sík egyenes vonalú alakzat határát alkotó vonalak mindegyike.

Az a kísérlet, hogy ezt egy körre – egy nem egyenes vonalú alakzatra – alkalmazzuk, nem eredményez semmit. A kérdés ugyanolyan értelmetlen, mint a “Hány oldala van a hétfőnek?”

Mivel a 3. definíció a leghivatalosabb (az egyetlen ebben a posztban, amit nem én vagy a gyerekeim találtak ki), nem jelenti ez kategorikusan azt, hogy “egyik sem” a helyes válasz? Talán. Másrészt: amikor valaki feltesz nekünk egy kérdést, a jótékonyság elve talán megköveteli, hogy feltételezzük, hogy értelmes, hacsak nem tudjuk határozottan megállapítani az ellenkezőjét, és az 1., 2., 4. definíciók és egyéb változatok ezt lehetővé teszik. Továbbá a 3. definíció inkább nyelvi, mint formailag matematikai, és ezért inkább leíró, mint előíró jellegű, tehát nem kellene elrejtőznünk mögötte.

A fentiek egyikéért sem: szemantikai hiba.
A fentiek egyikéért sem: dialogikus jótékonyság.

A helyes válasz

Mi késztetett arra, hogy megírjam ezt a bejegyzést? Számtalan általános iskoláshoz hasonlóan ötéves ikerfiaimnak – az elején említett általános iskolásoknak – nemrég ezt a kérdést tették fel a házi feladatban. Az egyikük az “1”-re, a másikuk a “0”-ra voksolt, és a fentiekben megpróbáltam megragadni és kibővíteni az érvelésüket. Szerintem mindkét válasz teljes mértékben védhető – és egyik sem véglegesen helyes.

Szóval, mit kell tenned, ha felteszik neked a kérdést: Hány oldala van egy körnek? Véleményem szerint az optimális válasz az, ha megkeresed életed matematikusát, hogy írjon egy 3000 szavas értekezést a témáról, amit aztán kinyomtatva diadalmasan átadhatsz szerencsétlen tanárodnak. De ha ez nem sikerül, a legjobb megközelítés, ha követed Szókratész példáját, és a kérdésre egy ellenkérdéssel válaszolsz:

Amikor mindent elmondunk, a nulláig vagy egyig való számolás, vagy a kérdés megválaszolásának megtagadása gyakorlatilag semmit sem mond nekünk a körök geometriájáról. De sokat nyerhetünk azzal, ha szétszedjük a megszokott fogalmakat, ha elhagyunk vagy hozzáadunk extra feltételeket, ha kihívás elé állítjuk az intuíciónkat azzal, hogy egy kontextusból egy kicsit más kontextusba lépünk, és megpróbáljuk pontosan leírni, hogy mit értünk egy adott fogalom alatt egy adott környezetben. Erről szól az igazi matematika.

Lábjegyzetek

Tehetnénk valami mást is: például választhatnánk egy P kiindulópontot a körön, ahonnan a kerület körüli távolságot mérjük. Ezután kijelenthetjük, hogy a P-től racionális távolságra lévő pontok a sarkok, a többi pedig az oldalak. Ez azt eredményezi, hogy megszámlálhatóan végtelen számú sarkot és megszámlálhatatlanul végtelen számú oldalt kapunk. Vagy megtehetjük az ellenkezőjét is. Ez kényelmesen illeszkedhet a körök poligonális határértékének megközelítéséhez, de nehezen tudnék egyetérteni azzal, hogy ez elég egyszerű vagy nyilvánvaló ahhoz, hogy “a helyes válasznak” tekintsük.

Egyik Twitter levelezőm aggódott amiatt, hogy mennyire sima a görbe. Ez a sírkő folyamatosan differenciálható, de nem kétszeresen. Bizonyára érdekes lenne, ha ezt sokan kritikus kérdésnek tartanák, és ezt valószínűleg lehetne tesztelni egy végtelenül sima sírkővel, amit valami ilyesmiből építettek, bár a részleteket még nem gondoltam végig.

Megpróbálhatnánk ezt a következőképpen megfogalmazni: egy négyzetben (vagy bármilyen sokszögben) egy oldalnak megvan az a tulajdonsága, hogy a belsejében lévő bármely helyről kiindulva az alakzatot egyenesen átvághatjuk a helyünkön, úgy, hogy a választott oldalunk szilárdan a vágás egyik oldalán legyen. Ez nem működik a kétoldalas sírkő esetében: bármilyen vágás mindig a hosszú oldalt fogja elvágni. Gyengíthetnénk ezt azzal, hogy ahhoz, hogy oldalnak számítson, legalább egy módon át kell vágni az alakzatot úgy, hogy az oldal a vágás egyik oldalán legyen. Ez lehetővé tenné számunkra, hogy azt mondjuk, hogy a sírkőnek négy oldala van (még akkor is, ha az íves szakasz nem a felső régió pontjainak egyik oldalán van). A kör esetében azonban a feltételezett egyik oldala soha nem egy oldalon van (így kizárható lenne), és csak a félkör egyenes szakasza számítana oldalnak.

Nem könnyű olyan szigorú indoklással előállni, ami mindkét sírkő esetében működik, de én inkább informálisan Schelling-pontokban gondolkodom: vagyis olyan helyekben, amelyek olyan okokból tűnnek ki különlegesnek, amelyeket nem könnyű előre megjósolni.

Köszönet

Köszönöm mindenkinek, aki részt vett vagy retweetelte a szavazásomat, vagy megvitatta ezt velem a Twitteren

.