GeeksforGeeks

Előfeltétel – Gráfelmélet alapjai – 1. sorozat
A gráf olyan struktúra, amely olyan objektumok halmazából áll, amelyben az objektumok egyes párjai bizonyos értelemben “kapcsolatban állnak”. A gráf objektumainak a csúcsok, a köztük lévő kapcsolatoknak pedig az élek felelnek meg. A gráfot diagrammatikusan a csúcsokat ábrázoló pontok halmazaként ábrázoljuk, amelyeket éleket ábrázoló vonalak vagy görbék kötnek össze.
Formálisan,

“A gráf , a csúcsok (vagy csomópontok) nem üres halmazából és , az élek halmazából áll. Minden élhez egy vagy két csúcs tartozik, amelyeket végpontoknak nevezünk.”

A gráfok típusai :A gráfoknak több típusa van, amelyeket az élek, azok iránya, súlya stb. alapján különböztetünk meg.

1. Egyszerű gráf – Egyszerű gráfnak nevezzük azt a gráfot, amelyben minden él két különböző csúcsot köt össze, és ahol nincs két olyan él, amely ugyanazt a csúcspárt köti össze. Vegyük például a következő gráfot –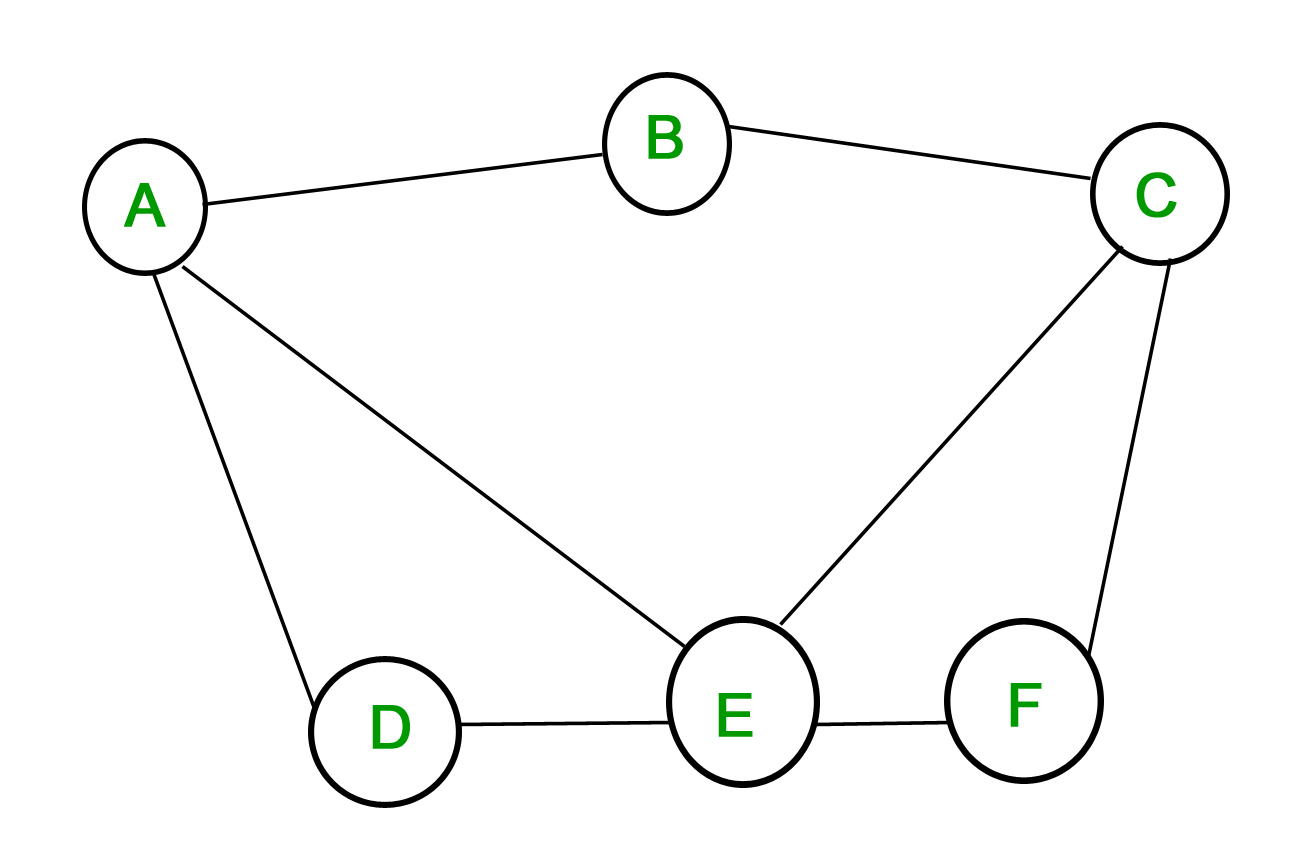

A fenti gráf egyszerű gráf, mivel egyetlen csúcsnak sincs önhurokja, és egyetlen két csúcsot sem köt össze egynél több él.
Az éleket az általuk összekötött csúcsokkal jelöljük- az az él, amely a és csúcsokat köti össze.

2. Multigráf – Az olyan gráfot, amelyben több él is összekötheti ugyanazt a csúcspárt, multigráfnak nevezzük.
Mivel ugyanazon csúcspár között több él is lehet, az él sokasága megadja a két csúcs közötti élek számát.

A fenti gráf multigráf, mivel és között több él is van. A él multiplicitása 2.

Néhány gráfban, ellentétben a fentiekkel, az élek irányítottak. Ez azt jelenti, hogy az objektumok közötti kapcsolat csak egyirányú és nem kétirányú. Az élek iránya bizonyos alkalmazásokban fontos lehet.

Az alapján, hogy az élek irányítottak-e vagy sem, lehetnek irányított és irányítatlan gráfok. Ez a tulajdonság kiterjeszthető egyszerű gráfokra és multigráfokra, így kaphatunk egyszerű irányított vagy irányítatlan egyszerű gráfokat és irányított vagy irányítatlan multigráfokat.

Az alapvető gráfterminológia :

A fenti értekezésben már elmagyaráztunk néhány, a gráfokra vonatkozó fogalmat, mint például csúcsok, élek, irányított és nem irányított élek stb. Vannak további kifejezések, amelyek a csúcsok és élek tulajdonságait írják le.

• Adjacencia – Egy gráfban két csúcs és szomszédosnak mondható, ha egy él végpontjai. Az él azt mondjuk, hogy a csúcsokkal incidens.
  Abban az esetben, ha az él irányított, szomszédosnak mondjuk -hoz, pedig -tól szomszédosnak. Itt azt mondjuk, hogy a kezdőcsúcs, pedig a végcsúcs.
• Fokozat – Egy csúcs fokozata a vele incidens élek száma, kivéve az önhurkot, amely kétszeresen járul hozzá a csúcs fokához. Egy csúcs fokát -vel jelöljük.
  Irányított gráfok esetén a fokot tovább osztályozzuk befelé és kifelé irányuló gráfokra. Egy csúcs in-degree-je azoknak az éleknek a száma, amelyeknek az adott csúcs a végpontja. Egy csúcs kimeneti fokozata azoknak az éleknek a száma, amelyeknek az adott csúcs a kezdőcsúcsa. A beléptetési fokot , a kimeneti fokot pedig jelöli.
  A városok közötti járatokat ábrázoló fenti irányított gráfban például a “Delhi” csomópont beléptetési foka 3, a kimeneti foka pedig szintén 3.

Megjegyzés: Ha egy csomópont foka nulla, akkor izoláltnak nevezzük. Ha a foka egy, akkor függőnek nevezzük.

Kézrázó tétel :

Mit kapnánk, ha egy gráf összes csúcsának fokozatait összeadnánk. Irányítatlan gráf esetén minden él kétszer járul hozzá, egyszer a kezdőcsúcsához, másodszor a végcsúcsához. Tehát a fokok összege egyenlő az élek számának kétszeresével. Ezt a tényt a Handshaking-tétel mondja ki.

Let  be an undirected graph with  edges. ThenIn case G is a directed graph,

A Handshaking-tételnek irányítatlan gráfok esetén van egy érdekes eredménye –

An undirected graph has an even number of vertices of odd degree.

Bizonyítás : Legyen és a páros, illetve páratlan fokú csúcsok halmaza.
A kézfogási tételből tudjuk, hogy,

Így,

a páros fokú csúcsok fokainak összege páros. Az LHS is páros, ami azt jelenti, hogy a páratlan fokú csúcsok fokainak összege is páros kell, hogy legyen.
Ezért a páratlan fokú csúcsok száma páros.

Néhány speciális egyszerű gráf :

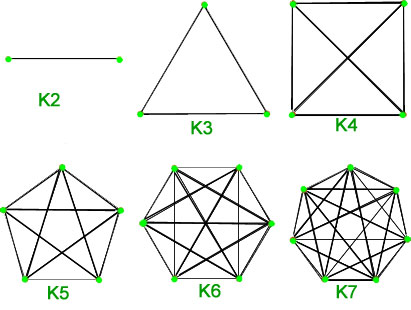
1. Teljes gráfok – Az csúcsokból álló olyan egyszerű gráfot, amelynek minden csúcspár között pontosan egy él van, teljes gráfnak nevezzük. Az csúcsból álló teljes gráfot -vel jelöljük. A teljes gráfban az élek száma n*(n-1)/2, n csúccsal.

2. Ciklusok – A ciklusok olyan egyszerű gráfok, amelyek csúcsai , élei . A csúccsal rendelkező ciklust -vel jelöljük. Az élek száma összesen n, n csúccsal a ciklusgráfban.

3. Kerék – A kerék ugyanolyan, mint a ciklus, egy további csúccsal, amely minden más csúcshoz kapcsolódik. Az csúcsokból álló kerekeket, amelyekben 1 további csúcs van, jelöljük. Az élek száma összesen 2*(n-1) n csúccsal a kerékgráfban.

4. Hiperkocka – A hiperkocka vagy n-kocka egy olyan gráf, amelynek csúcsait egy-egy n bites karakterlánc jelöli. A legfeljebb 1 bittel különböző csúcsokat élek kötik össze. Egy csúcsból álló hiperkockát a jelöli. Az élek száma összesen n*, a kocka gráfjában csúcsok vannak.

5. Kétrészes gráfok – Egy egyszerű gráfot kétrészesnek mondunk, ha a csúcshalmaza két diszjunkt halmazra osztható úgy, hogy minden élének kezdőcsúcsa az első halmazban, végcsúcsa pedig a második halmazban van. A bipartit gráfban az élek száma összesen (n*m), (n+m) csúccsal.

Tétel – Egy egyszerű gráf akkor és csak akkor bipartit, ha a gráf minden egyes csúcsához két
különböző szín közül egyet lehet rendelni úgy, hogy két szomszédos csúcsnak ne legyen
egyforma színe.

Egy kétrészes gráfot, amelynek két diszjunkt részhalmazában és csúcs van, teljesnek mondjuk, ha az első halmaz minden csúcsából van egy él a második halmaz minden csúcsába, összesen él. Egy teljes kétrészes gráfot, amelynek csúcsa van az első halmazban és csúcsa a második halmazban, -nek nevezzük.

GATE CS Corner Questions

Az alábbi kérdések gyakorlásával tesztelheti tudását. Minden kérdést a GATE korábbi években vagy a GATE próbavizsgákon tettek fel. Nagyon ajánlott gyakorolni őket.

1. GATE CS 2013, 25. kérdés
2. GATE CS 2014 Set-1, 61. kérdés
3. GATE CS 2006, 71. kérdés
4. GATE CS 2002, 25. kérdés
5. GATE CS 2004, 37. kérdés
6. GATE CS 2014 Set-2, 13. kérdés

Hivatkozások-

Graphs – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen

Ezzel a szócikkel Chirag Manwani foglalkozik. Ha tetszik a GeeksforGeeks és szeretnél hozzájárulni, írhatsz cikket a contribute.geeksforgeeks.org címen, vagy elküldheted a cikkedet a [email protected] címre. Láthatod, hogy a cikked megjelenik a GeeksforGeeks főoldalán, és segíthetsz más geekeknek.