- Az összekapcsolhatóság a gráfelmélet egyik alapfogalma. Meghatározza, hogy egy gráf összefüggő vagy összefüggéstelen. Összekapcsolhatóság nélkül nem lehet egy gráfot egyik csúcsból a másik csúcsba átjárni.
- Egy gráfot összekapcsolt gráfnak nevezünk, ha minden csúcspár között van egy út. Minden csúcsból bármelyik másik csúcsba kell, hogy legyen valamilyen útvonal, amelyen át lehet haladni. Ezt nevezzük a gráf összekapcsolhatóságának.
- Egy gráfot összekapcsolatlannak mondjuk, ha több összekapcsolatlan csúcs és él is létezik.
- A gráf összekapcsolhatósági elméletei alapvető fontosságúak a hálózati alkalmazásokban, a közlekedési hálózatok útvonalvezetésében, a hálózati toleranciában stb.
Példa
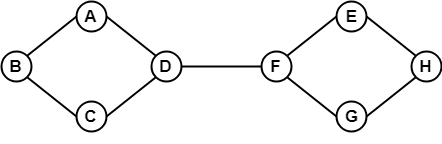
A fenti példában az egyik csúcsból a másik csúcsba lehet utazni. Itt a B csúcstól H-ig a B -> A -> D -> F -> E -> H útvonalon tudunk átmenni.
Példa
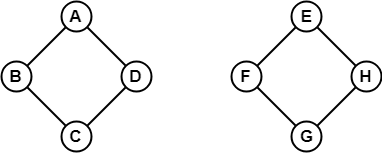
A fenti példában a B csúcstól H-ig nem lehet átmenni, mert sem közvetlenül, sem közvetve nincs út köztük. Ezért ez egy összefüggéstelen gráf.
Lássunk néhány alapfogalmat az összekapcsolhatóságról.
Vágott csúcs
Az egyetlen csúcsot, amelynek eltávolítása egy gráfot szétkapcsol, vágott csúcsnak nevezzük.
Legyen G egy összefüggő gráf. G egy v csúcsát G vágott csúcsának nevezzük, ha G-v (Remove v from G) egy összekapcsolt gráfot eredményez.
Ha egy gráfból eltávolítunk egy csúcsot, akkor a gráf két vagy több gráfra szakad. Ezt a csúcsot vágott csúcsnak nevezzük.
Megjegyzés: Legyen G egy n csúcsú gráf:
- Egy összefüggő G gráfnak legfeljebb (n-2) vágott csúcsa lehet.
- Egy vágott csúcs eltávolításával a gráf szétkapcsolatlan maradhat.
- Egy csúcs eltávolítása legalább eggyel növelheti a gráf összetevőinek számát.
- Egy fa minden nem függő csúcsa vágott csúcs.
Példa 1

Példa 2
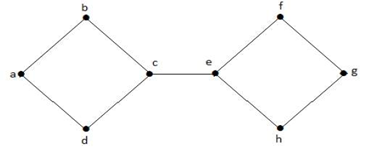
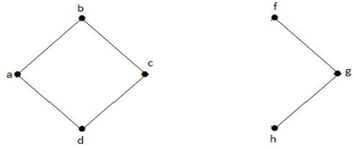
A fenti gráfban az ‘e’ csúcs vágott csúcs. Miután eltávolítottuk az ‘e’ csúcsot a fenti gráfból, a gráf összefüggéstelen gráffá válik.
Vágott él (híd)
A vágott él vagy híd olyan egyetlen él, amelynek eltávolítása szétkapcsolja a gráfot.
Legyen G egy összefüggő gráf. G egy e élét G vágott élének nevezzük, ha G-e (E eltávolítása G-ből) egy összefüggéstelen gráfot eredményez.
Ha eltávolítunk egy élt egy gráfból, akkor a gráf két vagy több gráfra szakad. Ezt az eltávolított élt vágott élnek vagy hídnak nevezzük.
Megjegyzés: Legyen G egy n csúcsú gráf:
- Egy összefüggő G gráfnak legfeljebb (n-1) vágott éle lehet.
- Egy vágott él eltávolításával a gráf szétkapcsolatlan maradhat.
- Egy él eltávolítása legfeljebb eggyel növelheti a gráf összetevőinek számát.
- Egy “e” vágott él nem lehet része G egyetlen ciklusának sem.
- Ha létezik vágott él, akkor léteznie kell vágott csúcsnak is, mert a vágott élnek legalább egy csúcsa vágott csúcs.
- Ha létezik vágott csúcs, akkor nem szükséges bármely vágott él létezése.
1. példa
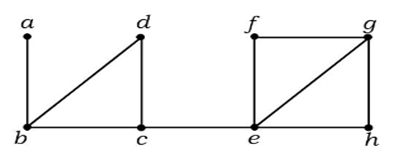
A fenti gráfban a (c, e) él egy vágott él. Miután eltávolítottuk ezt az élt a fenti gráfból, a gráf összefüggéstelen gráf lesz.
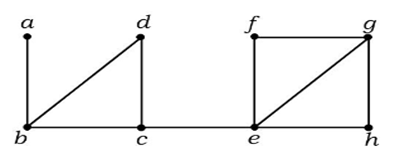
2. példa
A fenti gráfban a (c, e) él egy vágott él. Miután eltávolítottuk ezt az élt a fenti gráfból, a gráf összefüggéstelen gráffá válik.
Vágott halmaz
Egy G összefüggő gráfban a vágott halmaz az élek S halmaza, amely a következő tulajdonságokkal rendelkezik:
- Az S-ben lévő összes él eltávolítása G-t összefüggéstelenné teszi.
- Az S néhány élének (de nem az összesnek) az eltávolítása nem szakítja meg G-t.
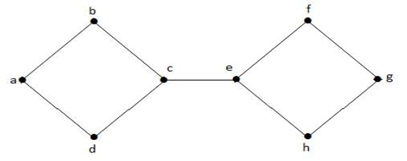
1. példa
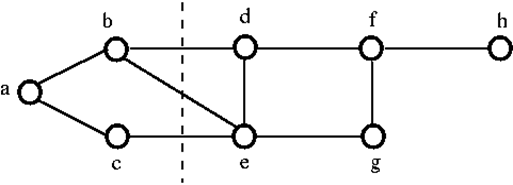
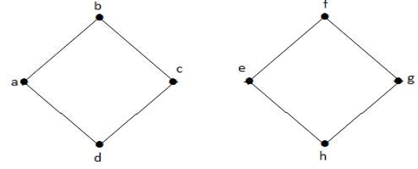
A fenti G gráf szétkapcsolásához el kell távolítanunk a három élt, azaz a bd, be és ce éleket. A három élből csak kettőt eltávolítva nem tudjuk szétkapcsolni. Ezért {bd, be, ce} egy vágott halmaz.
A vágott halmaz eltávolítása után a fenti gráf a következőképpen néz ki:
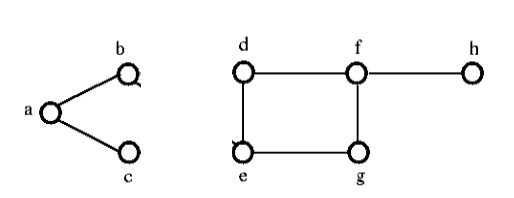
Élek összekapcsolhatósága
A G összefüggő gráf élkapcsolhatósága azon élek minimális száma, amelyek eltávolítása miatt G nem kapcsolódik. Ezt λ(G) jelöli.
Ha λ(G) ≥ k, akkor G gráfot k éllel összefüggőnek mondjuk.
Példa
Lássunk egy példát,
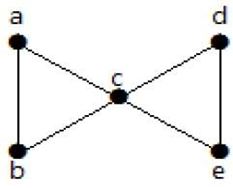
A fenti gráfból két minimális él eltávolításával az összefüggő gráf összefüggéstelen gráffá válik. Tehát az élkapcsolhatósága 2. Ezért a fenti gráf egy 2-élű összekapcsolt gráf.
Itt van a következő négy módja annak, hogy a gráfot két él eltávolításával szétkapcsoljuk:
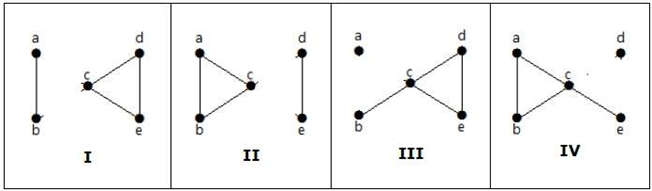
Szegélykapcsolhatóság
A G összefüggő gráf kapcsolhatósága (vagy csúcskapcsolhatósága) azon csúcsok minimális száma, amelyek eltávolításával G szétkapcsolódik vagy triviális gráffá redukálódik. Ezt K(G)-vel jelöljük.
A gráfot akkor mondjuk k-összekötöttnek vagy k-csúcsösszekötöttnek, ha K(G) ≥ k. Egy csúcs eltávolításához a rá eső éleket is el kell távolítanunk.
Példa
Lássunk egy példát:
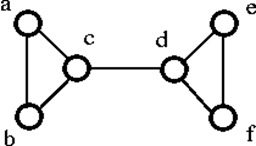
A fenti G gráf a ‘c’ vagy ‘d’ egyetlen csúcsának eltávolításával szétkapcsolható. Ezért a csúcsok összekapcsolhatósága 1. Ezért ez egy 1 összekapcsolt gráf.