Az irányított aciklikus gráf topológiai rendezése

Bevezetés

A számítástechnikában az irányított aciklikus gráf (DAG) olyan irányított gráf, amelyben nincsenek ciklusok. Ebben a bemutatóban megmutatjuk, hogyan lehet topológiai rendezést végezni egy DAG-on lineáris idő alatt.

Topológiai rendezés

Sok alkalmazásban használunk irányított aciklikus gráfokat az események közötti precedenciák jelölésére. Például egy ütemezési problémában van egy feladathalmaz és egy, a feladatok sorrendjét meghatározó kényszerhalmaz. A feladatok ábrázolására egy DAG-ot konstruálhatunk. A DAG irányított élei a feladatok sorrendjét reprezentálják.

Lássunk egy olyan problémát, hogy egy személy hogyan öltözik fel egy hivatalos alkalomra. Több ruhadarabot kell felvennünk, például zoknit, nadrágot, cipőt stb. Néhány ruhadarabot előbb kell felvenni, mint a többit. Például a zoknit a cipő előtt kell felvennünk. Néhány ruhadarabot bármilyen sorrendben felvehetünk, például a zoknit és a nadrágot. Egy DAG segítségével szemléltethetjük ezt a problémát:

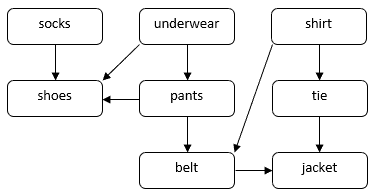
Ebben a DAG-ban a csúcsok ruhadaraboknak felelnek meg. A DAG-ban egy közvetlen él jelzi, hogy a ruhadarabot a ruhadarab előtt kell felvennünk. A feladatunk az, hogy a függőségi megkötések betartása mellett megtaláljuk az összes ruhadarab felöltésének sorrendjét. Például a ruhadarabokat a következő sorrendben vehetjük fel:

A DAG topológiai rendje az összes csúcsának olyan lineáris rendezése, hogy ha tartalmaz egy élt, akkor a rendezésben előtt szerepel. Egy DAG-ra olyan topológiai rendezést állíthatunk elő, amelynek futási ideje lineáris a csúcsok számával és az élek számával, ami .

Kahn algoritmus

Egy DAG-ban minden két csúcs közötti út véges hosszúságú, mivel a gráf nem tartalmaz ciklust. Legyen a leghosszabb út (forráscsúcs) és (célcsúcs) között. Mivel a leghosszabb út, nem lehet bejövő él -be. Ezért a DAG legalább egy olyan csúcsot tartalmaz, amelynek nincs bejövő éle.

3.1. Kahn algoritmusa

A Kahn algoritmusban egy DAG topológiai rendezését úgy állítjuk össze, hogy olyan csúcsokat találunk, amelyeknek nincs bejövő éle:

Ezzel az algoritmussal először kiszámítjuk az összes csúcs beléptetési fokának értékét.

Ezt követően egy olyan csúccsal kezdünk, amelynek beléptetési foka 0, és a kimeneti lista végére tesszük. Miután kiválasztottunk egy csúcsot, frissítjük a szomszédos csúcsok in-degree értékeit, mert a csúcsot és a kimenő éleit eltávolítjuk a gráfból.

A fenti folyamatot addig ismételjük, amíg az összes csúcsot ki nem választjuk. A kimeneti lista ekkor a gráf topológiai rendezése.

3.2. A gráf topológiai rendezése. Időbonyolultság

Hogy kiszámítsuk az összes csúcs belsejében lévő fokokat, meg kell látogatnunk a összes csúcsát és élét. Ezért a futási idő a fokon belüli számításokhoz. Hogy elkerüljük ezeknek az értékeknek az újbóli kiszámítását, használhatunk egy tömböt, hogy nyomon kövessük ezeknek a csúcsoknak a fokon belüli értékeit. A while cikluson belül is meg kell látogatnunk az összes csúcsot és élt. Ezért a teljes futási idő .

Mélységi első keresés

A topológiai rendezés felépítéséhez használhatunk mélységi első keresési (DFS) algoritmust is.

4.1. A topológiai rendezés felépítése

. Gráf DFS rekurzióval

Mielőtt a topológiai rendezés aspektusával foglalkoznánk a DFS segítségével, kezdjük egy standard, rekurzív gráf DFS átjárási algoritmusának áttekintésével:

A standard DFS algoritmusban a egy véletlenszerű csúcsával kezdünk, és ezt a csúcsot látogatottnak jelöljük. Ezután rekurzívan meghívjuk a dfsRecursive függvényt, hogy meglátogassuk az összes nem látogatott szomszédos csúcsot. Ily módon idő alatt meglátogathatjuk a összes csúcsát.

Mivel azonban minden csúcsot azonnal a listába teszünk, amikor meglátogatjuk, és mivel bármelyik csúcson kezdhetjük, a standard DFS algoritmus nem garantálja, hogy topológiailag rendezett listát hoz létre.

Nézzük meg, mit kell tennünk, hogy ezt a hiányosságot kiküszöböljük.

4.2. A DFS algoritmus a DFS algoritmussal a listába helyezi a csúcsokat. DFS alapú topológiai rendezési algoritmus

Módosíthatjuk a DFS algoritmust, hogy egy DAG topológiai rendezését generálja. A DFS átjárás során, miután egy csúcs minden szomszédját meglátogattuk, az eredménylista elejére helyezzük. Így biztosíthatjuk, hogy az összes szomszédja előtt jelenjen meg a rendezett listában:

Ez az algoritmus hasonló a standard DFS algoritmushoz. Bár továbbra is egy véletlenszerű csúccsal kezdünk, de nem tesszük be a listába azonnal, amint meglátogatjuk a csúcsot. Ehelyett először rekurzívan meglátogatjuk az összes szomszédját, majd a csúcsot a lista elejére tesszük. Ezért, ha tartalmaz egy élt, akkor a előtt jelenik meg a listában.

A teljes futási idő is , mivel ugyanolyan időbonyolultságú, mint a DFS algoritmus.

Következtetés

A cikkben bemutattunk egy példát a topológiai rendezésre egy DAG-on. Továbbá tárgyaltunk két olyan algoritmust, amelyekkel idő alatt lehet topológiai rendezést végezni.

A DFS alapú topológiai rendezési algoritmus Java implementációja elérhető a Depth First Search in Java című cikkünkben.