Amikor a modell előrejelzéséről beszélünk, fontos megérteni az előrejelzési hibákat (torzítás és variancia). Van egy kompromisszum a modell azon képessége között, hogy minimalizálja a torzítást és a szórást. Ezeknek a hibáknak a megfelelő megértése nem csak abban segít, hogy pontos modelleket építsünk, hanem abban is, hogy elkerüljük a túlillesztés és az alulillesztés hibáját.
Kezdjük tehát az alapokkal, és nézzük meg, milyen különbséget jelentenek a gépi tanulási modelljeinkben.
Mi a torzítás?
A torzítás a különbség a modellünk átlagos előrejelzése és a helyes érték között, amelyet megpróbálunk megjósolni. A nagy torzítással rendelkező modell nagyon kevés figyelmet fordít a képzési adatokra, és túlzottan leegyszerűsíti a modellt. Ez mindig magas hibához vezet a képzési és tesztadatokon.
Mi a variancia?
A variancia a modell előrejelzésének változékonysága egy adott adatpontra vagy egy értékre, amely az adataink szórásáról árulkodik. A nagy varianciával rendelkező modell nagy figyelmet fordít a képzési adatokra, és nem általánosít azokra az adatokra, amelyeket még nem látott. Ennek eredményeképpen az ilyen modellek nagyon jól teljesítenek a képzési adatokon, de a tesztadatokon magas hibaszázalékkal rendelkeznek.
Matematikusan
Legyen a változó, amelyet megpróbálunk megjósolni, Y, a többi kovariáns pedig X. Feltételezzük, hogy a kettő között olyan kapcsolat van, hogy
Y=f(X) + e
amelyben e a hibaterminus, és normális eloszlású, átlaga 0.
Lineráris regresszióval vagy bármely más modellezési technikával f^(X) modellt készítünk f(X)-ből.
Az x pontnál várható négyzetes hiba tehát
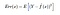
a Err(x) tovább bontható

Err(x) a Bias² összege, szórás és a redukálhatatlan hiba összege.
A redukálható hiba az a hiba, amelyet nem lehet jó modellek készítésével csökkenteni. Ez az adatainkban lévő zaj mértékegysége. Itt fontos megérteni, hogy bármennyire is jó modellt készítünk, adatainkban lesz bizonyos mennyiségű zaj vagy irreducibilis hiba, amelyet nem lehet eltávolítani.
Bias és variancia a bikaszem diagram segítségével

A fenti diagramban a célpont közepén egy olyan modell áll, amely tökéletesen jósolja a helyes értékeket. Ahogy távolodunk a céltáblától, előrejelzéseink egyre rosszabbak lesznek. Megismételhetjük a modellépítés folyamatát, hogy külön találatokat kapjunk a célpontra.
A felügyelt tanulásban az alulilleszkedés akkor fordul elő, amikor a modell nem képes megragadni az adatok mögöttes mintázatát. Ezek a modellek általában nagy torzítással és alacsony szórással rendelkeznek. Ez akkor fordul elő, amikor nagyon kevés adatunk van egy pontos modell felépítéséhez, vagy amikor nemlineáris adatokkal próbálunk lineáris modellt építeni. Emellett az ilyen típusú modellek nagyon egyszerűek az adatok összetett mintázatainak megragadására, mint például a lineáris és a logisztikus regresszió.
A felügyelt tanulásban a túlillesztés akkor következik be, amikor a modellünk az adatok mögöttes mintázatával együtt a zajt is megragadja. Ez akkor történik, amikor a modellünket sokat képezzük zajos adathalmazon. Ezek a modellek alacsony torzítással és magas szórással rendelkeznek. Ezek a modellek nagyon összetettek, mint például a döntési fák, amelyek hajlamosak a túlillesztésre.

Miért van torzítás-variáció tradeoff?
Ha a modellünk túl egyszerű és nagyon kevés paraméterrel rendelkezik, akkor magas lehet a torzítás és alacsony a variancia. Másrészt, ha a modellünknek nagyszámú paramétere van, akkor magas szórással és alacsony torzítással fog rendelkezni. Tehát meg kell találnunk a megfelelő/jó egyensúlyt anélkül, hogy túlillesztjük vagy alulillesztjük az adatokat.
A komplexitásnak ez a kompromisszuma az oka annak, hogy a torzítás és a variancia között kompromisszum van. Egy algoritmus nem lehet egyszerre bonyolultabb és kevésbé bonyolult.
Teljes hiba
A jó modell megalkotásához meg kell találnunk a jó egyensúlyt a torzítás és a variancia között úgy, hogy az minimalizálja a teljes hibát.

A torzítás és a szórás optimális egyensúlya soha nem alkalmazza túl vagy alul a modellt.
Ezért a torzítás és a variancia megértése kritikus fontosságú az előrejelző modellek viselkedésének megértéséhez.
Köszönjük az olvasást!