 Kady Dupre
Kady Dupre
Itt egy szófeladat neked:
Péntek kisasszony osztálya naponta megold egy szófeladatot. Tíz diákja remekül oldja meg az összeadással kapcsolatos szófeladatokat, és csak hét diákja tűnik úgy, hogy érti a kivonással kapcsolatos szófeladatokat. Öt diákja unja a könnyű feladatokat. Tizenhárom tanuló még mindig küszködik az alapvető matematikai tényekkel, 3-nak pedig egyáltalán nem megy a szófeladatok elolvasása. Hány tanulója elkötelezett és tanul?
Itt egy jobb kérdés: “
Miért küzdenek a diákok a matematikai szöveges feladatokkal
A diákok sokféle okból küzdenek a matematikai szöveges feladatokkal, de a három legnagyobb, amivel találkoztam, a következő:
1. probléma: A diákok önbizalma
Sok diák számára már a szöveges feladatok nézése is szorongáshoz vezet. Senki sem tud tisztán gondolkodni, ha rettegés vagy a kudarctól való félelem fenyeget!
Kérdés #2: Rugalmas gondolkodás
Sok gyereket arra tanítanak, hogy a szóproblémákat módszeresen, előírásos lépésről lépésre, kulcsszavak segítségével oldja meg, ami nem mindig működik. A tervek nagyszerűek, de nem akkor, ha a tanulók inkább mankóként, mint eszközként használják őket. A mai szabványosított tesztek és a valós alkalmazások kreatív gondolkodást és rugalmas stratégiákat igényelnek.
Harmadik kérdés: Differenciálás
A tanárok azt akarják, hogy a diákok gyorsan kiemelkedjenek, és gyakran túl gyorsan, túl hamar nyomulnak. A szöveges feladatok esetében lassan kell haladni, hogy gyorsan haladhassunk. Akárcsak az irányított olvasásnál, itt is sok gyakorlatot kell adni az “éppen megfelelő” feladatokkal, és irányított gyakorlást kell biztosítani a tanulók szintje fölötti feladatokkal.”
3 problémamegoldó stratégia
A megoldás a matematikai szóproblémák meghódítása a fenti problémákat ellensúlyozó, magával ragadó tantermi stratégiákkal!
1. Tanítson problémamegoldó rutint
A gyerekek (és a felnőttek) köztudottan impulzív problémamegoldók. Sok diák meglát egy szöveges feladatot, és azonnal ki akarja ragadni azokat a számokat, hogy “csináljon velük valamit”. Amikor én általános iskolába jártam, ez tulajdonképpen elég megbízható stratégia volt! Manapság azonban a gyerekeknek sokkal összetettebb feladatokat kell megoldaniuk, gyakran trükkös megfogalmazásokkal vagy szándékos zavaró tényezőkkel.
Rutin tanításával rugalmas gondolkodókat nevelhetsz és önbizalmat építhetsz. A problémamegoldási rutin egyszerűen arra ösztönzi a tanulókat, hogy lassítsanak és gondolkodjanak a megoldás előtt és után. Sok hatékony rutint láttam már, de a kedvenceim mindig tartalmazzák az “előtte, közben és utána” gondolkodásmódot.
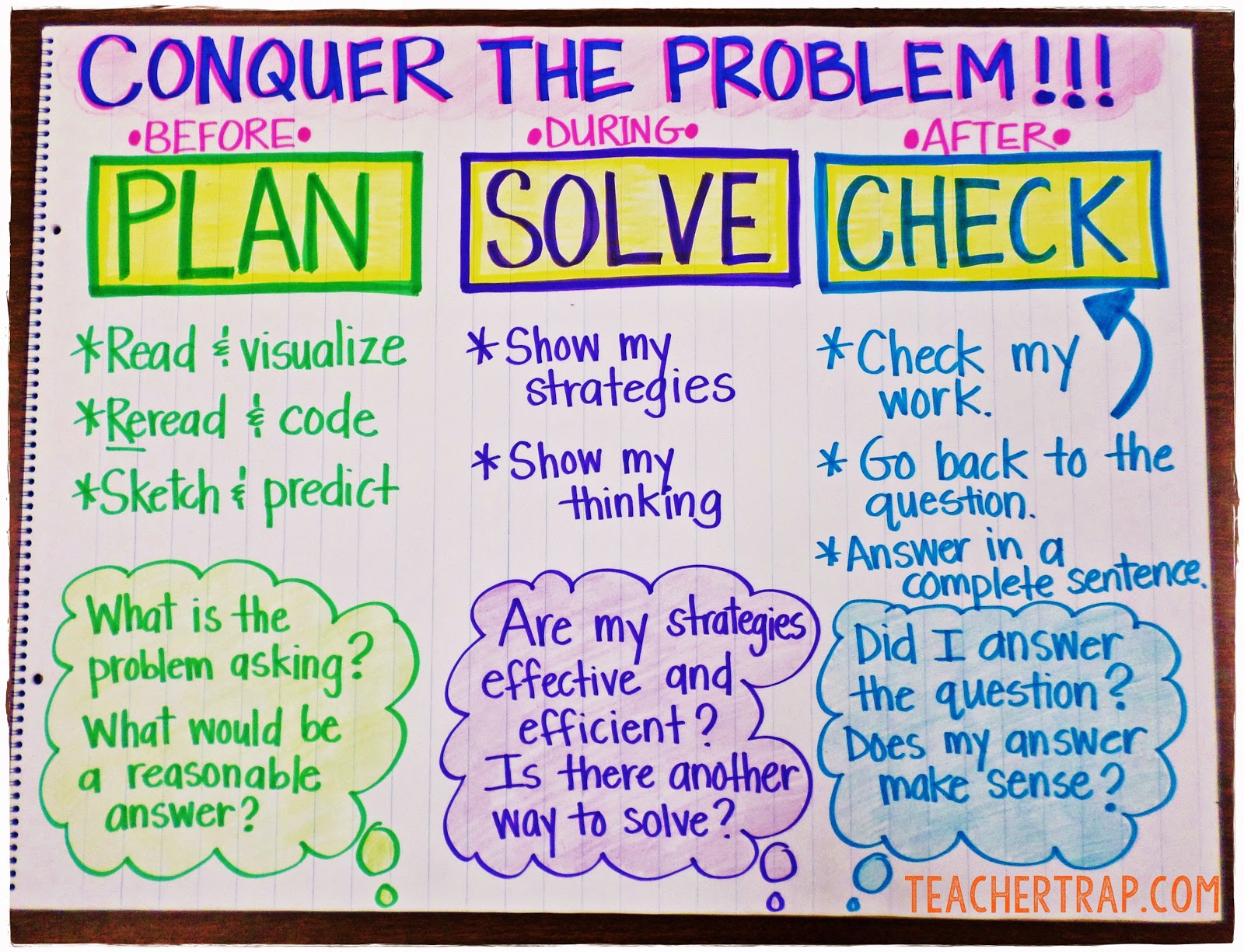
Hogy a problémamegoldási rutin értelmes és hatékony legyen:
- Használja gyakran (lehetőleg naponta)
- Beépíti a “Turn & Teach” (A diákok szóban elmagyarázzák gondolkodásukat és folyamatukat egy társuknak.)
Megengedi a “stratégia megosztását” a megoldás után (A kiválasztott tanulók elmagyarázzák módszerüket és gondolkodásukat.)

2. Differenciálja a szófeladatokat
Nem, ez nem azt jelenti, hogy minden tanulónak más szófeladatot írjunk! Ez lehet olyan egyszerű, mint a számok kiigazítása egy feladatban vagy a zavaró tényezők eltávolítása a nehézségekkel küzdő tanulók számára. A szóproblémák állványozása növeli a magabiztosságot és javítja a problémamegoldó készséget azáltal, hogy fokozatosan növeli a szint nehézségét, ahogy a gyermek készen áll rá. Ez különösen akkor hatékony, ha a tanulóknak különböző szerkezetű szóproblémákat próbálsz megtanítani egy adott művelethez.
Az összehasonlító kivonási feladatok például nagy kihívást jelentenek egyes tanulók számára. Ha egy egyszerű változattal kezdjük, lehetővé tesszük a tanulók számára, hogy magára a problémára koncentráljanak, ahelyett, hogy megfélemlítenék vagy frusztrálnák őket.

Az irányított matematikai csoportjaimnál nagy sikert értem el az állványozott feladatok használatával. Miután megoldották a könnyebb feladatot, a tanulók rájönnek, hogy az nem is olyan bonyolult, és készen állnak a nehezebbek megoldására!
3. Hasonlítsuk össze a feladatokat egymás mellett
A rugalmas gondolkodás fejlesztéséhez nincs hatásosabb, mint a szöveges feladatok elemzése és összehasonlítása. Kezdjük olyan feladatokkal, amelyek hasonló történettel és számokkal, de eltérő problémaszerkezettel rendelkeznek. Bátorítsuk a beszélgetést, használjunk vizuális ábrázolásokat, és a tanulókkal magyaráztassuk el a szerkezet és a műveletek közötti különbséget. Íme egy példa, amely a tanulók munkáját mutatja két hasonló, majmokról szóló feladattal kapcsolatban. Kattintson ide, ha le szeretné tölteni e problémák üres példányát. A freebie-m több variációt is tartalmaz a differenciáláshoz.

Használd ezt a három stratégiát, hogy a gyerekek elgondolkodjanak és beszélgessenek a problémamegoldási stratégiáikról, miközben kialakul az “oly fontos” önbizalom, és máris meghódíthatod a matematikai szóproblémákat!
