Oppimistulokset

  • Määritä kuvaavatko tiedot tai skenaario lineaarista vai geometrista kasvua
  • Tunnista kasvuvauhti, alkuarvot tai pistearvot sanallisesti ja graafisesti, tai numeerisesti, ja muuntaa ne laskennallisesti käyttökelpoiseen muotoon
  • Laskemaan rekursiivisia ja eksplisiittisiä yhtälöitä lineaariselle ja geometriselle kasvulle, kun käytettävissä on riittävästi tietoa, ja käyttämään näitä yhtälöitä ennusteiden tekemiseen

Lineaarisen kasvun ominaispiirre on vakio muutosnopeus. Vakiomuutokseen liittyvien koordinaattiparien piirtäminen antaa tulokseksi suoran viivan, joka on lineaarisen kasvun muoto. Tässä jaksossa muodollistetaan tapa kuvata lineaarista kasvua matemaattisten termien ja käsitteiden avulla. Tämän jakson lopussa osaat kirjoittaa sekä rekursiivisen että eksplisiittisen yhtälön lineaariselle kasvulle, kun lähtöolosuhteet tai muutosvakio on annettu. Osaat myös tunnistaa lineaarisen ja geometrisen kasvun välisen eron kuvaajan tai yhtälön perusteella.

Lineaarinen (algebrallinen) kasvu

Kasvun ennustaminen

Marco on antiikkisten limsapullojen keräilijä. Hänen kokoelmassaan on tällä hetkellä 437 pulloa. Joka vuosi hän budjetoi tarpeeksi rahaa ostaakseen 32 uutta pulloa. Voimmeko määrittää, kuinka monta pulloa hänellä on 5 vuoden kuluttua ja kuinka kauan kestää, ennen kuin hänen kokoelmansa saavuttaa 1000 pulloa?

Vaikka voisit luultavasti ratkaista molemmat näistä kysymyksistä ilman yhtälöä tai muodollista matematiikkaa, aiomme virallistaa lähestymistapamme tähän ongelmaan, jotta voimme vastata monimutkaisempiin kysymyksiin.

Esitämme, että Pn edustaa pullojen lukumäärää tai populaatiota, joka Marcon kokoelmalla on n:n vuoden kuluttua. P0 edustaisi siis pullojen lukumäärää nyt, P1 edustaisi pullojen lukumäärää vuoden kuluttua, P2 edustaisi pullojen lukumäärää kahden vuoden kuluttua ja niin edelleen. Voisimme kuvata, miten Marcon pullokokoelma muuttuu käyttämällä:

P0 = 437

Pn = Pn-1 + 32

Tätä kutsutaan rekursiiviseksi suhteeksi. Rekursiivinen suhde on kaava, joka liittää sarjan seuraavan arvon edellisiin arvoihin. Tässä tapauksessa pullojen lukumäärä vuonna n saadaan lisäämällä 32 edellisen vuoden pullojen lukumäärään Pn-1. Tämän suhteen avulla voimme laskea:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Olemme vastanneet kysymykseen, montako pulloa Marcolla on viiden vuoden kuluttua.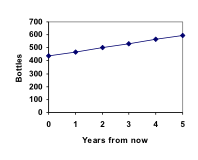

Mutta sen ratkaiseminen, kuinka kauan kestää, että hänen kokoelmansa saavuttaa 1000 pulloa, vaatisi paljon enemmän laskutoimituksia.

Kun rekursiiviset suhteet ovatkin erinomaisia, kun halutaan kuvata yksinkertaisesti ja siististi, miten jokin suure muuttuu, ne eivät ole käteviä, kun halutaan tehdä ennusteita tai ratkaista pitkälle tulevaisuuteen ulottuvia ongelmia. Sitä varten suositellaan suljettua tai eksplisiittistä muotoa suhteelle. Selkeän yhtälön avulla voimme laskea Pn suoraan ilman, että meidän tarvitsee tietää Pn-1. Vaikka voit ehkä jo arvata eksplisiittisen yhtälön, johdetaan se rekursiivisesta kaavasta. Voimme tehdä sen jättämällä valikoivasti yksinkertaistamatta mennessämme:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Voit varmaan nyt nähdä kaavan ja yleistää, että

Pn = 437 + n(32) = 437 + 32n

Tämän yhtälön avulla voimme laskea, kuinka monta pulloa hänellä on 5 vuoden kuluttua:

P5 = 437 + 32(5) = 437 + 160 = 597

Voidaan nyt myös ratkaista, milloin kokoelma saavuttaa 1000 pulloa, korvaamalla Pn:n arvolla 1000 ja ratkaisemalla n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Siten Marco saavuttaa 1000 pulloa 18 vuodessa.

Vaiheet kaavan määrittämiseksi ja Marcon pullokokoelman ongelman ratkaisemiseksi on selitetty yksityiskohtaisesti seuraavissa videoissa.

Tässä esimerkissä Marcon kokoelma kasvoi joka vuosi saman määrän pulloja. Tämä jatkuva muutos on lineaarisen kasvun tunnusmerkki. Kun piirrämme Marcon kokoelmalle laskemamme arvot, voimme nähdä, että arvot muodostavat suoran viivan, joka on lineaarisen kasvun muoto.

Lineaarinen kasvu

Jos määrä alkaa koosta P0 ja kasvaa d:llä jokaisella aikajaksolla, määrä n aikajakson jälkeen voidaan määrittää jommankumman näistä suhteista avulla:

Rekursiivinen muoto

Pn = Pn-1 + d

Explisiittinen muoto

Pn = P0 + d n

Tässä yhtälössä d edustaa yhteistä eroa – määrää, jonka populaatio muuttuu joka kerta, kun n kasvaa yhdellä.

Yhteys aikaisempaan oppimiseen: Slope and Intercept

Olet ehkä tunnistanut lineaarisen yhtälömme yhteisen erotuksen, d, kaltevuudeksi. Itse asiassa koko eksplisiittisen yhtälön pitäisi näyttää tutulta – se on sama lineaarinen yhtälö, jonka olet oppinut algebrassa ja joka on luultavasti esitetty muodossa y = mx + b.

Vakiomuotoisessa algebrallisessa yhtälössä y = mx + b b oli y:n leikkauspiste eli y:n arvo, kun x oli nolla. Käyttämässämme yhtälömuodossa käytämme P0:ta kuvaamaan tuota alkusummaa.

Yhtälössä y = mx + b muistetaan, että m oli kaltevuus. Saatat muistaa sen ”nousuna yli juoksun” tai y:n muutoksena jaettuna x:n muutoksella. Oli miten oli, se edustaa samaa asiaa kuin käyttämämme yhteinen erotus d – sitä määrää, jonka ulostulo Pn muuttuu, kun sisääntulo n kasvaa 1:llä.

Yhtälöt y = mx + b ja Pn = P0 + d n tarkoittavat samaa asiaa, ja niitä voidaan käyttää samoin tavoin. Kirjoitamme ne vain hieman eri tavalla.

Esimerkkejä

Kansallisen metsän hirvikanta mitattiin 12 000:ksi vuonna 2003, ja se mitattiin uudelleen 15 000:ksi vuonna 2007. Jos populaatio jatkaa lineaarista kasvua tällä vauhdilla, mikä on hirvikanta vuonna 2014?

Näytä ratkaisu

Aluksi meidän on määriteltävä, miten aiomme mitata n. Muistakaa, että P0 on populaatio, kun n = 0, joten emme luultavasti halua käyttää kirjaimellisesti vuotta 0. Koska tiedämme jo vuoden 2003 väkiluvun, määrittelemme n = 0:ksi vuoden 2003.

Tällöin P0 = 12 000.

Seuraavaksi meidän on löydettävä d. Muistakaa, että d on kasvu ajanjaksoa kohti, tässä tapauksessa kasvu vuotta kohti. Kahden mittauksen välillä väestö kasvoi 15 000-12 000 = 3 000, mutta kesti 2007-2003 = 4 vuotta kasvaa niin paljon. Saadaksemme kasvun vuotta kohti, voimme jakaa: 3000 hirveä / 4 vuotta = 750 hirveä vuodessa.

Vaihtoehtoisesti voit käyttää algebran kaltevuuskaavaa yhteisen erotuksen määrittämiseksi, huomioiden, että populaatio on kaavan ulostulo ja aika on tulo.

d=slope=\frac{\text{changeinoutput}}{\text{changeininput}}=\frac{15,000-12,000}{2007-2003}=\frac{3000}{4}=750

Voidaan nyt kirjoittaa yhtälömme haluamassamme muodossa.

Rekursiivinen muoto

P0 = 12 000

Pn = Pn-1 + 750

Explisiittinen muoto

Pn = 12 000 + 750(n)

Vastaaksemme kysymykseen, meidän on ensin huomioitava, että vuodeksi 2014 tulee n = 11, koska vuosi 2014 on 11 vuotta vuoden 2003 jälkeen. Eksplisiittistä muotoa on helpompi käyttää tähän laskutoimitukseen:

P11 = 12 000 + 750(11) = 20 250 hirveä

Katso lisää tästä esimerkistä täältä.

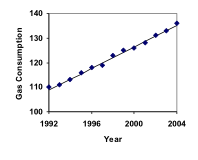
Bensiininkulutus Yhdysvalloissa on kasvanut tasaisesti. Alla on esitetty kulutustiedot vuosilta 1992-2004. Etsi malli näille tiedoille ja käytä sitä ennustamaan kulutusta vuonna 2016. Jos suuntaus jatkuu, milloin kulutus saavuttaa 200 miljardia gallonaa?

Vuosi ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Kulutus (mrd. gallonaa) 110 111 113 116 118 119 123 125 125 126 128 131 133 136
Näytä ratkaisu

Tämän datan kuvaaminen, se näyttää olevan suunnilleen lineaarinen suhde:

Vaikka on olemassa edistyneempiä tilastollisia tekniikoita, joita voidaan käyttää yhtälön löytämiseen datan mallintamiseksi, saadaksemme käsityksen siitä, mitä on tapahtumassa, voimme löytää yhtälön käyttämällä kahta datan osaa – kenties dataa vuosilta 1993 ja 2003.

Jos n = 0 vastaisi vuotta 1993, saataisiin P0 = 111 miljardia gallonaa.

Löytääksemme d:n meidän on tiedettävä, kuinka paljon kaasun kulutus keskimäärin kasvoi vuosittain. Vuodesta 1993 vuoteen 2003 kaasun kulutus kasvoi 111 miljardista gallonasta 133 miljardiin gallonaan, eli muutos oli yhteensä 133 – 111 = 22 miljardia gallonaa 10 vuoden aikana. Tämä antaa meille keskimääräiseksi muutokseksi 22 miljardia gallonaa / 10 vuotta = 2,2 miljardia gallonaa vuodessa.

Yhtäläisesti,

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 miljardia gallonaa vuodessa

Voidaan nyt kirjoittaa yhtälömme haluamassamme muodossa.

Rekursiivinen muoto

P0 = 111

Pn = Pn-1 + 2.2

Explisiittinen muoto

Pn = 111 + 2.2n

Laskemalla arvot eksplisiittistä muotoa käyttäen ja piirtämällä ne yhteen alkuperäisen datan kanssa nähdään, kuinka hyvin mallimme sopii dataan.

Voitamme nyt käyttää malliamme ennusteiden tekemiseen tulevaisuudesta olettaen, että aiempi suuntaus jatkuu ennallaan. Ennustamme bensiinin kulutusta vuonna 2016:

n = 23 (2016 – 1993 = 23 vuotta myöhemmin)

P23 = 111 + 2.2(23) = 161.6

Mallimme ennustaa, että Yhdysvallat kuluttaa 161.6 miljardia gallonaa bensiiniä vuonna 2016, jos nykyinen suuntaus jatkuu.

Tullaksemme selville, milloin kulutus nousee 200 miljardiin gallonaan, asettaisimme Pn = 200 ja ratkaisisimme n:n:

Pn = 200 Korvaamme Pn:n mallillamme

111 + 2.2n = 200 Vähennä molemmista puolista 111

2,2n = 89 Jaa molemmat puolet 2,2:lla

n = 40,4545

Tämä kertoo, että kulutus saavuttaa 200 miljardin noin 40 vuotta vuoden 1993 jälkeen, eli vuonna 2033.

Vaiheet, joilla tähän vastaukseen päästään, on esitetty yksityiskohtaisesti seuraavassa videossa.

Kuntosalijäsenyyden kustannukset dollareina n kuukaudeksi voidaan kuvata eksplisiittisellä yhtälöllä Pn = 70 + 30n. Mitä tämä yhtälö kertoo meille?

Näytä ratkaisu

P0:n arvo tässä yhtälössä on 70, joten alkuperäinen aloituskustannus on 70 dollaria. Tämä kertoo meille, että kuntosalille liittymisestä on maksettava 70 dollarin alku- tai käynnistysmaksu.

Yhtälön arvo d on 30, joten kustannukset kasvavat 30 dollarilla joka kuukausi. Tämä kertoo meille, että kuntosalin kuukausittainen jäsenmaksu on 30 dollaria kuukaudessa.

Tämän esimerkin selitys on esitetty tarkemmin alla.

Kokeile

Kanadassa kotona olevien isien määrä on kasvanut tasaisesti. Vaikka suuntaus ei ole täysin lineaarinen, se on melko lineaarinen. Etsi vuosien 1976 ja 2010 tietojen avulla eksplisiittinen kaava kotiin jäävien isien lukumäärälle ja ennusta sen avulla lukumäärä vuonna 2020.

Vuosi 1976 1984 1991 2000 2010
# of Stay -at-home fathers 20610 28725 43530 47665 53555
Näytä ratkaisu

Asettamalla n= 0 vastaamaan vuotta 1976, niin P_0= 20 610.
Vuosina 1976-2010 kotiin jäävien isien määrä kasvoi 53 555 – 20 610 = 32 945
Tämä tapahtui 34 vuoden aikana, jolloin yhteinen eri d on 32 945 / 34 = 969.
P_n= 20 610 + 969n
Ennustetaan vuodelle 2020, käytämme n = 44, P(44) = 20 610 + 969(44) = 63 246 koti-isää vuonna 2020.

Kun hyvät mallit menevät pieleen

Kun käytät matemaattisia malleja ennustamaan tulevaa käyttäytymistä, on tärkeää pitää mielessä, että hyvin harvat trendit jatkuvat loputtomiin.

Esimerkki

Esitettäköön, että nelivuotias poika on tällä hetkellä 39 tuumaa pitkä, ja sinun käsketään olettaa hänen kasvavan 2,5 tuumaa vuodessa.

Voidaan asettaa kasvumalli, jossa n = 0 vastaa 4 vuoden ikää.

Rekursiivinen muoto

P0 = 39

Pn = Pn-1 + 2.5

Explisiittinen muoto

Pn = 39 + 2.5(n)

Siten 6-vuotiaana odotamme hänen olevan

P2 = 39 + 2.5(2) = 44 tuumaa pitkä

Mikä tahansa matemaattinen malli hajoaa lopulta. Varmasti meidän ei pitäisi odottaa, että tämä poika jatkaisi kasvuaan samalla nopeudella koko elämänsä ajan. Jos näin tapahtuisi, hän olisi 50-vuotiaana

P46 = 39 + 2.5(46) = 154 tuumaa pitkä = 12.8 jalkaa pitkä!

Käyttäessämme mitä tahansa matemaattista mallia, meidän on harkittava, mitä syötteitä on järkevää käyttää. Aina kun ekstrapoloimme tai teemme ennusteita tulevaisuuteen, oletamme, että malli on jatkossakin pätevä.

Katsokaa videon selitys tästä lineaarisen kasvumallin jaottelusta täältä.

Eksponentiaalinen (geometrinen ) kasvu

Populaatiokasvu

Esitettäköön, että joka vuosi vain 10 %:lla järvessä olevasta kalamäärästä syntyy eloonjääneitä jälkeläisiä. Jos järvessä oli viime vuonna 100 kalaa, nyt kaloja olisi 110. Jos järvessä oli viime vuonna 1000 kalaa, nyt kaloja olisi 1100. Ilman estäviä tekijöitä ihmis- ja eläinpopulaatioilla on taipumus kasvaa vuosittain prosentilla olemassa olevasta populaatiosta.


Esitettäköön, että järvessämme oli aluksi 1000 kalaa, ja 10 %:lla kaloista on joka vuosi elossa olevia jälkeläisiä. Koska aloitamme 1000 kalalla, P0 = 1000. Miten laskemme P1:n? Uusi populaatio on vanha populaatio, johon on lisätty 10 %. Symbolisesti:

P1 = P0 + 0.10P0

Huomaa, että tämä voidaan tiivistää lyhyempään muotoon faktoroimalla:

P1 = P0 + 0.10P0 = 1P0 + 0.10P0 = (1+ 0.10)P0 = 1.10P0

Vaikka 10 %:n kasvu on kasvuvauhti, niin vastaavasti kasvukerroin on 1.10. Huomaa, että 1,10 voidaan ajatella olevan ”alkuperäinen 100 % plus 10 % lisää.”

Kalapopulaatiomme osalta

P1 = 1,10(1000) = 1100

Voisimme sitten laskea populaation myöhempinä vuosina:

P2 = 1.10P1 = 1.10(1100) = 1210

P3 = 1.10P2 = 1.10(1210) = 1331

Huomaa, että ensimmäisenä vuonna populaatio kasvoi 100 kalalla, toisena vuonna populaatio kasvoi 110 kalalla ja kolmantena vuonna 121 kalalla.

Vaikka prosentuaalinen kasvu on jatkuvaa, kalojen määrän todellinen kasvu kasvaa joka vuosi.

Kuvaamalla näitä arvoja huomaamme, että tämä kasvu ei näytä aivan lineaariselta.

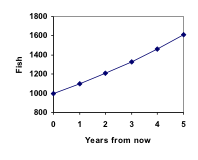
Tämän kalaskenaarion läpikäyntiä voi katsoa täältä:

Voidaksemme saada paremman kuvan siitä, miten tämä prosentuaaliseen kasvuun perustuva kasvu vaikuttaa asioihin, tarvitsemme eksplisiittisen muodon, jotta voimme nopeasti laskea arvot kauemmas tulevaisuuteen.

Kuten teimme lineaarisen mallin kohdalla, aloitamme rakentamisen rekursiivisesta yhtälöstä:

P1 = 1.10(P0 )= 1.10(1000)

P2 = 1.10(P1 )= 1.10(1.10(1000)) = 1.102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Havaitessamme kaavan voimme yleistää eksplisiittisen muodon muotoon:

Pn = 1.10n(1000), tai vastaavasti Pn = 1000(1.10n)

Tästä voimme nopeasti laskea kalojen määrän 10, 20 tai 30 vuodessa:

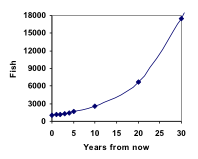
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Lisäämällä nämä arvot kuvaajaamme paljastuu muoto, joka ei todellakaan ole lineaarinen. Jos kalapopulaatiomme olisi kasvanut lineaarisesti, 100 kalan verran joka vuosi, populaatio olisi saavuttanut 30 vuodessa vain 4000 kalaa, kun taas tällä prosentuaaliseen kasvuun perustuvalla kasvulla, jota kutsutaan eksponentiaaliseksi kasvuksi, populaatio olisi kasvanut lähes 18000 kalaa.

Videon, joka havainnollistaa eksplisiittistä mallia tästä kalajutusta, voi katsoa täältä:

Exponentiaalisessa kasvussa populaatio kasvaa suhteessa populaation kokoon, joten populaation kasvaessa suuremmaksi sama prosentuaalinen kasvu tuottaa suuremman numeerisen kasvun.

Exponentiaalinen kasvu

Jos määrä alkaa koosta P0 ja kasvaa R % (kirjoitettuna desimaalilukuna, r) jokaisella aikajaksolla, niin määrä n aikajakson jälkeen voidaan määrittää jommankumman näistä suhteista avulla:

Rekursiivinen muoto

Pn = (1+r) Pn-1

Explisiittinen muoto

Pn = (1+r)n P0 tai vastaavasti Pn = P0 (1+r)n

Kutsumme r:ää kasvunopeudeksi.

Termiä (1+r) kutsutaan kasvukertoimeksi tai yleiseksi suhdeluvuksi.

Esimerkki

Vuosien 2007 ja 2008 välisenä aikana Olympia, WA kasvoi lähes 3 % 245 tuhannen asukkaan väestöön. Jos tämä kasvuvauhti jatkuisi, mikä olisi Olympian väkiluku vuonna 2014?

Näytä ratkaisu

Kuten aiemminkin, meidän on ensin määriteltävä, mikä vuosi vastaa vuotta n = 0. Koska tiedämme vuoden 2008 väkiluvun, olisi järkevää, että vuosi 2008 vastaa vuotta n = 0, joten P0 = 245 000. Vuosi 2014 olisi tällöin n = 6.

Tiedämme, että kasvuvauhti on 3 %, jolloin r = 0,03.

Käyttämällä eksplisiittistä muotoa:

P6 = (1+0,03)6 (245 000) = 1,19405(245 000) = 292 542,25

Malli ennustaa, että vuonna 2014 Olympiassa olisi noin 293 tuhatta ihmistä.

Seuraavalla videolla selitetään tämä esimerkki yksityiskohtaisesti.

Eksponenttien arvioiminen laskimella

Tällaisten lausekkeiden kuin (1,03)6 arvioimiseksi on helpompi käyttää laskinta kuin kertoa 1,03 kuusi kertaa itsellään. Useimmissa tieteellisissä laskimissa on painike eksponentteja varten. Se on tyypillisesti joko merkitty seuraavasti:

^ , yx tai xy .

Arvioidaksemme 1,036 kirjoittaisimme 1,03 ^ 6 tai 1,03 yx 6. Kokeile – sinun pitäisi saada vastaus noin 1.1940523.

Kokeile

Intia on maailman toiseksi väkirikkain maa, ja sen väkiluku vuonna 2008 oli noin 1,14 miljardia ihmistä. Väestö kasvaa vuosittain noin 1,34 %. Jos tämä suuntaus jatkuu, kuinka suureksi Intian väkiluku kasvaa vuoteen 2020 mennessä?

Näytä ratkaisu

Käytettäessä vuotta 2008 vastaavaa n = 0 saadaan P_12= (1+0,0134)12(1,14) = noin 1.337 miljardia ihmistä vuonna 2020

Esimerkkejä

Ystävä käyttää yhtälöä Pn = 4600(1.072)n ennustaakseen paikallisen korkeakoulun vuotuisia lukukausimaksuja. Hän sanoo, että kaava perustuu vuoden 2010 jälkeisiin vuosiin. Mitä tämä yhtälö kertoo meille?

Näytä ratkaisu

Yhtälössä P0 = 4600, joka on lukukausimaksun lähtöarvo, kun n = 0. Tämä kertoo, että lukukausimaksu vuonna 2010 oli 4600 dollaria.

Kasvukerroin on 1,072, joten kasvuvauhti on 0,072 eli 7,2 %. Tämä kertoo meille, että lukukausimaksun odotetaan kasvavan 7,2 % joka vuosi.

Seuraavasti voimme sanoa, että lukukausimaksu vuonna 2010 oli 4600 dollaria, ja sen odotetaan kasvavan 7,2 % joka vuosi.

Katsokaa seuraavassa tämä esimerkki työstettynä.

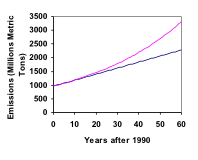
Vuonna 1990 kotitalouksien energiankulutus USA:ssa aiheutti 962 miljoonaa tonnia hiilidioksidipäästöjä. Vuoteen 2000 mennessä tämä määrä oli noussut 1182 miljoonaan metriseen tonniin. Jos päästöt kasvavat eksponentiaalisesti ja jatkuvat samaa vauhtia, kuinka suureksi päästöt kasvavat vuoteen 2050 mennessä?

Näytä ratkaisu

Samoin kuin aiemminkin, vastaamme n = 0:aa vuodelle 1990, koska se on ensimmäisen hallussamme olevan tiedon vuosi. Tällöin P0 = 962 (miljoonaa tonnia hiilidioksidia). Tässä ongelmassa meille ei anneta kasvuvauhtia, vaan sen sijaan meille annetaan, että P10 = 1182.

Kun n = 10, eksplisiittinen yhtälö näyttää seuraavalta:

P10 = (1+r)10 P0

Me tiedämme P0:n arvon, joten voimme laittaa sen yhtälöön:

P10 = (1+r)10 962

Tiedämme myös, että P10 = 1182, joten korvatessamme sen saamme

1182 = (1+r)10 962

Voimme nyt ratkaista tämän yhtälön kasvunopeuden, r, suhteen. Aloitetaan jakamalla 962:lla.

\frac{1182}{962}={{(1+r)}^{10}}} Ota molemmista puolista 10. juuri

\sqrt{\frac{1182}{962}}=1+r Vähennä molemmista puolista 1

r=\sqrt{\frac{1182}{962}}-1=0.0208 = 2.08%

Jos päästöt kasvavat eksponentiaalisesti, ne kasvavat siis noin 2.08% vuodessa. Voimme nyt ennustaa päästöt vuonna 2050 löytämällä P60

P60 = (1+0,0208)60 962 = 3308,4 miljoonaa tonnia hiilidioksidia vuonna 2050

Katso lisää tästä esimerkistä täällä.

Pyöristäminen

Huomautuksena pyöristämisestä, huomaa, että jos olisimme pyöristäneet kasvuvauhdin 2,1 %:iin, laskelmamme vuoden 2050 päästöistä olisi ollut 3347. Pyöristäminen 2 prosenttiin olisi muuttanut tuloksemme 3156:een. Hyvin pieni ero kasvuvauhdissa suurenee suuresti eksponentiaalisessa kasvussa. Tästä syystä on suositeltavaa pyöristää kasvuvauhti mahdollisimman vähän.

Jos joudut pyöristämään, pidä vähintään kolme merkitsevää numeroa – numerot mahdollisten etunollien jälkeen. Niinpä 0,4162 voidaan järkevästi pyöristää 0,416:ksi. Kasvunopeus 0,001027 voitaisiin kohtuullisesti pyöristää 0,00103:ksi.

Juurten laskeminen laskimella

Edellisessä esimerkissä meidän piti laskea luvun 10. juuri. Tämä on eri asia kuin perusneliöjuuren, √, ottaminen. Monissa tieteellisissä laskimissa on painike yleisiä juuria varten. Se on tyypillisesti merkitty seuraavasti:

\sqrt{x}

Arvioidaksemme esimerkiksi 8:n 3. juuren, kirjoittaisimme joko 3 \sqrt{{{}} 8, tai 8 \sqrt{{{}} 3, laskimesta riippuen. Kokeile omallasi, kumpaa käytät – vastaukseksi pitäisi saada 2.

Jos laskimessasi ei ole yleistä juuripainiketta, kaikki ei ole menetetty. Voit sen sijaan käyttää eksponenttien ominaisuutta, jonka mukaan:

\sqrt{a}={a}^{\frac{1}{2}}.

Laskimesi eksponenttinäppäimellä voit siis laskea 8:n 3. juuren ja arvioida 81/3. Tee tämä kirjoittamalla:

8 yx ( 1 ÷ 3 )

Sulkeet kertovat laskimelle, että se jakaa 1/3:n ennen eksponentin tekemistä.

Kokeile

Yhteisöverkkosivuston käyttäjämäärä oli 45 tuhatta käyttäjää helmikuussa, kun se virallisesti julkistettiin, ja se kasvoi 60 tuhanteen lokakuuhun mennessä. Jos sivusto kasvaa eksponentiaalisesti ja kasvu jatkuu samaa vauhtia, kuinka monta käyttäjää on odotettavissa kaksi vuotta pörssiin tulon jälkeen?

Näytä ratkaisu

Tässä mitataan n kuukausina eikä vuosina, jolloin n = 0 vastaa helmikuun ajankohtaa, jolloin sivusto tuli pörssiin. Näin saadaan P_0= 45 tuhatta. Lokakuu on 8 kuukautta myöhemmin, joten P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ tai }3.66%
Yleinen eksplisiittinen yhtälö on P_n =(1.0366)^{n}45. Ennustamalla 24 kuukautta niiden julkistamisen jälkeen saadaan P_{24}=(1.0366)^{24}45=106,63 tuhatta käyttäjää.

Esimerkki

Vertailun vuoksi edelliseen esimerkkiin palatakseni, mitkä olisivat hiilidioksidipäästöt vuonna 2050, jos päästöt kasvaisivat lineaarisesti samaa tahtia?

Näytä ratkaisu

Tälleen saamme n = 0 vastaa vuotta 1990, jolloin P0 = 962. Löytääksemme d:n voisimme käyttää samaa lähestymistapaa kuin aiemmin ja todeta, että päästöt kasvoivat 220 miljoonaa tonnia kymmenessä vuodessa, jolloin yhteinen ero on 22 miljoonaa tonnia vuodessa.

Vaihtoehtoisesti voisimme käyttää samanlaista lähestymistapaa kuin käytimme eksponenttiyhtälön löytämiseksi. Kun n = 10, eksplisiittinen lineaarinen yhtälö näyttää seuraavalta:

P10 = P0 + 10d

Me tiedämme P0:n arvon, joten voimme laittaa sen yhtälöön:

P10 = 962 + 10d

Koska tiedämme, että P10 = 1182, korvaamalla sen saamme

1182 = 962 + 10d

Voimme nyt ratkaista tämän yhtälön yhteisen erotuksen d suhteen.

1182 – 962 = 10d

220 = 10d

d = 22

Tämä kertoo meille, että jos päästöt muuttuvat lineaarisesti, ne kasvavat 22 miljoonalla tonnilla joka vuosi. Ennustetaan päästöt vuonna 2050,

P60 = 962 + 22(60) = 2282 miljoonaa tonnia.

Huomaa, että tämä luku on huomattavasti pienempi kuin eksponentiaalisen kasvun mallin ennuste. Useampien arvojen laskeminen ja piirtäminen auttaa havainnollistamaan eroja.

Demonstraatio tästä esimerkistä on nähtävissä seuraavalla videolla.

Miten siis tiedämme, mitä kasvumallia käyttää, kun työskentelemme datan kanssa? On olemassa kaksi lähestymistapaa, joita tulisi käyttää yhdessä aina kun se on mahdollista:

  1. Etsitään enemmän kuin kaksi dataa. Piirrä arvot ja etsi trendi. Näyttääkö data muuttuvan viivan tavoin, vai näyttävätkö arvot kaartuvan ylöspäin?
  2. Harkitse dataan vaikuttavia tekijöitä. Ovatko ne asioita, joiden odotat muuttuvan lineaarisesti vai eksponentiaalisesti? Esimerkiksi hiilidioksidipäästöjen tapauksessa voisi olettaa, että jos muita tekijöitä ei ole, ne olisivat tiiviisti sidoksissa väestöarvoihin, joilla on taipumus muuttua eksponentiaalisesti.

By: adminPosted on

Vastaa

Sähköpostiosoitettasi ei julkaista.