Wie viele Seiten hat ein Kreis?

Es handelt sich um eine Hausaufgabe aus der Grundschule, die unter erfahrenen Mathematikern für Unstimmigkeiten sorgt. Um die richtige Antwort zu finden, habe ich mich auf das strengste aller wissenschaftlichen Instrumente berufen, die Twitter-Umfrage:

Im Nachhinein bedauere ich, dass ich keine „keine der oben genannten“ Optionen angegeben habe, aber dazu später mehr. In diesem Beitrag werde ich diese drei Antworten (und „Keine der oben genannten“) durchgehen und ihre Vor- und Nachteile aus meiner Sicht diskutieren, bevor ich auf dramatische Weise die richtige Antwort verrate.

Aber zuerst: Warum können wir nicht einfach die richtige Antwort geben? Die Worte in der Frage sind kaum geheimnisvoll. Wir alle wissen, was ein „Kreis“ ist, was es bedeutet, „wie viele“ von etwas zu zählen, und was eine „Seite“ ist … oder etwa nicht? Hier sind die (groben) Definitionen, die ich aus Gesprächen mit zwei Grundschülern destilliert habe, die mit dieser Frage konfrontiert worden waren:

1. Eine Linie, die einen Teil der Begrenzung einer Form einer ebenen Figur bildet.

Dass wir hier von einer ebenen Figur und nicht von einer „Form“ sprechen, liegt daran, dass wir Formen wollen, die in zwei Dimensionen leben (z. B. Quadrate oder Kreise, aber keine Kugeln oder Würfel). Die nächste Frage ist, was eine „Linie“ in Definition 1 ist. Hier ist eine Variante, die das festlegt:

2. Eine gerade Linie, die einen Teil der Begrenzung einer ebenen Figur bildet.

Wenn du „define: side“ in Google eingibst, ist die relevanteste Definition:

Eine geradlinige Figur ist eine, die aus geraden Linien besteht. Diese Definition ist also eine weitere Verfeinerung von Definition 2 und erlaubt es uns zu behaupten, dass ein Quadrat vier Seiten hat, sagt aber nichts über nicht-geradlinige ebene Figuren wie Kreise aus.

Unendlich viele Seiten?

Ich denke, es ist eine sichere Wette, dass die Teilnehmer an meiner Twitter-Umfrage ein höheres Niveau an mathematischer Bildung haben als der nationale Durchschnitt. Die Tatsache, dass sie bei dieser Frage geteilter Meinung waren und dass eine kleine Mehrheit eine Antwort wählte, die für die übliche Zielgruppe dieser Frage (Grundschüler) so gut wie nicht verfügbar ist, lässt darauf schließen, dass irgendwo etwas schief läuft.

So, hat ein Kreis unendlich viele Seiten? Es ist auf jeden Fall sinnvoll, einen Kreis als die Grenze von n-seitigen Polygonen zu betrachten, wenn n immer größer wird. Das ist genau der Ansatz, den Archimedes, Liu Hui und zahllose andere im Laufe der Jahrhunderte verwendet haben, um die Kreisgeometrie zu studieren und Näherungswerte für π zu finden.

Eine Ausgabe des Jiuzhang suanshu (Neun Kapitel über die mathematische Kunst) aus der Ming-Dynastie des 16.

Manchmal ist es absolut vernünftig, sich einen Kreis als ein Polygon mit unendlich vielen Seiten vorzustellen.

Als unerträglicher Pedant unter den Mathematikern möchte ich jedoch zwischen bequemer Kurzschrift und wörtlicher Wahrheit unterscheiden. Wenn wir darauf beharren, dass ein Kreis wirklich ein Polygon mit unendlich vielen Seiten ist, dann stellt sich die Frage: Was sind die Seiten? Und die einzig plausible Antwort lautet: die einzelnen Punkte des Kreises. Wie lang sind diese sogenannten Seiten? Null Zentimeter. Und sind diese Seiten durch Ecken getrennt? Offenbar nicht, entweder gibt es überhaupt keine Ecken, oder jeder Punkt ist sowohl eine Seite als auch eine Ecke.

Ich würde sagen, Seiten der Länge Null sind… ein problematisches Konzept. Wie kann man feststellen, ob man welche hat? Nehmen wir zum Beispiel an, ich studiere ein System, in dem ein Quadrat als Grenze von Achtecken wie diesem entsteht:

In dieser Situation könnte es für mich durchaus sinnvoll sein, mein Quadrat als ein Quadrat mit acht Seiten zu betrachten, von denen vier die Länge Null haben. Aber wenn ich darauf bestehen würde, dass mein (ganz gewöhnliches) Quadrat wirklich acht Seiten hat, würden Sie vielleicht eine Augenbraue hochziehen.

Diese Antwort – die siegreiche in meiner Umfrage – ist also die einzige, die ich für definitiv falsch erklären werde, während sie auch die einzige ist, die überhaupt eine geometrische Erkenntnis bietet. Ein Paradoxon? Nicht wirklich. Analoges Denken ist eine wertvolle Fähigkeit in der Mathematik und im Leben; gleichzeitig ist es wichtig, an der Erkenntnis festzuhalten, dass es das ist, was wir tun.

Für unendlich viele Seiten: geometrisch erhellend.
Gegen unendlich viele Seiten: achtseitige Quadrate.

Auf einer Tangente 1: Apeirogone

Auch wenn ein Kreis keiner ist, gibt es so etwas wie Polygone mit unendlich vielen Seiten? Nun, es gibt ein Wort, um so etwas zu beschreiben: ein Apeirogon. Ein regelmäßiges Apeirogon hätte dann Seiten von gleicher Länge (ungleich Null) mit gleichen Winkeln dazwischen. Die einzige Möglichkeit ist dieses verblüffend unaufregende Objekt:

Wenn Sie einwenden, dass es sich hierbei um ein „Polygon“ handelt (entweder wegen der Winkel von 180° oder der nicht in einer Schleife schließenden Kantenkette), wie wäre es mit etwas wie diesem: Beginnen Sie am unteren Ende eines Kreises und bewegen Sie sich in jeder Phase um die Hälfte des verbleibenden Kreises und ersetzen Sie den soeben zurückgelegten Bogen durch eine gerade Kante:

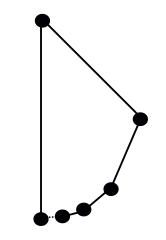
Ist das ein echtes Polygon? Auch hier kommt es auf Ihre Begriffe an. Nach einer gängigen Definition, der einer „geschlossenen polygonalen Kette“, ist dies kein echtes Polygon, da die Anfangsecke (unten links) nur mit einer Kante verbunden ist. Dieser Punkt ist die Grenze einer Folge von Kanten von rechts, was diese Form zu einer „sich nicht selbst schneidenden, stückweise linearen, geschlossenen Kurve“ macht, einer anderen Definition von Polygon, die von vielen verwendet wird.

Wenn wir unsere gewohnte euklidische Welt verlassen und in den hyperbolischen Raum eintreten, gibt es keine Zweideutigkeit. Apeirogone (sogar regelmäßige Apeirogone) existieren einfach:

Eine Kachelung der hyperbolischen Ebene durch regelmäßige Apeirogone. (Von Anton Sherwood – Eigenes Werk, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Ab auf eine Tangente 2: Extrempunkte

Es ist vielleicht vertretbarer zu sagen, dass ein Kreis unendlich viele Ecken hat als unendlich viele Seiten (obwohl dies eine Frage ist, die nicht sehr oft gestellt zu werden scheint). Zunächst einmal: Wenn eine Ecke eines Quadrats ein Punkt ist, an dem die Begrenzungslinie nicht gerade ist, dann erfüllt jeder Punkt auf dem Kreis diese Bedingung. Etwas komplizierter ist der Begriff des Extrempunkts einer Form: Das ist jeder Punkt, durch den man ein Geradensegment ziehen kann, das die Form nur in genau diesem Punkt berührt. Bei einem Quadrat und vielen anderen bekannten Formen fallen die Extrempunkte genau mit den Ecken zusammen. Jeder Punkt auf der Begrenzung des Kreises ist ein Extrempunkt, also ist es sicher wahr, dass ein Kreis unendlich viele hat.

Wir könnten uns Sorgen machen, dass einige Formen wie dieser Chevron Ecken haben, die keine Extrempunkte sind:

Hier ist die untere mittlere Ecke kein Extrempunkt (die anderen drei Ecken schon). Das Problem ist, dass diese Form nicht konvex ist (grob gesagt, stehen einige Teile zu weit heraus). Ein Kreis ist konvex, also brauchen wir uns vielleicht keine Sorgen zu machen. Alternativ könnten wir das Problem lösen, indem wir eine „Ecke“ als einen Punkt definieren, der ein Extrempunkt entweder der fraglichen Form oder ihres Komplements ist, d. h. der gesamten Ebene, aus der die Form ausgeschnitten ist. Auf diese Weise würden die Ecken aller Polygone, einschließlich des Chevrons, erkannt. Bei glatten Kurven würden alle Grenzpunkte als „Ecken“ identifiziert, mit Ausnahme von Wendepunkten (was nicht unvernünftig ist, da man argumentieren könnte, dass die Grenze dort gerade ist).

Eine Seite?

In der Grundschule scheint es, dass „eine“ die Antwort ist, die angekreuzt wird. Und es gibt eine einigermaßen vernünftige Begründung dafür. Erinnern Sie sich an Definition 1 oben:

1. Eine Linie, die einen Teil der Begrenzung einer ebenen Figur bildet.

Die unmittelbare Frage ist, was als „Linie“ zählt, insbesondere wenn wir nicht auf Geradheit bestehen. Wenn wir das zu locker sehen, dann könnte man sagen, dass jede ebene Figur „eine Seite“ hat, in demselben Sinne, in dem sie eine Begrenzung, einen Umfang oder einen Umkreis hat. Aber das muss falsch sein, denn wir wollen doch, dass ein Quadrat vier Seiten hat. Nun, ein Quadrat hat vier Punkte, an denen es nicht glatt ist, mit vier glatten Abschnitten dazwischen. Vielleicht waren es wirklich die glatten Abschnitte, die wir die ganze Zeit gezählt haben. Wir haben also implizit eine neue Verfeinerung der Definition 1 (und nutzen die Gelegenheit, den vagen Begriff „Figur“ zu streichen):

4. Jeder glatte Abschnitt einer stückweise glatten geschlossenen Kurve.

Eine „geschlossene Kurve“ ist eine Kurve, die in einer Schleife auf sich selbst trifft, so dass sie keine freien Enden hat. „Stückweise glatt“ bedeutet, dass sie aus glatten Abschnitten aufgebaut ist, die sich an isolierten, nicht glatten Punkten treffen. Es ist völlig legitim, die glatten Abschnitte der Begrenzung einer solchen Form zählen zu wollen, und es ist keineswegs abwegig, dabei das Wort „Seite“ zu verwenden. Ich behaupte also nicht, dass dies definitiv die falsche Antwort ist.

Die Frage ist, ob diese Interpretation von „Seite“ nicht nur kohärent, sondern auch natürlich genug ist, dass sie einfach vorausgesetzt werden kann, ohne dass sie explizit gesagt wird (was selten bis nie der Fall ist). Was passiert, wenn Glattheit und Geradheit nicht übereinstimmen? Betrachten wir diese Grabsteinform, die entsteht, wenn man den oberen Teil eines Quadrats durch einen Halbkreis mit gleichem Durchmesser ersetzt.

Dieser hat zwei glatte Abschnitte (die untere Linie und den Rest), aber drei gerade Kanten (plus ein gebogenes Stück, das zwei davon glatt verbindet). Wie viele Seiten hat es also? Ich habe wieder meine Twitter-Freunde befragt:

Diesmal hätte ich „unendlich viele“ als Option angeben sollen, obwohl das in „keine der oben genannten“ aufgehen kann. Jeder, der dafür stimmt, dass der Kreis unendlich viele Seiten hat, sollte hier automatisch mit „Keiner der oben genannten“ stimmen, es sei denn – ein wichtiger Vorbehalt – die Natur dieser Form weist den Leser auf eine andere Vorstellung von „Seite“ hin. Die Tatsache, dass die beliebtesten Antworten in diesen beiden Umfragen unvereinbar sind, deutet darauf hin, dass dies der Fall sein könnte (oder verstärkt zumindest die Unklarheit).

Obwohl zwei eine durchaus respektable Antwort ist, die mit der obigen Definition 4 und der Einseitigkeit eines Kreises vereinbar ist, bin ich nicht überzeugt, dass sie definitiv die richtige ist oder dass drei oder vier kategorisch falsch sind. Es kommt darauf an, was man zählen will: glatte Abschnitte, gerade Kanten oder gerade Kanten plus das, was dann übrig bleibt, wobei je nach Kontext jede davon die gewünschte Antwort sein kann (mehr dazu unten). In diesem Zusammenhang bin ich mir nicht sicher, ob das Zählen der glatten Abschnitte meiner Intuition des Wortes „Seite“ vollständig entspricht. Immerhin befinden sich die beiden aufrechten Abschnitte des Grabsteins – ich denke, man kann sagen – „auf gegenüberliegenden Seiten“. Sind wir wirklich damit zufrieden, dass sie gleichzeitig Teil der „gleichen Seite“ sind?

Man könnte einwenden, dass ich zwei verschiedene Bedeutungen von „Seite“ miteinander vermische, dass die Terminologie manchmal kollidiert und wir einfach damit leben müssen. Ich bin mir da aber nicht so sicher. Bei dieser Übung geht es darum, von einer Situation (geradlinige Figuren) auszugehen, in der die beiden Begriffe ziemlich gut ineinandergreifen. Wenn es eine neue Idee gäbe, die alles beinhaltet, was uns am Original gefällt, die aber auch auf eine breitere Kategorie von Formen anwendbar ist, dann hätte diese Idee einen überwältigenden Anspruch darauf, die einzig richtige Antwort zu sein. Wenn aber alle unsere Verallgemeinerungsversuche dazu führen, dass wünschenswerte Aspekte des Originals geopfert werden, dann gibt es vielleicht keine einzige richtige Verallgemeinerung. Es gibt verschiedene Möglichkeiten mit unterschiedlichen Kompromissen, die in verschiedenen Kontexten geeignet sein könnten (und wenn wir uns in einer Situation befinden, in der mehr als eine im Spiel ist, dann könnten sie hilfreicherweise verschiedene Namen erhalten).

Hier ist eine weitere Variante: ein Weierstraß-Grabstein, der durch Ersetzen der oberen Kante eines Quadrats durch einen Abschnitt der Weiestress-Funktion erzeugt wird, eine unendlich gewundene Linie, die nirgendwo glatt ist.

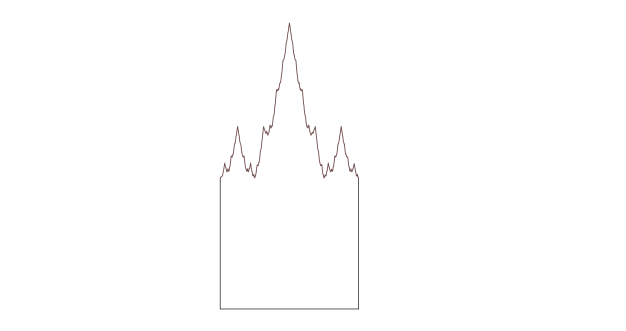
Hier (und achten Sie auf den Tippfehler) ist, was meine Twitter-Freunde dazu sagten – obwohl weniger eine Meinung wagten:

Ungeachtet der Skepsis meiner Twitter-Follower werde ich gleich erklären, warum ich es nicht für albern halte, dies als vier Seiten zu sehen (von denen eine nicht glatt ist). Andererseits, wenn Sie glatte Seiten bevorzugen, dann haben Sie wiederum die Wahl zwischen der Sichtweise, dass es unendlich viele Seiten hat (von denen drei die Länge 1 haben und der Rest die Länge 0), oder dass es 3 Seiten plus eine Strecke hat, die definitiv keine Seite ist.

Für eine Seite: eine einzelne glatte Kurve.
Gegen eine Seite: dieselbe Seite auf gegenüberliegenden Seiten.

Auf einer Tangente 3: Seiten versus Kanten

Wie viele Seiten hat ein Quadrat? 4. Wie viele Kanten hat es? Vier. Sind also Kanten und Seiten das Gleiche? Nicht unbedingt. Hier sind zwei Konfigurationen, die – zumindest argumentativ – jeweils vierseitig sind, aber 5 bzw. 3 Kanten haben:

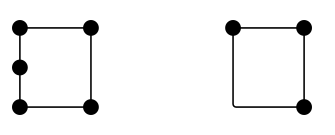
Im Allgemeinen würde ich sagen, dass eine „Kante“ ein topologisches Objekt ist, da ihre Funktion und nicht ihre Form entscheidend ist. Denken Sie an den Plan der Londoner U-Bahn. Bei der Frage, wie viele Kanten es in diesem Netz gibt, ist es nicht sinnvoll, gerade oder glatte Abschnitte aufzuzählen. Es sind die Verbindungen zwischen den Stationen (oder Eckpunkten), die zählen.

Wie bereits erwähnt, ist es üblich, sich ein Polygon als eine sehr einfache Art von Netz vorzustellen, das man eine geschlossene polygonale Kette nennt: eine Reihe von Eckpunkten (in diesem Fall die Ecken des Polygons), die mit Kanten so verbunden sind, dass jeder Eckpunkt auf genau zwei Kanten liegt und das Ganze eine einzige Schleife bildet. In diesem Fall stimmen Kanten und Seiten sowie Eckpunkte und Ecken überein. Aber im Allgemeinen kann man diese Übereinstimmung aufheben, wie in den beiden kleinen Netzen oben.

Wenn man netzwerktheoretisch denken will, aber die Scheitelpunkte nicht klar markiert sind, dann muss man raten, wo sie sind. Bei einem Polygon ist das einfach – die Scheitelpunkte befinden sich an den Ecken -, weshalb der Wechsel zwischen geometrischen und topologischen Ansätzen so selbstverständlich ist. Bei anderen Formen, wie z. B. den beiden oben genannten Grabsteinen, ist dies jedoch nicht so offensichtlich. Dennoch, in jedem Fall, wenn man Ihnen sagt, dass es irgendwo Scheitelpunkte gibt, und Sie auffordert, diese zu lokalisieren, denke ich, dass es vernünftig wäre, zu vermuten, dass es vier sind, nämlich die Ecken des ursprünglichen Quadrats, und dass die obere Kante aus irgendeinem Grund als eine nicht-gerade Linie dargestellt wurde. Und wenn wir die Dinge so sehen wollen, dass jeder der Grabsteine 4 Kanten hat, dann könnte das ungünstig erscheinen (obwohl logisch kohärent!), darauf zu bestehen, dass sie eine andere Anzahl von Seiten haben (zumal die obere Seite – trotz ihrer eigenen Geometrie – eindeutig „auf einer Seite“ der Figur liegt). Anstatt zu raten, fragte mich einer meiner Twitter-Korrespondenten: „Wurden beide oberen Scheitelpunkte entfernt?“, eine Frage, die nur aus netzwerktheoretischer Sicht Sinn macht.

Wo bleibt dann der Kreis? Das Problem ist, dass kein Punkt auf dem Kreis einen besseren Anspruch darauf hat, Scheitelpunkt zu sein als ein anderer. Obwohl es also verlockend (und wiederum kohärent) ist, einen Kreis als ein Netzwerk mit einer Kante zu betrachten, gibt es keinen offensichtlichen Grund, einen Punkt gegenüber einer anderen Zahl zu bevorzugen.

Könnten wir ihn als ein Netzwerk ohne Knotenpunkte betrachten, eine Art U-Bahn-Linie ohne Stationen? Die übliche mathematische Konzeption eines Netzwerks würde das nicht zulassen, aber das sollte uns nicht zu sehr abschrecken. Dies legt einen rein topologischen Ansatz nahe. Das Problem ist, dass aus dieser Sicht ein Kreis zwar eine Art Netzwerk ohne Eckpunkte und mit einer Kante sein kann, aber auch ein Quadrat (wenn die U-Bahn-Linie zufällig so angelegt ist). In der Topologie ist ein Quadrat ein Kreis. (Das ist kein Paradoxon, sondern besagt nur, dass die Begrenzung eine einzige Schleife ist, deren Form keine Rolle spielt). Während diese Art von Netzwerk also „eine Kante“ hat, hat ein Quadrat offensichtlich nicht „eine Seite“, so dass die Beziehung zwischen Seiten (geometrisch) und Kanten (topologisch) wieder einmal nicht stimmt, genau wie bei den beiden kleinen Netzwerken, die oben abgebildet sind. Dieser Ansatz bringt uns also nicht sehr weit.

Keine Seiten?

Es mag paradox erscheinen zu behaupten, dass ein Kreis (oder eine andere Form) „keine Seiten“ hat. Aber das Argument für die Verteidigung ist ganz einfach. Wir kehren zur Definition 2 zurück:

2. Eine gerade Linie, die einen Teil der Begrenzung einer ebenen Figur bildet.

Dies ist ein einfacher, leicht verständlicher Satz, der die Seiten eines Quadrats perfekt erfasst. Eine zufriedenstellende Verallgemeinerung auf gekrümmte Figuren haben wir nicht gefunden, also bleibt man am besten beim Original. Und ein Kreis hat keine.

Für keine Seiten: stimmt, nach einem vernünftigen Begriff von „Seite“.
Gegen keine Seiten: klingt wie ein Zen-Koan.

Keiner der oben genannten?

Erinnern Sie sich an die von Google gelieferte Definition:

3. Jede der Linien, die die Begrenzung einer ebenen geradlinigen Figur bilden.

Der Versuch, dies auf einen Kreis – eine nicht geradlinige Figur – anzuwenden, ergibt nichts. Die Frage ist so sinnlos wie „Wie viele Seiten hat der Montag?“

Da Definition 3 die offiziellste ist (die einzige in diesem Beitrag, die nicht von mir oder meinen Kindern erfunden wurde), ist dann nicht „Keine der oben genannten“ die kategorisch richtige Antwort? Mag sein. Andererseits: Wenn uns jemand eine Frage stellt, verlangt das Prinzip der Nächstenliebe vielleicht, dass wir davon ausgehen, dass sie sinnvoll ist, solange wir nicht eindeutig das Gegenteil beweisen können, und die Definitionen 1, 2, 4 und andere Varianten machen das möglich. Außerdem ist Definition 3 eher sprachlich als formal-mathematisch und daher eher deskriptiv als präskriptiv, so dass wir uns nicht an sie binden sollten.

Für nichts von alledem: semantische Fehlfunktion.
Gegen nichts von alledem: dialogische Nächstenliebe.

Die richtige Antwort

Was hat mich veranlasst, diesen Beitrag zu schreiben? Wie unzählige Grundschüler wurden auch meine fünfjährigen Zwillingssöhne – die eingangs erwähnten Grundschüler – vor kurzem bei den Hausaufgaben vor diese Frage gestellt. Der eine entschied sich für „1“, der andere für „0“, und ich habe versucht, ihre Argumentation oben einzufangen und zu erläutern. Ich denke, dass beide Antworten durchaus vertretbar sind – und keine davon ist definitiv richtig.

Was soll man also tun, wenn man die Frage gestellt bekommt: Wie viele Seiten hat ein Kreis? Meiner Meinung nach besteht die optimale Antwort darin, den Mathematiker in deinem Leben zu bitten, eine 3000 Wörter umfassende Abhandlung zu diesem Thema zu schreiben, die du dann ausdrucken und deinem unglücklichen Lehrer triumphierend überreichen kannst. Wenn das nicht gelingt, ist es am besten, dem Beispiel von Sokrates zu folgen und die Frage mit einer Gegenfrage zu beantworten: Was meinst du mit „Seite“?

Am Ende sagt uns das Zählen bis Null oder bis Eins oder die Weigerung, die Frage zu beantworten, so gut wie nichts über die Geometrie von Kreisen. Aber es gibt viel zu gewinnen, wenn man vertraute Begriffe auseinander nimmt, wenn man zusätzliche Bedingungen weglässt oder hinzufügt, wenn man unsere Intuition herausfordert, indem man von einem Kontext in einen etwas anderen wechselt, und wenn man versucht, genau aufzuschreiben, was wir mit einem bestimmten Begriff in einem bestimmten Umfeld meinen. Das ist es, worum es in der echten Mathematik geht.

Fußnoten

Man könnte auch etwas anderes machen: z.B. einen Ausgangspunkt P auf dem Kreis wählen, von dem aus man die Entfernung um den Umfang herum misst. Dann erklärst du, dass die Punkte, die einen rationalen Abstand von P haben, die Ecken sind und der Rest die Seiten. Dies hat zur Folge, dass es eine abzählbar unendliche Anzahl von Ecken und eine nicht abzählbar unendliche Anzahl von Seiten gibt. Man könnte auch das Gegenteil behaupten. Das könnte gut zum Ansatz der polygonalen Begrenzung von Kreisen passen, aber ich würde nicht zustimmen, dass es einfach oder offensichtlich genug ist, um als „die richtige Antwort“ zu gelten.

Einer meiner Twitter-Korrespondenten war besorgt darüber, wie glatt die Kurve ist. Dieser Grabstein ist kontinuierlich differenzierbar, aber nicht doppelt so. Es wäre sicher interessant, wenn viele Leute der Meinung wären, dass dies eine kritische Angelegenheit ist, und man könnte dies wahrscheinlich mit einem unendlich glatten Grabstein testen, der aus so etwas besteht, obwohl ich die Details noch nicht durchdacht habe.

Wir könnten versuchen, dies wie folgt zu formalisieren: In einem Quadrat (oder einem beliebigen Polygon) hat eine Seite die Eigenschaft, dass man, ausgehend von einer beliebigen Position im Inneren, die Form gerade durch die eigene Position schneiden kann, so dass die gewählte Seite fest auf einer Seite des Schnitts liegt. Bei einem zweiseitigen Grabstein funktioniert das nicht: Bei jedem Schnitt wird immer die lange Seite durchtrennt. Wir könnten dies abschwächen, indem wir sagen, dass es, um als Seite zu gelten, mindestens eine Möglichkeit geben muss, die Form so zu durchschneiden, dass die Seite auf einer Seite des Schnitts liegt. Damit könnten wir sagen, dass der Grabstein vier Seiten hat (auch wenn der gebogene Abschnitt nicht auf einer Seite der Punkte im oberen Bereich liegt). Für den Kreis gilt jedoch, dass seine vermeintliche eine Seite nie auf einer Seite liegt (also ausgeschlossen wäre), und nur der gerade Abschnitt eines Halbkreises würde als Seite zählen.

Es ist nicht einfach, eine strenge Begründung zu finden, die für beide Grabsteine gilt, aber ich denke eher informell im Sinne von Schelling-Punkten: d.h. Orte, die aus Gründen, die nicht leicht vorherzusagen sind, als besonders hervorstechen.

Dankeschön

Danke an alle, die an meinen Umfragen teilgenommen oder sie retweetet oder mit mir auf Twitter diskutiert haben.