Quadratursignale, auch IQ-Signale, IQ-Daten oder IQ-Samples genannt, werden häufig in HF-Anwendungen verwendet. Sie bilden die Grundlage für die Modulation und Demodulation komplexer HF-Signale, sowohl in Hardware als auch in Software, sowie für die Analyse komplexer Signale. Dieser Beitrag befasst sich mit dem Konzept der IQ-Signale und ihrer Verwendung.
Ein Paar periodischer Signale wird als „Quadratur“ bezeichnet, wenn sie sich in der Phase um 90 Grad unterscheiden. Das „gleichphasige“ oder Referenzsignal wird als „I“ bezeichnet, und das um 90 Grad verschobene Signal (das Signal in Quadratur) wird „Q“ genannt. Was bedeutet das und warum ist das wichtig? Beginnen wir mit einigen Grundlagen.
Grundlagen der HF-Modulation
Ich beginne mit einer Übersicht über die einfache HF-Modulation. Ein unmodulierter HF-Träger ist einfach eine Sinuskurve, wie unten gezeigt.
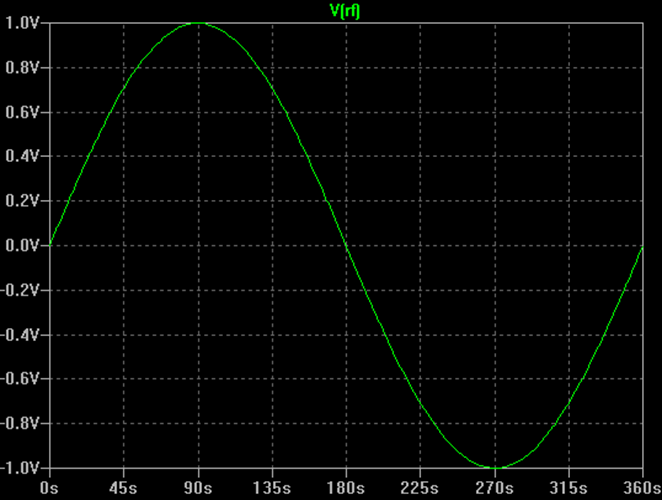
Das Signal kann als eine Funktion der Zeit durch die folgende Gleichung beschrieben werden:
V(t) = A * sin (2 * π * f * t + Ф)
wobei:
A: ist die Spitzenamplitude
f: ist die Frequenz
t: ist die Zeit
Ф: ist die Phasenverschiebung
Informationen werden von einem HF-Träger durch den Prozess der Modulation „getragen“. Das Informationssignal (Sprache, Daten usw.) wird verwendet, um die Eigenschaften des HF-Signals zu verändern. Ein einfaches Beispiel ist die Amplitudenmodulation (AM).
Bei AM wird das Informationssignal verwendet, um die Amplitude des Trägers zu verändern oder zu modulieren. Mathematisch lässt es sich darstellen, indem die Konstante „A“ in der vorherigen Gleichung in ein zeitlich veränderliches Signal (das Informationssignal) umgewandelt wird:
V(t) = A(t) * sin (2 * π * f * t + Ф)
Das Informationssignal, auch als Basisbandsignal bekannt, verändert sich zeitlich viel langsamer als das HF-Signal. Um die Wirkung der Modulation zu erkennen, muss man daher die Hüllkurve des HF-Signals über einen längeren Zeitraum beobachten, wie unten gezeigt.
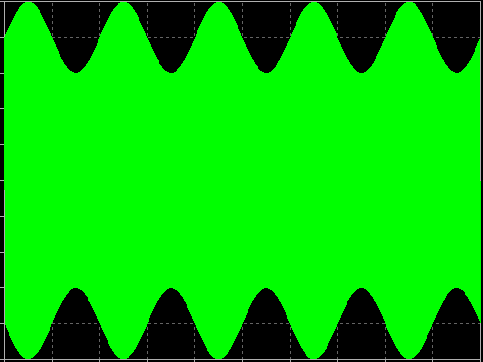
In diesem Fall ist das A(t)-Signal eine Sinuskurve. Die Abbildung zeigt, wie die Amplitude des HF-Signals dem sinusförmigen A(t)-Basisbandsignal folgt.
Sie können dies erweitern, indem Sie erkennen, dass andere Eigenschaften des HF-Trägers durch ein Basisbandsignal in Abhängigkeit von der Zeit verändert oder moduliert werden können. Wenn die Frequenz durch ein Basisbandsignal moduliert wird, spricht man von Frequenzmodulation (FM). Wenn die Phase moduliert wird, spricht man von Phasenmodulation (PM). Also:
- A(t) ist, wenn die Amplitude gegen die Zeit verändert wird
- f(t) ist, wenn die Frequenz gegen die Zeit verändert wird
- Ф(t) ist, wenn die Phase gegen die Zeit verändert wird.
Behalten Sie das grundlegende Konzept der Modulation im Hinterkopf, wenn wir das Konzept der Quadratursignale einbeziehen…
Quadratursignalkonzepte
Wenn die Phasendifferenz Ф zwischen zwei Sinuskurven 90 Grad (oder π /2 Radiant) beträgt, dann sagt man, dass diese beiden Signale in Quadratur sind. Ein Beispiel hierfür sind die Sinuswelle und die Kosinuswelle.
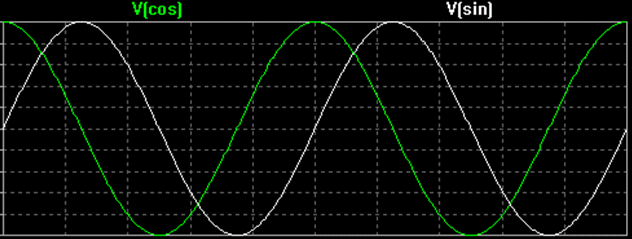
Nach der Konvention ist die Kosinuswelle die In-Phase-Komponente und die Sinuswelle die Quadratur-Komponente. Der Großbuchstabe I steht für die Amplitude des gleichphasigen Signals und der Großbuchstabe Q für die Amplitude des Quadratursignals.
Verwendung von Quadratursignalen zur Modulation
Interessante Dinge passieren, wenn man Quadratursignale zusammenzählt.
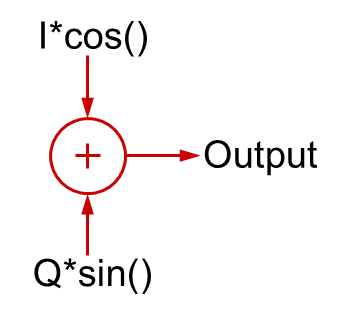
Wenn I=1 und Q=0, dann hätte man einfach die Kosinuswelle (Phase gleich 0). Wenn I=0 und Q=1 wäre, hätte man die Sinuswelle, also das um 90 Grad verschobene Signal.
Wenn sowohl I als auch Q gleich 1 wären, dann wäre die Summe ein neues Signal, das unten grafisch dargestellt ist.
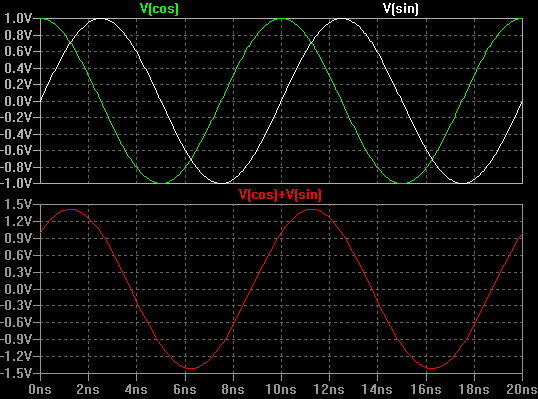
Beachte, dass die Addition dieser beiden Quadratursignale mit gleicher Amplitude eine neue Sinuswelle ergibt, die um 45 Grad phasenverschoben ist.
Sie sehen jetzt, dass die Amplitude und die Phase der Summe der Quadratursignale eine Funktion des Wertes von I und Q ist. Daher können Sie modulierte HF-Signale erzeugen, indem Sie die Werte von I und Q in Abhängigkeit von der Zeit variieren. Sehen wir uns ein paar Beispiele an:
Beispiele für digitale HF-Modulation
Wenn Q=0 ist und I im Laufe der Zeit zwischen +1 und -1 verändert wird, entsteht ein binäres phasenumgetastetes HF-Signal (BPSK):
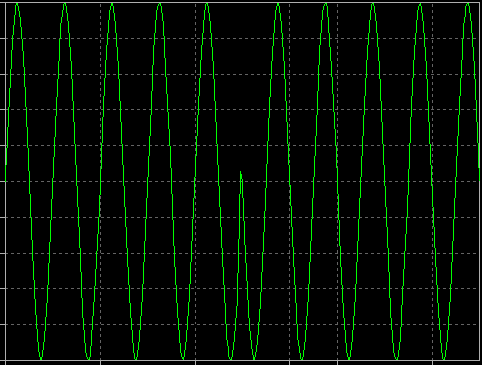
Das I(t)-Signal könnte ein einfacher digitaler Bitstrom sein. Wenn man dieses Signal die Verstärkung der HF-Sinuskurve zwischen +1 und -1 steuern lässt, hat man ein BPSK-Signal erzeugt.
Gehen wir noch einen Schritt weiter… Wenn zwei digitale Bits verwendet werden, um die I- und Q-Werte zwischen +1 und -1 über die Zeit zu steuern, dann kann die resultierende Summe der Quadratursignale eine von vier verschiedenen Phasen sein:
- I=+1 & Q=+1 ergibt eine Phase von 45 Grad
- I=-1 & Q=+1 ergibt eine Phase von 135 Grad
- I=-1 & Q=-1 ergibt eine Phase von 225 Grad
- I=+1 & Q=-1 ergibt eine Phase von 315 Grad
Dies wird als Quadraturphasenumtastungsmodulation (QPSK) bezeichnet. Dies sind zwei Beispiele für die Quadratur-Amplituden-Modulation (QAM). Die verschiedenen Modulationszustände für QAM werden häufig in einem Konstellationsdiagramm dargestellt. Ein Konstellationsdiagramm ist einfach ein Phasendiagramm, das die Amplitude und Phase eines Signals als Polardiagramm darstellt.
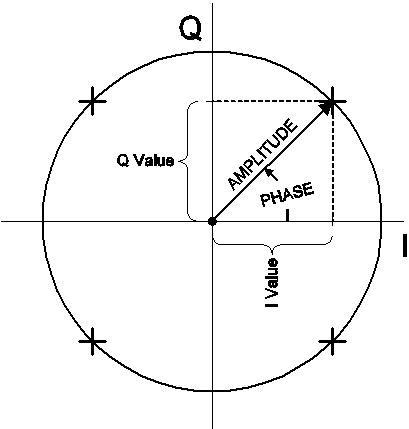
Die Länge des Vektors vom Ursprung aus stellt die Signalgröße dar, und der Winkel, den der Vektor mit der horizontalen Achse bildet, stellt die Phase dar. Die vier „Zustände“ für das oben beschriebene QPSK-Signal sind im Diagramm durch die vier „+“-Symbole dargestellt. Sie werden auch feststellen, dass die horizontale Achse mit „I“ und die vertikale Achse mit „Q“ beschriftet ist – denn diese stellen die I- und Q-Komponentenwerte dar, die mit dem Signal verbunden sind.
Komplexere QAM-Modulationen, wie 16QAM, haben einfach mehr Zustände. Bei 16QAM können die I- und Q-Werte jeweils einen von vier diskreten Werten annehmen, was zu 16 möglichen Kombinationen führt. Daraus ergeben sich 16 Amplituden- und Phasenkombinationen für das HF-Signal.
Quadratursignale überall
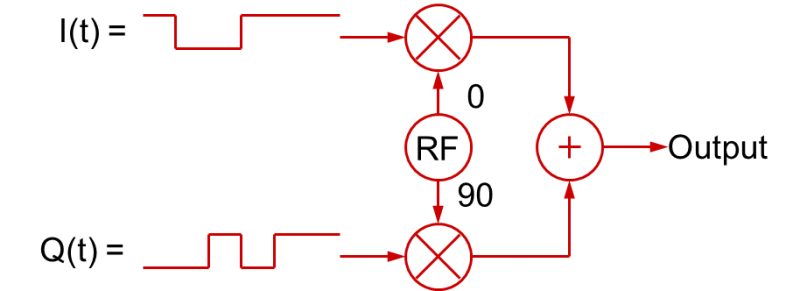
Die Verwendung von I- und Q-Signalen, die im Laufe der Zeit variieren, um modulierte HF-Signale zu erzeugen, ist nicht auf digitale Basisbandsignale beschränkt. Die I(t)- und Q(t)-Basisbandsignale können auch analoge Basisbandsignale sein. Tatsächlich werden bei den meisten „digital“ modulierten HF-Anwendungen wie QPSK oder nQAM die Basisbandsignale gefiltert, um die Übergänge zu verlangsamen. Dies geschieht, um die resultierende Bandbreite des modulierten HF-Signals zu begrenzen (schnelle digitale Anstiegs-/Abfallzeiten beanspruchen viel Bandbreite!). Diese gefilterten digitalen Signale sind eigentlich analoge Signale! In einem allgemeineren Sinne kann der Prozess der Quadraturmodulation wie in dieser Abbildung dargestellt werden:
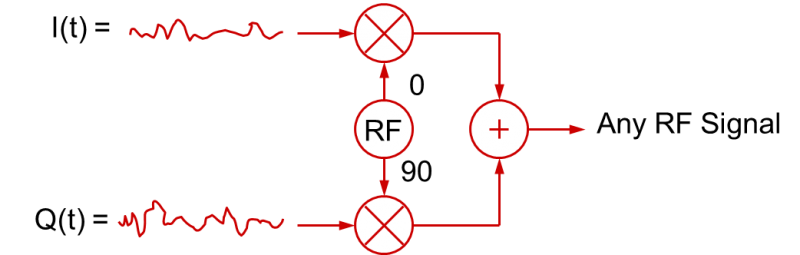
Die allgemeine Schlussfolgerung, die man daraus ziehen kann, ist, dass ein HF-Signal mit jeder Art von Modulation mit den entsprechenden I(t)- und Q(t)-Basisbandsignalen erzeugt werden kann (die wiederum die Amplituden der Kosinus- und Sinuswellen variieren, die zusammen summiert werden).
Natürlich funktioniert derselbe Prozess in umgekehrter Richtung, um ein HF-Signal zu demodulieren. Durch Mischen eines HF-Signals mit LO-Signalen (Lokaloszillator) in Quadratur können I(t)- und Q(t)-Basisbandsignale erzeugt werden.
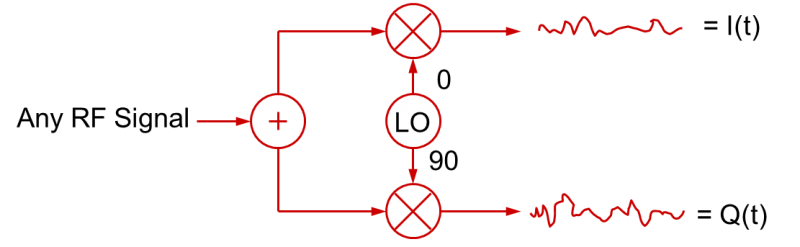
Dies ist die grundlegende Basis für die meisten modernen HF-Signalerzeugungs- und Modulationsverfahren sowie für die Demodulation und Vektorsignalanalyse.
Software Defined Radio (SDR)-Systeme nutzen diese Konzepte ausgiebig, da die Basisband I & Q-Signale oft als diskrete zeitlich abgetastete Daten dargestellt werden. Daher kann die digitale Signalverarbeitung (DSP) verwendet werden, um die Sender- und Empfängereigenschaften einschließlich Filterung, Modulation und Demodulation, AGC usw. buchstäblich zu definieren. SDR-Empfänger verfügen oft über eine Basisbandbreite von einigen hundert kHz oder mehr, wodurch sie eine Vielzahl von Funktionen ausführen können, einschließlich „breiter“ Bandscope- und Spektrogramm-Funktionen, sowie die Möglichkeit, mehrere Signale unterschiedlicher Art gleichzeitig zu überwachen und zu demodulieren.
Vektorsignalgeneratoren verfügen über einen Quadraturmodulator, der I(t)- und Q(t)-Signale akzeptiert, die er dann zur Amplitudenmodulation eines Paares von Quadratursinuskurven verwendet, die dann summiert werden, um den modulierten HF-Ausgang zu erzeugen. Viele Vektorsignalgeneratoren verfügen im Allgemeinen über Anschlussbuchsen, an die Sie Ihre eigenen IQ-Signale anschließen können. Viele enthalten einen internen Basisband Arbitrary Waveform Generator (AWG), um die Basisband-IQ-Signale zu erzeugen.
Moderne Vektorsignalanalysatoren haben typischerweise Bandbreiten von 25, 40, 110 MHz oder mehr. Sie wandeln die eingehenden HF-Signale in ihre I- und Q-Komponenten um. Die gesamte Analyse (Spektralanalyse im Zeitverlauf, Demodulation, Impulsanalyse usw.) ist einfach eine andere mathematische Verarbeitung der gleichen IQ-Daten. Echtzeit-Signalanalysatoren wie die RSA5000- und RSA6000-Serien von Tektronix verfügen über die zusätzliche Fähigkeit, die „Live“-IQ-Datenströme zu übernehmen und eine Echtzeitverarbeitung der Daten durchzuführen. Dies ermöglicht z. B. die Visualisierung des Live-Spektrums eines HF-Signals sowie die Auslösung von transienten Ereignissen, die nur im Frequenzbereich sichtbar sind.
Siehe die neuesten Spektrumanalysatorangebote von Tektronix.