Die Röntgenbeugung ist ein gängiges Verfahren zur Materialcharakterisierung, das die Identifizierung von Kristallorientierungen und interatomaren Abständen ermöglicht. Röntgenstrahlen werden dafür verwendet, weil die Wellenlänge auf der gleichen Längenskala liegt wie die interatomaren Abstände und die Gitterparameterwerte.
Was passiert da?
Ein Röntgenstrahl wird in einer Vakuumröhre erzeugt, indem ein Wolframfaden über seine Arbeitsfunktion hinaus erhitzt wird, um Elektronen auszustoßen. Die Vakuumbedingungen sind notwendig, um die mittlere freie Weglänge der Elektronen zu erhöhen. Die Elektronen werden mit einer Energie in der Größenordnung von 25 keV auf eine Kupferkathode beschleunigt. Elektronenkollisionen mit der Kupferkathode führen zu Ionisationen in der inneren Schale, wobei Röntgenstrahlung entsteht, da Elektronen mit höherer Energie in den Hohlraum mit niedrigerer Energie fallen. Elektronen aus verschiedenen höheren Energieniveaus fallen ab und erzeugen elektromagnetische Wellen unterschiedlicher Energie. Auf diese Weise werden Röntgenstrahlen mit verschiedenen Wellenlängen (vom Typ K-beta und K-alpha) erzeugt. Für die Röntgenbeugung ist es ideal, wenn monochromatisches Licht mit der Probe interagiert, daher werden die K-beta-Röntgenstrahlen mit einer Nickelplatte herausgefiltert. Obwohl es tatsächlich zwei assoziierte K-alpha-Energien gibt, sind die Energien so ähnlich, dass sie das Gesamtpeakprofil nicht wesentlich beeinflussen. Die Röntgenstrahlen durchlaufen einen Kollimator, um die Strahlbreite einzustellen.
Ein wenig Hintergrundwissen zum Bragg’schen Gesetz
Das Bragg’sche Gesetz beschreibt die Beziehung für konstruktive Interferenz, bei der Röntgenstrahlen der Wellenlänge λ, die unter dem Winkel θ auf das Material einfallen, von Kristallebenen gebeugt werden, die durch den Abstand d getrennt sind, wobei n eine ganze Zahl darstellt.
Wie unten gezeigt, bewirkt eine Phasenverschiebung der Welle je nach dem Winkel 2θ entweder konstruktive Interferenz, wie links dargestellt, oder destruktive Interferenz, wie rechts dargestellt.
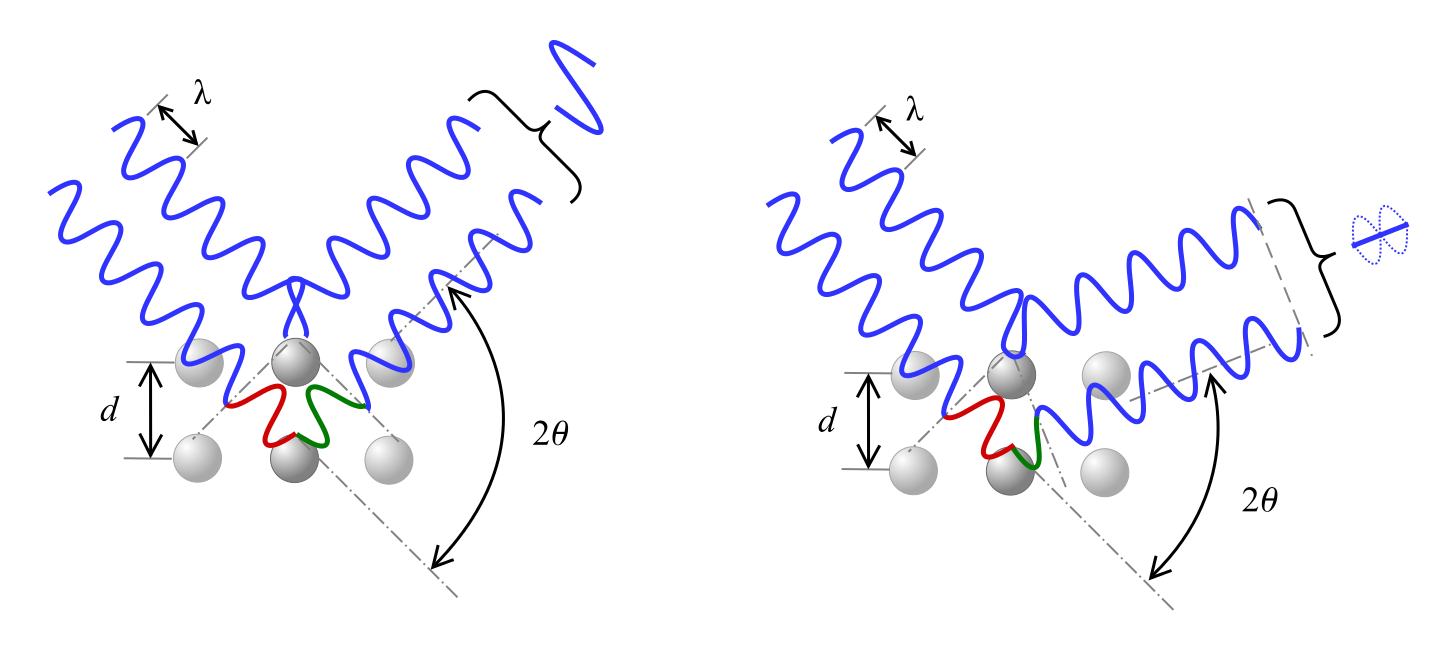
Gleichungen zur Interpretation von XRD-Ergebnissen
Der Zähler, der unten in einem Schema eines Röntgendiffraktometers zu sehen ist, wird über einen Bereich von 2θ-Werten gedreht und zeichnet die Intensität des vom Kristall reflektierten Röntgensignals an jeder Position auf. Diese als Funktion von 2θ gemessene Intensität wird zur Erstellung eines Spitzenprofils verwendet.
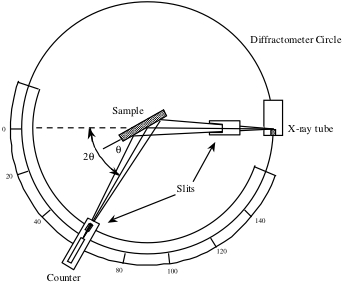
Bei Winkeln, die die Bragg-Bedingung erfüllen, wird aufgrund der konstruktiven Interferenz eine Spitze im Röntgensignal beobachtet. Diese Peaks werden dann zur Identifizierung der Kristallrichtungen und zur Berechnung der Gitterparameter verwendet. Für kubische Systeme kann der Interplanarabstand d mit der folgenden, aus der Kristallgeometrie abgeleiteten Gleichung berechnet werden, wobei a der Gitterparameter und h, k und l die Miller-Indizes sind.
Die Kombination des Braggschen Gesetzes und des Interplanarabstands ergibt die folgende Gleichung.
Hier haben wir alle Konstanten auf die linke Seite der Gleichung verschoben, so dass wir die Verhältnisse der sin2(θ)-Werte und Miller-Indizes zwischen verschiedenen Peaks vergleichen können.
Wenn die einfallende elektromagnetische Welle auf das Probenmaterial auftrifft, werden die im Material befindlichen Elektronen in ein Schwingungsmuster versetzt, das neue Röntgenstrahlen erzeugt und die einfallenden Lichtwellen effektiv streut. Es gibt zwei Arten von Streuung: die kohärente oder elastische Streuung, bei der fest gebundene, oszillierende Elektronen Röntgenstrahlen derselben Wellenlänge streuen, und die inkohärente Streuung, die auftritt, wenn lose gebundene Elektronen in Schwingung versetzt werden und Röntgenstrahlen unterschiedlicher Energie erzeugen. Bei der Röntgenbeugung wird die Intensität der kohärent gestreuten Röntgenstrahlung gemessen, die dort ihren Höhepunkt erreicht, wo die Wellen konstruktiv interferieren. Der atomare Streufaktor kann definiert werden als das Verhältnis der Amplitude der von einem Atom gestreuten Welle geteilt durch die Amplitude der von einem einzelnen Elektron gestreuten Welle. Dieses Verhältnis beschreibt im Wesentlichen die Streueffizienz eines Atoms für eine bestimmte Richtung.
Beispiel für XRD-Daten
Hier sind die Daten aus einem Experiment, das ich während meines Grundstudiums im Labor durchgeführt habe, um ein unbekanntes Metall anhand seiner Kristallstruktur zu identifizieren.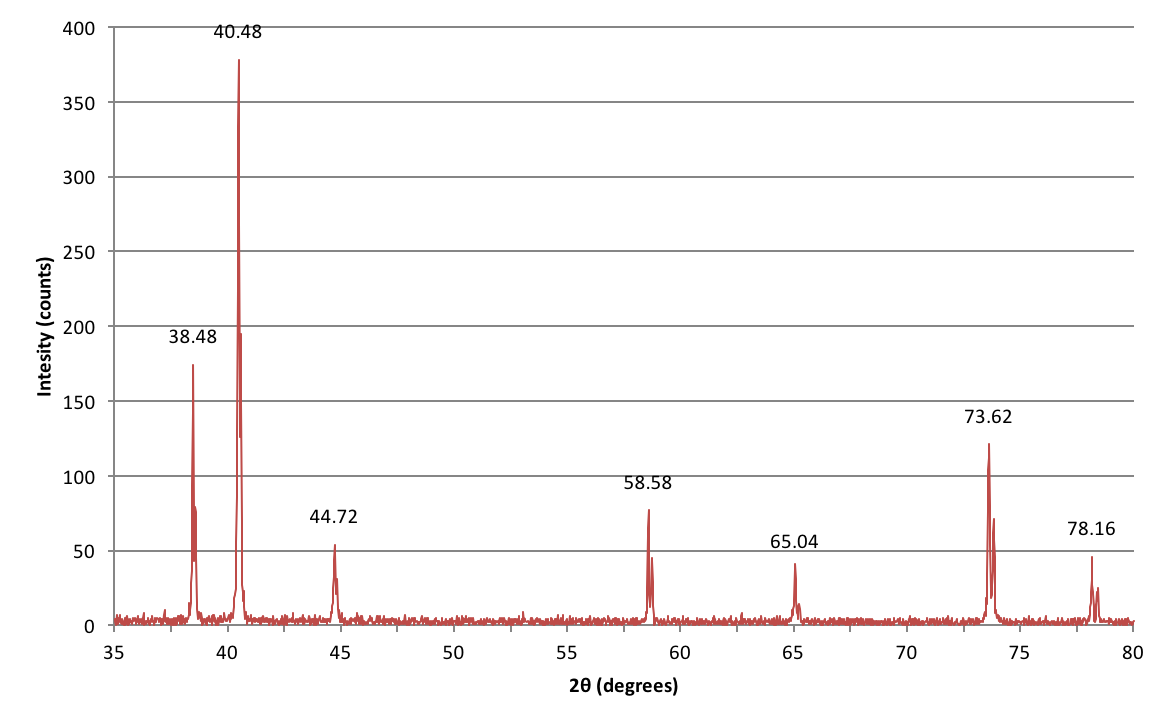
Wie interpretiere ich diese Peaks?
| Kristallstruktur | Bedingungen |
|---|---|
| Einfach kubisch | alle h, k, l-Werte |
| Körperzentrierter Kubus | h+k+l müssen gerade sein |
| Flächenzentrierter Kubus | h, k und l müssen alle ungerade oder alle gerade sein |
Die Strukturfaktoren berücksichtigen die Fälle, in denen eine Ebene auf halbem Weg zwischen zwei benachbarten Ebenen liegt und destruktive Interferenzen hervorruft. Diese Faktoren führen zu einer Reihe von Regeln für verschiedene Kristallstrukturgeometrien, die bestimmen, wann konstruktive Interferenz auftreten kann. In der obigen Tabelle sind die Miller-Index-Parameter aufgeführt, bei denen konstruktive Interferenz auftritt. Eine ausführlichere Tabelle finden Sie weiter unten. Durch den Vergleich der Verhältnisse von sin2θ (in der zweiten Tabelle als $Q^2$ bezeichnet) für verschiedene Beugungspeaks lassen sich die Kristallstruktur und die Miller-Indizes bestimmen.
| Kristallebene (hkl) | $Q^2$ | Raumgitter, von denen Reflexionen möglich sind | ||||
|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||
| 110 | 2 | SC | BCC | |||
| 111 | 3 | SC | FCC | DC | ||
| 200 | 4 | SC | BCC | FCC | ||
| 210 | 5 | SC | ||||
| 211 | 6 | SC | BCC | |||
| – | 7 | |||||
| 220 | 8 | SC | BCC | FCC | DC | |
| 300, 221 | 9 | SC | ||||
| 310 | 10 | SC | BCC | |||
| 311 | 11 | SC | FCC | DC | ||
| 222 | 12 | SC | BCC | FCC | ||
| 320 | 13 | SC | ||||
| 321 | 14 | SC | BCC | |||
| – | 15 | |||||
| 400 | 16 | SC | BCC | FCC | DC | |
X-Strahlenbeugung hat eine breite Palette von Anwendungen für die Charakterisierung von Materialien. Sie kann als experimentelle Methode verwendet werden, um das Volumen einer Einheitszelle für theoretische Dichteberechnungen zu bestimmen. Wenn das Material unter Eigenspannung steht, weist das verzerrte Gitter außerdem eine Reihe von d-Abständen auf, die das Bragg’sche Gesetz erfüllen, was zu viel breiteren Beugungsspitzen führt. Die Breite des Beugungspeaks kann auch zur Bestimmung der Partikelgröße verwendet werden.