Wenn wir über Modellvorhersagen sprechen, ist es wichtig, die Vorhersagefehler (Bias und Varianz) zu verstehen. Es besteht ein Kompromiss zwischen der Fähigkeit eines Modells, Verzerrungen und Varianz zu minimieren. Wenn wir diese Fehler richtig verstehen, können wir nicht nur genaue Modelle erstellen, sondern auch den Fehler der Über- und Unteranpassung vermeiden.
Beginnen wir also mit den Grundlagen und sehen wir, wie sie unsere Modelle für maschinelles Lernen beeinflussen.
Was ist Bias?
Bias ist die Differenz zwischen der durchschnittlichen Vorhersage unseres Modells und dem richtigen Wert, den wir vorherzusagen versuchen. Ein Modell mit hohem Bias schenkt den Trainingsdaten sehr wenig Aufmerksamkeit und vereinfacht das Modell zu sehr. Es führt immer zu hohen Fehlern bei den Trainings- und Testdaten.
Was ist Varianz?
Varianz ist die Variabilität der Modellvorhersage für einen bestimmten Datenpunkt oder einen Wert, der uns die Streuung unserer Daten zeigt. Ein Modell mit hoher Varianz schenkt den Trainingsdaten große Aufmerksamkeit und verallgemeinert nicht auf Daten, die es noch nicht gesehen hat. Infolgedessen schneiden solche Modelle bei den Trainingsdaten sehr gut ab, weisen aber bei den Testdaten hohe Fehlerquoten auf.
Mathematisch
Nennen wir die Variable, die wir vorhersagen wollen, Y und die anderen Kovariaten X. Wir nehmen an, dass es eine Beziehung zwischen den beiden gibt, so dass
Y=f(X) + e
wobei e der Fehlerterm ist und normalverteilt ist mit einem Mittelwert von 0.
Wir werden ein Modell f^(X) von f(X) mit Hilfe der linearen Regression oder einer anderen Modellierungstechnik erstellen.
Der erwartete quadratische Fehler an einem Punkt x ist also
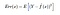
Der Err(x) kann weiter zerlegt werden als

Err(x) ist die Summe von Bias², Varianz und dem irreduziblen Fehler.
Der irreduzible Fehler ist der Fehler, der nicht durch die Erstellung guter Modelle reduziert werden kann. Er ist ein Maß für die Menge des Rauschens in unseren Daten. Hier ist es wichtig zu verstehen, dass, egal wie gut wir unser Modell machen, unsere Daten eine gewisse Menge an Rauschen oder irreduziblem Fehler haben werden, die nicht entfernt werden können.
Vorspannung und Varianz unter Verwendung des Bulls-Eye-Diagramms

In dem obigen Diagramm ist die Mitte des Ziels ein Modell, das perfekt korrekte Werte vorhersagt. Je weiter wir uns von der Zielscheibe entfernen, desto schlechter werden unsere Vorhersagen. Wir können den Prozess der Modellbildung wiederholen, um einzelne Treffer auf dem Ziel zu erzielen.
Beim überwachten Lernen kommt es zu einer Unteranpassung, wenn ein Modell nicht in der Lage ist, das zugrunde liegende Muster der Daten zu erfassen. Diese Modelle haben in der Regel eine hohe Verzerrung und eine geringe Varianz. Das passiert, wenn wir nur eine sehr geringe Menge an Daten haben, um ein genaues Modell zu erstellen, oder wenn wir versuchen, ein lineares Modell mit nichtlinearen Daten zu erstellen. Außerdem sind diese Art von Modellen sehr einfach, um die komplexen Muster in den Daten zu erfassen, wie z. B. die lineare und logistische Regression.
Beim überwachten Lernen kommt es zu einer Überanpassung, wenn unser Modell das Rauschen zusammen mit dem zugrunde liegenden Muster in den Daten erfasst. Dies geschieht, wenn wir unser Modell häufig mit verrauschten Datensätzen trainieren. Diese Modelle haben eine geringe Verzerrung und eine hohe Varianz. Diese Modelle sind sehr komplex, wie z.B. Entscheidungsbäume, die anfällig für Overfitting sind.

Warum gibt es einen Bias-Varianz-Kompromiss?
Wenn unser Modell zu einfach ist und nur wenige Parameter hat, kann es einen hohen Bias und eine geringe Varianz haben. Wenn unser Modell hingegen eine große Anzahl von Parametern hat, dann wird es eine hohe Varianz und eine geringe Verzerrung aufweisen. Wir müssen also das richtige Gleichgewicht finden, ohne die Daten zu sehr oder zu wenig anzupassen.
Dieser Kompromiss bei der Komplexität ist der Grund, warum es einen Kompromiss zwischen Verzerrung und Varianz gibt. Ein Algorithmus kann nicht gleichzeitig komplexer und weniger komplex sein.
Gesamtfehler
Um ein gutes Modell zu erstellen, müssen wir ein gutes Gleichgewicht zwischen Bias und Varianz finden, so dass der Gesamtfehler minimiert wird.


Ein optimales Gleichgewicht zwischen Verzerrung und Varianz würde das Modell weder über- noch unteranpassen.
Deshalb ist das Verständnis von Bias und Varianz von entscheidender Bedeutung, um das Verhalten von Vorhersagemodellen zu verstehen.
Danke fürs Lesen!