Einführung
In der Informatik ist ein gerichteter azyklischer Graph (DAG) ein gerichteter Graph ohne Zyklen. In diesem Tutorium zeigen wir, wie man eine topologische Sortierung auf einem DAG in linearer Zeit durchführt.
Topologische Sortierung
In vielen Anwendungen verwenden wir gerichtete azyklische Graphen, um Prioritäten zwischen Ereignissen anzugeben. Zum Beispiel gibt es bei einem Planungsproblem eine Menge von Aufgaben und eine Menge von Beschränkungen, die die Reihenfolge dieser Aufgaben angeben. Wir können ein DAG konstruieren, um Aufgaben darzustellen. Die gerichteten Kanten des DAG stellen die Reihenfolge der Aufgaben dar.
Betrachten wir ein Problem, bei dem es darum geht, wie sich eine Person für einen formellen Anlass anziehen könnte. Man muss mehrere Kleidungsstücke anziehen, z. B. Socken, Hosen, Schuhe usw. Einige Kleidungsstücke müssen vor den anderen angezogen werden. Zum Beispiel müssen wir die Socken vor den Schuhen anziehen. Einige Kleidungsstücke können in beliebiger Reihenfolge angezogen werden, z. B. Socken und Hosen. Wir können ein DAG verwenden, um dieses Problem zu veranschaulichen:
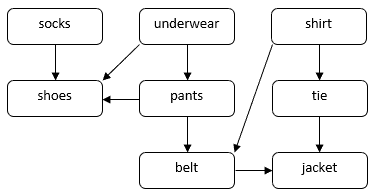
In diesem DAG entsprechen die Knoten den Kleidungsstücken. Eine direkte Kante 
in der DAG zeigt an, dass wir das Kleidungsstück 
vor dem Kleidungsstück 
anziehen müssen. Unsere Aufgabe ist es, eine Reihenfolge für das Anlegen aller Kleidungsstücke zu finden und dabei die Abhängigkeitsbedingungen zu beachten. Zum Beispiel können wir die Kleidungsstücke in der folgenden Reihenfolge anziehen:
Eine topologische Sortierung einer DAG 
ist eine lineare Anordnung aller ihrer Eckpunkte, so dass, wenn eine Kante enthält, in der Anordnung vor erscheint. Für ein DAG können wir eine topologische Sortierung konstruieren, deren Laufzeit linear zur Anzahl der Knoten plus der Anzahl der Kanten ist, also 
.
Kahns Algorithmus
In einem DAG hat jeder Pfad zwischen zwei Knoten eine endliche Länge, da der Graph keinen Zyklus enthält. Sei 
der längste Weg von (Quellknoten) nach (Zielknoten). Da der längste Pfad ist, kann es keine eingehende Kante zu geben. Daher enthält eine DAG mindestens einen Knoten, der keine eingehende Kante hat.
3.1. Kahns Algorithmus
In Kahns Algorithmus konstruieren wir eine topologische Sortierung auf einer DAG, indem wir Knoten finden, die keine eingehenden Kanten haben:
In diesem Algorithmus berechnen wir zuerst die In-Grad-Werte für alle Knoten.
Dann beginnen wir mit einem Knoten, dessen In-Grad 0 ist, und setzen ihn an das Ende der Ausgabeliste. Sobald wir einen Scheitelpunkt ausgewählt haben, aktualisieren wir die In-Grad-Werte seiner benachbarten Scheitelpunkte, da der Scheitelpunkt und seine Außenkanten aus dem Graphen entfernt werden.
Wir können den obigen Vorgang wiederholen, bis wir alle Scheitelpunkte ausgewählt haben. Die Ausgabeliste ist dann eine topologische Sortierung des Graphen.
3.2. Zeitkomplexität
Um die in-degrees aller Scheitelpunkte zu berechnen, müssen wir alle Scheitelpunkte und Kanten von besuchen. Daher beträgt die Laufzeit für In-degree-Berechnungen. Um zu vermeiden, dass diese Werte erneut berechnet werden müssen, können wir ein Array verwenden, um die In-Grad-Werte dieser Scheitelpunkte zu speichern. Innerhalb der while-Schleife müssen wir auch alle Knoten und Kanten besuchen. Daher beträgt die Gesamtlaufzeit .
Depth First Search
Wir können auch einen Depth First Search (DFS) Algorithmus verwenden, um die topologische Sortierung zu erstellen.
4.1. Graph DFS mit Rekursion
Bevor wir den Aspekt der topologischen Sortierung mit DFS in Angriff nehmen, wollen wir zunächst einen rekursiven Standard-DFS-Algorithmus zur Durchquerung von Graphen betrachten:
Im Standard-DFS-Algorithmus beginnen wir mit einem zufälligen Knoten in und markieren diesen Knoten als besucht. Dann rufen wir rekursiv die Funktion dfsRecursive auf, um alle nicht besuchten benachbarten Scheitelpunkte zu besuchen. Auf diese Weise können wir alle Scheitelpunkte von in Zeit besuchen.
Da wir jedoch jeden Scheitelpunkt sofort in die Liste aufnehmen, wenn wir ihn besuchen, und da wir an jedem beliebigen Scheitelpunkt beginnen können, kann der Standard-DFS-Algorithmus nicht garantieren, dass er eine topologisch sortierte Liste erzeugt.
Lassen Sie uns sehen, was wir tun müssen, um diesen Mangel zu beheben.
4.2. DFS-basierter topologischer Sortieralgorithmus
Wir können den DFS-Algorithmus modifizieren, um eine topologische Sortierung einer DAG zu erzeugen. Während der DFS-Traversierung, nachdem alle Nachbarn eines Scheitelpunkts besucht wurden, setzen wir ihn an den Anfang der Ergebnisliste 
. Auf diese Weise können wir sicherstellen, dass vor allen seinen Nachbarn in der sortierten Liste erscheint:
Dieser Algorithmus ähnelt dem Standard-DFS-Algorithmus. Obwohl wir immer noch mit einem zufälligen Knoten beginnen, setzen wir den Knoten nicht sofort in die Liste, wenn wir ihn besuchen. Stattdessen werden zunächst alle seine Nachbarn rekursiv besucht und der Knoten dann an den Anfang der Liste gesetzt. Wenn also eine Kante enthält, erscheint vor in der Liste.
Die Gesamtlaufzeit beträgt ebenfalls , da sie die gleiche Zeitkomplexität wie der DFS-Algorithmus hat.
Schlussfolgerung
In diesem Artikel haben wir ein Beispiel für topologisches Sortieren auf einem DAG gezeigt. Außerdem haben wir zwei Algorithmen diskutiert, die eine topologische Sortierung in Zeit durchführen können.
Die Java-Implementierung des DFS-basierten topologischen Sortieralgorithmus ist in unserem Artikel über Depth First Search in Java verfügbar.