Probability > Posterior Probability & the Posterior Distribution
What is Posterior Probability?
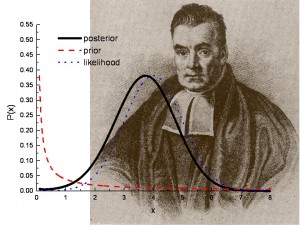
Posterior Probabilities are used in Bayesian hypothesis testing. Bild: Los Alamos National Lab.
Posterior-Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, nachdem alle Beweise oder Hintergrundinformationen berücksichtigt wurden. Sie ist eng verwandt mit der vorherigen Wahrscheinlichkeit, die die Wahrscheinlichkeit ist, dass ein Ereignis eintritt, bevor man neue Beweise berücksichtigt hat. Man kann sich die posteriore Wahrscheinlichkeit als eine Anpassung der prioren Wahrscheinlichkeit vorstellen:
Zum Beispiel deuten historische Daten darauf hin, dass etwa 60 % der Studenten, die ein College beginnen, es innerhalb von 6 Jahren abschließen werden. Dies ist die vorherige Wahrscheinlichkeit. Sie glauben jedoch, dass diese Zahl in Wirklichkeit viel niedriger ist, und machen sich auf den Weg, um neue Daten zu sammeln. Die gesammelten Daten deuten darauf hin, dass die tatsächliche Zahl eher bei 50 % liegt; dies ist die posteriore Wahrscheinlichkeit.
Herkunft der Begriffe
Die Begriffe posterior und prior kommen vom lateinischen a priori. Die Definition von „a priori“ lautet:
„…in Bezug auf das, was durch ein Verständnis dessen, wie bestimmte Dinge funktionieren, und nicht durch Beobachtung bekannt werden kann“ ~ Miriam Webster.
Das Gegenteil von „a priori“ ist a posteriori, definiert als:
„… in Bezug auf das, was durch Beobachtung und nicht durch ein Verständnis dafür, wie bestimmte Dinge funktionieren, bekannt werden kann“ ~ Miriam Webster.
Was ist eine Posterior-Verteilung?
Die Posterior-Verteilung ist eine Möglichkeit, zusammenzufassen, was wir über ungewisse Größen in der Bayes’schen Analyse wissen. Sie ist eine Kombination aus der Priorverteilung und der Likelihood-Funktion, die angibt, welche Informationen in den beobachteten Daten (den „neuen Beweisen“) enthalten sind. Mit anderen Worten: Die Posterior-Verteilung fasst zusammen, was Sie wissen, nachdem die Daten beobachtet wurden. Die Zusammenfassung der Evidenz aus den neuen Beobachtungen ist die Likelihood-Funktion.
Posterior-Verteilungen sind in der Bayesschen Analyse von entscheidender Bedeutung. Sie sind in vielerlei Hinsicht das Ziel der Analyse und können Ihnen:
- Intervallschätzungen für Parameter,
- Punktschätzungen für Parameter,
- Vorhersage-Inferenz für zukünftige Daten,
- wahrscheinlichkeitstheoretische Bewertungen für Ihre Hypothese liefern.
Stephanie Glen. „Posterior Probability & the Posterior Distribution“ From StatisticsHowTo.com: Elementare Statistik für den Rest von uns! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf dem Gebiet erhalten. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!