Zurück zum Lektionen-Index | Die Lektionen der Reihe nach machen | Druckfreundliche Seite
Matrix-Zeilen-Operationen (Seite 1 von 2)
„Operationen“ ist Mathematiker-Fachsprache für „Verfahren“. Die vier „Grundoperationen“ bei Zahlen sind Addition, Subtraktion, Multiplikation und Division. Für Matrizen gibt es drei grundlegende Zeilenoperationen, d.h. es gibt drei Verfahren, die man mit den Zeilen einer Matrix durchführen kann.
Die erste Operation ist die Zeilenverschiebung. Zum Beispiel, wenn die Matrix:

…können Sie die Zeilen vertauschen, um die Matrix in eine schönere Zeilenanordnung zu bringen, z.B. so:
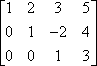
Das Vertauschen von Zeilen wird oft durch das Zeichnen von Pfeilen angezeigt, z.B. so:

Wenn Sie Zeilen vertauschen, achten Sie darauf, dass Sie die Einträge korrekt kopieren.
Die zweite Operation ist die Zeilenmultiplikation. Bei der folgenden Matrix zum Beispiel:

…kann man die erste Zeile mit -1 multiplizieren, um einen positiven führenden Wert in der ersten Zeile zu erhalten:
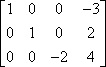
Diese Zeilenmultiplikation wird oft durch einen Pfeil mit der Multiplikation oben drauf angezeigt, etwa so:
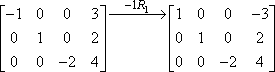
Das „-1R1“ zeigt die eigentliche Operation an. Die „-1“ besagt, dass wir mit minus eins multipliziert haben; die „R1“ besagt, dass wir mit der ersten Zeile gearbeitet haben. Beachten Sie, dass die zweite und dritte Zeile unverändert in die zweite Matrix kopiert wurden. Die Multiplikation galt nur für die erste Zeile, so dass die Einträge für die anderen beiden Zeilen einfach unverändert übernommen wurden.
Sie können mit allem multiplizieren, was Sie wollen. Um zum Beispiel eine führende 1 in der dritten Zeile der vorherigen Matrix zu erhalten, können Sie die dritte Zeile mit einer negativen Hälfte multiplizieren:

Da Sie nichts mit der ersten und zweiten Zeile gemacht haben, wurden diese Einträge einfach unverändert in die neue Matrix übernommen.
Sie können mehr als eine Zeilenmultiplikation im selben Schritt durchführen, so dass Sie die beiden obigen Schritte in nur einem Schritt hätten durchführen können, etwa so:
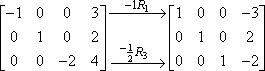
Es ist eine gute Idee, eine Form der Notation zu verwenden (wie die Pfeile und tiefgestellten Indizes oben), damit Sie den Überblick über Ihre Arbeit behalten können. Matrizen sind sehr unübersichtlich, vor allem, wenn Sie sie von Hand erstellen, und Notizen können es Ihnen erleichtern, Ihre Arbeit später zu überprüfen. Es wird auch deinen Lehrer beeindrucken.
Die letzte Zeilenoperation ist die Zeilenaddition. Die Zeilenaddition ähnelt der „Additionsmethode“ zum Lösen von linearen Gleichungssystemen. Angenommen, du hast das folgende Gleichungssystem:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Anmerkung
Du könntest dieses System lösen, indem du die Spalten nach unten addierst, um 4y = 4 zu erhalten:
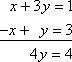
Sie können etwas Ähnliches mit Matrizen machen.Bei der folgenden Matrix zum Beispiel:

…kann man die zweite Zeile „reduzieren“ (mehr führende Nullen erhalten), indem man die erste Zeile hinzufügt (das allgemeine Ziel bei Matrizen in diesem Stadium ist es, eine „1“ – oder „0’s“ und dann eine „1“ – am Anfang jeder Matrixzeile zu erhalten). Beim Reduzieren des linearen Zweigleichungssystems durch Addieren haben Sie eine „Gleichheits“-Leiste quer über den Boden gezeichnet und nach unten addiert. Wenn du die Addition bei einer Matrix anwendest, musst du dir ein Stück Schmierpapier nehmen, weil du nicht versuchen willst, die Arbeit innerhalb der Matrix zu erledigen. Addiere also die beiden Zeilen auf deinem Schmierpapier:
|
Kratzarbeit – |
|
Dies ist deine neue zweite Zeile; du wirst sie anstelle der alten zweiten Zeile schreiben. Das Ergebnis sieht wie folgt aus:
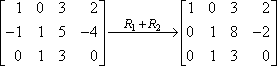
In diesem Fall bedeutet das „R1 + R2“ auf dem Pfeil „Ich habe Zeile eins zu Zeile zwei addiert, und das ist das Ergebnis“. Da sich Zeile eins nicht geändert hat und wir mit Zeile drei nichts gemacht haben, werden diese Zeilen unverändert in die neue Matrix kopiert.
Top | 1 | 2 | Zurück zum Index Weiter >>
|
Zitiere diesen Artikel als: |
Stapel, Elizabeth. „Matrix Row Operations.“ Purplemath. Available from 2016
|