Klassifikation durch Diskriminanzanalyse
Lassen Sie uns sehen, wie die LDA als überwachte Klassifikationsmethode abgeleitet werden kann. Betrachten wir ein allgemeines Klassifizierungsproblem: Eine Zufallsvariable X gehört zu einer von K Klassen, mit einigen klassenspezifischen Wahrscheinlichkeitsdichten f(x). Eine Diskriminanzregel versucht, den Datenraum in K disjunkte Regionen zu unterteilen, die alle Klassen repräsentieren (man stelle sich die Felder auf einem Schachbrett vor). Mit diesen Regionen bedeutet eine Klassifizierung durch Diskriminanzanalyse einfach, dass wir x der Klasse j zuordnen, wenn x in der Region j liegt. Die Frage ist nun, woher wir wissen, in welche Region die Daten x fallen. Natürlich können wir zwei Zuordnungsregeln befolgen:
- Maximum-Likelihood-Regel: Wenn wir annehmen, dass jede Klasse mit gleicher Wahrscheinlichkeit auftreten könnte, dann ordnen wir x der Klasse j zu, wenn

- Bayes’sche Regel: Wenn wir die Klassenpriorwahrscheinlichkeiten π kennen, dann ordnen wir x der Klasse j zu, wenn

Lineare und quadratische Diskriminanzanalyse
Wenn wir annehmen, dass die Daten aus einer multivariaten Gauß-Verteilung stammen, d.d. h. die Verteilung von X kann durch ihren Mittelwert (μ) und ihre Kovarianz (Σ) charakterisiert werden, lassen sich explizite Formen der oben genannten Zuordnungsregeln erhalten. Nach der Bayes’schen Regel ordnen wir die Daten x der Klasse j zu, wenn sie die höchste Wahrscheinlichkeit unter allen K Klassen für i = 1,…,K:

Die obige Funktion wird Diskriminanzfunktion genannt. Man beachte die Verwendung der log-likelihood hier. Mit anderen Worten: Die Diskriminanzfunktion gibt an, wie wahrscheinlich es ist, dass Daten x zu den einzelnen Klassen gehören. Die Entscheidungsgrenze, die zwei beliebige Klassen, k und l, trennt, ist also die Menge von x, bei der zwei Diskriminanzfunktionen denselben Wert haben. Daher sind alle Daten, die auf die Entscheidungsgrenze fallen, in beiden Klassen gleich wahrscheinlich (wir konnten uns nicht entscheiden).
LDA entsteht in dem Fall, in dem wir gleiche Kovarianz zwischen K Klassen annehmen. Das heißt, anstelle einer Kovarianzmatrix pro Klasse haben alle Klassen die gleiche Kovarianzmatrix. Dann erhalten wir die folgende Diskriminanzfunktion:

Bei dieser Funktion handelt es sich um eine lineare Funktion in x. Somit ist auch die Entscheidungsgrenze zwischen einem beliebigen Klassenpaar eine lineare Funktion in x, daher der Name: lineare Diskriminanzanalyse. Ohne die Annahme gleicher Kovarianz hebt sich der quadratische Term in der Wahrscheinlichkeit nicht auf, so dass die resultierende Diskriminanzfunktion eine quadratische Funktion in x ist:

In diesem Fall ist die Entscheidungsgrenze quadratisch in x. Dies wird als quadratische Diskriminanzanalyse (QDA) bezeichnet.
Was ist besser? LDA oder QDA?
In realen Problemen sind die Populationsparameter in der Regel unbekannt und werden aus den Trainingsdaten als Stichprobenmittelwerte und Stichproben-Kovarianzmatrizen geschätzt. Während QDA im Vergleich zu LDA flexiblere Entscheidungsgrenzen zulässt, steigt auch die Anzahl der zu schätzenden Parameter schneller als bei LDA. Für LDA werden (p+1) Parameter benötigt, um die Diskriminanzfunktion in (2) zu konstruieren. Bei einem Problem mit K Klassen würden wir nur (K-1) solcher Diskriminanzfunktionen benötigen, wenn wir willkürlich eine Klasse als Basisklasse auswählen (indem wir die Wahrscheinlichkeit der Basisklasse von allen anderen Klassen abziehen). Daher ist die Gesamtzahl der geschätzten Parameter für LDA (K-1)(p+1).
Andererseits müssen für jede QDA-Diskriminantenfunktion in (3) der Mittelwertvektor, die Kovarianzmatrix und der Klassenprior geschätzt werden:
– Mittelwert: p
– Kovarianz: p(p+1)/2
– Klassenprior: 1
Gleichermaßen müssen wir für QDA (K-1){p(p+3)/2+1} Parameter schätzen.
Daher steigt die Anzahl der geschätzten Parameter bei LDA linear mit p, während die von QDA quadratisch mit p ansteigt. Wir würden erwarten, dass QDA eine schlechtere Leistung als LDA hat, wenn die Problemdimension groß ist.
Best of two worlds? Kompromiss zwischen LDA & QDA
Wir können einen Kompromiss zwischen LDA und QDA finden, indem wir die Kovarianzmatrizen der einzelnen Klassen regularisieren. Regularisierung bedeutet, dass wir den geschätzten Parametern eine bestimmte Beschränkung auferlegen. In diesem Fall verlangen wir, dass die individuelle Kovarianzmatrix durch einen Strafparameter zu einer gemeinsamen gepoolten Kovarianzmatrix schrumpft, z.B. α:

Die gemeinsame Kovarianzmatrix kann auch durch einen Strafparameter z.B. zu einer Identitätsmatrix regularisiert werden, β:

In Situationen, in denen die Anzahl der Eingangsvariablen die Anzahl der Stichproben stark übersteigt, kann die Kovarianzmatrix schlecht geschätzt werden. Eine Schrumpfung kann hoffentlich die Schätzung und die Klassifizierungsgenauigkeit verbessern. Dies wird in der folgenden Abbildung veranschaulicht.

Berechnung für LDA
Aus (2) und (3) geht hervor, dass die Berechnungen der Diskriminanzfunktionen vereinfacht werden können, wenn wir zuerst die Kovarianzmatrizen diagonalisieren. Das heißt, die Daten werden so transformiert, dass sie eine identische Kovarianzmatrix haben (keine Korrelation, Varianz von 1). Im Falle von LDA gehen wir bei der Berechnung wie folgt vor:

Schritt 2 sphärisiert die Daten, um eine identische Kovarianzmatrix im transformierten Raum zu erzeugen. Schritt 4 ergibt sich aus (2).
Nehmen wir ein Beispiel mit zwei Klassen, um zu sehen, was LDA wirklich tut. Nehmen wir an, es gibt zwei Klassen, k und l. Wir ordnen x der Klasse k zu, wenn

Die obige Bedingung bedeutet, dass die Klasse k mit größerer Wahrscheinlichkeit Daten x produziert als die Klasse l. Nach den vier oben beschriebenen Schritten schreiben wir
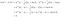
Das heißt, wir ordnen Daten x der Klasse k zu, wenn

Die abgeleitete Zuordnungsregel offenbart die Funktionsweise von LDA. Die linke Seite der Gleichung ist die Länge der orthogonalen Projektion von x* auf das Liniensegment, das die beiden Klassenmittelwerte verbindet. Die rechte Seite ist die Lage des Mittelpunkts des Segments, korrigiert um die Prioritätswahrscheinlichkeiten der Klassen. Im Wesentlichen klassifiziert LDA die kugelförmigen Daten nach dem nächstgelegenen Klassenmittelwert. Wir können hier zwei Beobachtungen machen:
- Der Entscheidungspunkt weicht vom Mittelpunkt ab, wenn die Klassenpriorwahrscheinlichkeiten nicht gleich sind, d.h. die Grenze wird in Richtung der Klasse mit einer geringeren Priorwahrscheinlichkeit verschoben.
- Die Daten werden auf den Raum projiziert, der durch die Klassenmittelwerte aufgespannt wird (die Multiplikation von x* und die Mittelwertsubtraktion auf der L.H.S. der Regel). Abstandsvergleiche werden dann in diesem Raum durchgeführt.