- Konnektivität ist ein grundlegendes Konzept der Graphentheorie. Es definiert, ob ein Graph zusammenhängend oder unzusammenhängend ist. Ohne Konnektivität ist es nicht möglich, einen Graphen von einem Scheitelpunkt zu einem anderen Scheitelpunkt zu durchqueren.
- Ein Graph wird als zusammenhängender Graph bezeichnet, wenn es einen Pfad zwischen jedem Paar von Scheitelpunkten gibt. Von jedem Scheitelpunkt zu jedem anderen Scheitelpunkt muss es einen Pfad geben, der durchlaufen werden kann. Dies wird als Konnektivität eines Graphen bezeichnet.
- Ein Graph wird als unverbunden bezeichnet, wenn es mehrere unverbundene Knoten und Kanten gibt.
- Die Theorien über die Konnektivität von Graphen sind wichtig für Netzwerkanwendungen, Routing von Transportnetzwerken, Netzwerktoleranz usw.
Beispiel
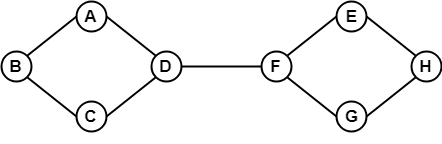
Im obigen Beispiel ist es möglich, von einem Knoten zu einem anderen zu reisen. In diesem Fall kann man von B nach H reisen, indem man den Pfad B -> A -> D -> F -> E -> H benutzt. Es handelt sich also um einen zusammenhängenden Graphen.
Beispiel
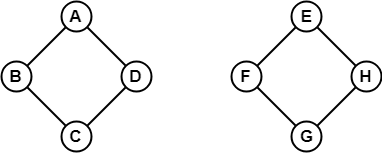
Im obigen Beispiel ist es nicht möglich, von B nach H zu reisen, weil es keinen direkten oder indirekten Pfad zwischen ihnen gibt. Daher handelt es sich um einen unverbundenen Graphen.
Lassen Sie uns einige grundlegende Konzepte der Konnektivität betrachten.
Cut Vertex
Ein einzelner Vertex, dessen Entfernung einen Graphen trennt, wird Cut-Vertex genannt.
Lassen Sie G einen verbundenen Graphen sein. Ein Knoten v von G heißt ein cut-vertex von G, wenn G-v (Entfernen von v aus G) einen unverbundenen Graphen ergibt.
Wenn wir einen Knoten aus einem Graphen entfernen, dann zerfällt der Graph in zwei oder mehr Graphen. Dieser Knoten wird Schnittknoten genannt.
Anmerkung: Sei G ein Graph mit n Knoten:
- Ein zusammenhängender Graph G kann maximal (n-2) Schnittknoten haben.
- Entfernt man einen Schnittknoten, kann ein Graph unverbunden bleiben.
- Das Entfernen eines Knotens kann die Anzahl der Komponenten in einem Graphen um mindestens eine erhöhen.
- Jeder nicht abhängige Knoten eines Baumes ist ein Schnittknoten.
Beispiel 1

Beispiel 2
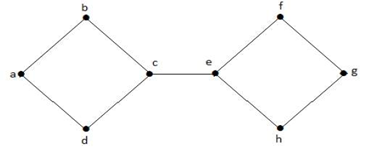
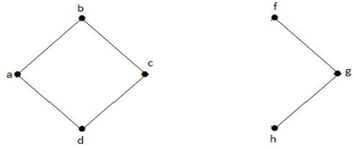
In dem obigen Graphen ist der Knoten ‚e‘ ein Schnittknoten. Nachdem der Knoten ‚e‘ aus dem obigen Graphen entfernt wurde, wird der Graph zu einem unverbundenen Graphen.
Cut Edge (Bridge)
Eine Cut-Edge oder Bridge ist eine einzelne Kante, deren Entfernung einen Graphen unverbunden macht.
Lassen Sie G ein verbundener Graph sein. Eine Kante e von G heißt eine Schnittkante von G, wenn G-e (Entfernen von e aus G) einen unverbundenen Graphen ergibt.
Wenn wir eine Kante aus einem Graphen entfernen, dann zerfällt der Graph in zwei oder mehr Graphen. Diese entfernte Kante wird Schnittkante oder Brücke genannt.
Anmerkung: Sei G ein Graph mit n Scheitelpunkten:
- Ein zusammenhängender Graph G kann höchstens (n-1) Schnittkanten haben.
- Entfernt man eine Schnittkante, kann ein Graph unverbunden bleiben.
- Das Entfernen einer Kante kann die Anzahl der Komponenten eines Graphen um höchstens eine erhöhen.
- Eine Schnittkante ‚e‘ darf nicht Teil eines Zyklus in G sein.
- Wenn eine Schnittkante existiert, dann muss auch ein Schnittknoten existieren, weil mindestens ein Knoten einer Schnittkante ein Schnittknoten ist.
- Wenn ein Schnittpunkt existiert, dann ist die Existenz einer Schnittkante nicht notwendig.
Beispiel 1
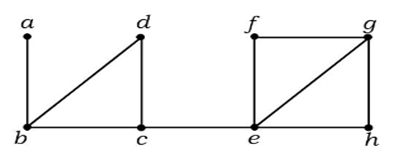
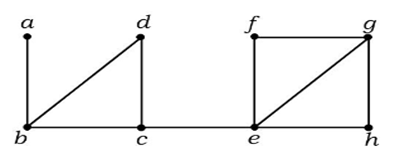
In dem obigen Graphen ist die Kante (c, e) eine Schnittkante. Nachdem man diese Kante aus dem obigen Graphen entfernt hat, wird der Graph ein unverbundener Graph.
Beispiel 2
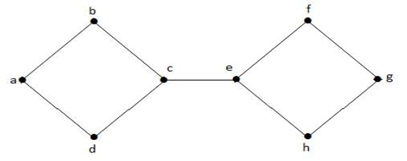
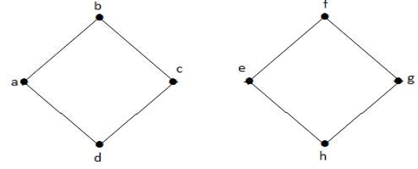
In dem obigen Graphen ist die Kante (c, e) eine Schnittkante. Nach dem Entfernen dieser Kante aus dem obigen Graphen wird der Graph zu einem unverbundenen Graphen.
Schnittmenge
In einem zusammenhängenden Graphen G ist eine Schnittmenge eine Menge S von Kanten mit den folgenden Eigenschaften:
- Das Entfernen aller Kanten in S trennt G.
- Die Entfernung einiger (aber nicht aller) Kanten in S führt nicht zur Trennung von G.
Beispiel 1
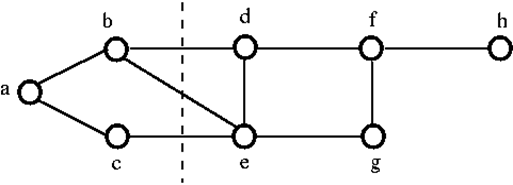
Um den obigen Graphen G zu trennen, müssen wir die drei Kanten entfernen, d.h. bd, be und ce. Wir können ihn nicht auflösen, indem wir nur zwei der drei Kanten entfernen. Daher ist {bd, be, ce} eine Schnittmenge.
Nach dem Entfernen der Schnittmenge aus dem obigen Graphen würde er wie folgt aussehen:
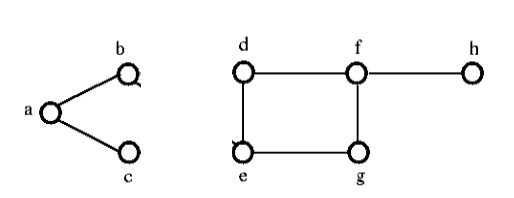
Kantenkonnektivität
Die Kantenkonnektivität eines zusammenhängenden Graphen G ist die minimale Anzahl von Kanten, deren Entfernung G unverbunden macht. Sie wird mit λ(G) bezeichnet.
Wenn λ(G) ≥ k ist, dann heißt der Graph G k-Kanten-verbunden.
Beispiel
Sehen wir uns ein Beispiel an,
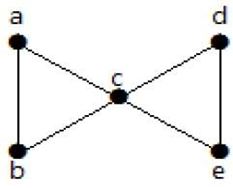
Aus dem obigen Graphen wird durch Entfernen von zwei minimalen Kanten der verbundene Graph zu einem unverbundenen Graph. Daher ist seine Kantenkonnektivität 2. Daher ist der obige Graph ein 2-Kanten-verbundener Graph.
Hier sind die folgenden vier Möglichkeiten, den Graphen durch Entfernen von zwei Kanten zu trennen:
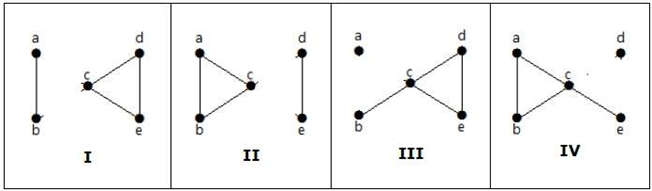
Vertex-Konnektivität
Die Konnektivität (oder Vertex-Konnektivität) eines verbundenen Graphen G ist die minimale Anzahl von Scheitelpunkten, deren Entfernung dazu führt, dass G nicht mehr verbunden ist oder auf einen trivialen Graph reduziert wird. Sie wird mit K(G) bezeichnet.
Der Graph heißt k-verbunden oder k-vertex-verbunden, wenn K(G) ≥ k. Um einen Vertex zu entfernen, müssen auch die zu ihm gehörenden Kanten entfernt werden.
Beispiel
Sehen wir uns ein Beispiel an:
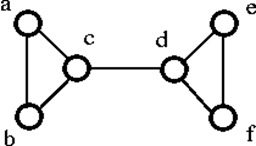
Der obige Graph G kann durch Entfernen eines einzigen Vertexes entweder ‚c‘ oder ‚d‘ getrennt werden. Daher ist seine Knotenkonnektivität 1. Daher ist er ein Graph mit 1 Verbindung.