GeeksforGeeks

Voraussetzung – Graphentheorie Grundlagen – Satz 1
Ein Graph ist eine Struktur, die aus einer Menge von Objekten besteht, bei der einige Paare von Objekten in gewissem Sinne „verwandt“ sind. Die Objekte des Graphen entsprechen den Eckpunkten und die Beziehungen zwischen ihnen den Kanten. Ein Graph wird diagrammatisch als eine Menge von Punkten dargestellt, die Scheitelpunkte darstellen, die durch Linien oder Kurven verbunden sind, die Kanten darstellen.
Formell,

„Ein Graph besteht aus , einer nicht leeren Menge von Scheitelpunkten (oder Knoten) und , einer Menge von Kanten. Jeder Kante sind entweder ein oder zwei Scheitelpunkte zugeordnet, die als Endpunkte bezeichnet werden.“

Typen von Graphen:Es gibt verschiedene Arten von Graphen, die sich durch die Anzahl der Kanten, ihre Richtung, ihr Gewicht usw. unterscheiden.

1. Einfacher Graph – Ein Graph, in dem jede Kante zwei verschiedene Scheitelpunkte verbindet und in dem keine zwei Kanten das gleiche Paar von Scheitelpunkten verbinden, wird als einfacher Graph bezeichnet. Betrachten wir zum Beispiel den folgenden Graphen –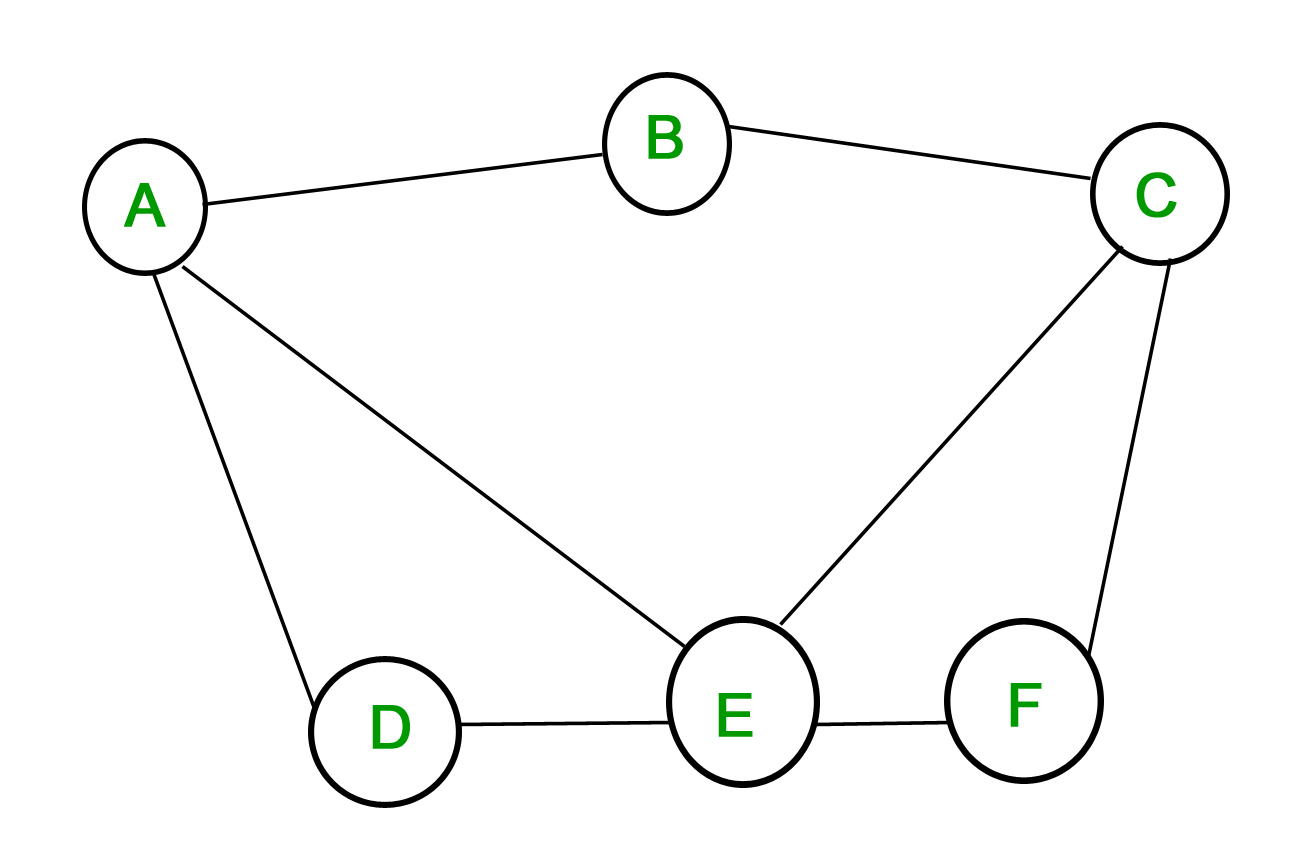

Der obige Graph ist ein einfacher Graph, da kein Scheitelpunkt eine Selbstschleife hat und keine zwei Scheitelpunkte mehr als eine Kante haben, die sie verbindet.
Die Kanten werden durch die Scheitelpunkte bezeichnet, die sie verbinden – ist die Kante, die die Scheitelpunkte und verbindet.

2. Multigraph – Ein Graph, in dem mehrere Kanten das gleiche Paar von Scheitelpunkten verbinden können, wird als Multigraph bezeichnet.
Da es mehrere Kanten zwischen dem gleichen Paar von Scheitelpunkten geben kann, gibt die Multiplizität der Kante die Anzahl der Kanten zwischen zwei Scheitelpunkten an.

Der obige Graph ist ein Multigraph, da es mehrere Kanten zwischen und gibt. Die Multiplizität der Kante ist 2.

In einigen Graphen, anders als in dem oben gezeigten, sind die Kanten gerichtet. Das bedeutet, dass die Beziehung zwischen den Objekten nur in eine Richtung und nicht in zwei Richtungen verläuft. Die Richtung der Kanten kann in einigen Anwendungen wichtig sein.

Abhängig davon, ob die Kanten gerichtet sind oder nicht, können wir gerichtete und ungerichtete Graphen haben. Diese Eigenschaft kann auf einfache Graphen und Multigraphen erweitert werden, um einfache gerichtete oder ungerichtete einfache Graphen und gerichtete oder ungerichtete Multigraphen zu erhalten.

Grundlegende Graphenterminologie:

In der obigen Diskussion wurden bereits einige Begriffe in Bezug auf Graphen erklärt, wie z.B. Knoten, Kanten, gerichtete und ungerichtete Kanten usw. Es gibt weitere Begriffe, die Eigenschaften von Knoten und Kanten beschreiben.

• Adjazenz – In einem Graphen werden zwei Knoten und als benachbart bezeichnet, wenn sie die Endpunkte einer Kante sind. Man sagt, dass die Kante mit den Scheitelpunkten zusammenfällt.
  Wenn die Kante gerichtet ist, sagt man, dass an angrenzt und dass an angrenzt. In diesem Fall ist der erste Scheitelpunkt und der letzte Scheitelpunkt.
• Grad – Der Grad eines Scheitelpunktes ist die Anzahl der mit ihm verbundenen Kanten, mit Ausnahme der Selbstschleife, die doppelt zum Grad des Scheitelpunktes beiträgt. Der Grad eines Scheitelpunkts wird als bezeichnet.
  Bei gerichteten Graphen wird der Grad weiter in In-Grad und Out-Grad unterteilt. Der In-Grad eines Scheitelpunkts ist die Anzahl der Kanten mit dem gegebenen Scheitelpunkt als Endscheitelpunkt. Der Ausgangsgrad eines Scheitelpunkts ist die Anzahl der Kanten, bei denen der gegebene Scheitelpunkt der Anfangsscheitelpunkt ist. Der Eingangsgrad wird als und der Ausgangsgrad als bezeichnet.
  In dem oben gezeigten gerichteten Graphen, der Flüge zwischen Städten darstellt, ist der Eingangsgrad des Scheitelpunkts „Delhi“ beispielsweise 3 und sein Ausgangsgrad ist ebenfalls 3.

Anmerkung: Wenn ein Scheitelpunkt den Grad Null hat, wird er isoliert genannt. Wenn der Grad eins ist, nennt man ihn pendant.

Handshaking Theorem :

Was erhält man, wenn man die Grade aller Eckpunkte eines Graphen addiert. Im Falle eines ungerichteten Graphen trägt jede Kante zweimal bei, einmal für ihren Anfangsknoten und einmal für ihren Endknoten. Die Summe der Grade ist also gleich der doppelten Anzahl der Kanten. Diese Tatsache ist im Handshaking-Theorem festgehalten.

Let  be an undirected graph with  edges. ThenIn case G is a directed graph,

Das Handshaking-Theorem für ungerichtete Graphen hat ein interessantes Ergebnis –

An undirected graph has an even number of vertices of odd degree.

Beweis : Seien und die Mengen von Scheitelpunkten mit geradem bzw. ungeradem Grad.
Wir wissen durch den Handshake-Satz, dass,

So,

Die Summe der Grade der Scheitelpunkte mit geraden Graden ist gerade. Die LHS ist ebenfalls gerade, was bedeutet, dass die Summe der Grade der Scheitelpunkte mit ungeraden Graden gerade sein muss.
Die Anzahl der Scheitelpunkte mit ungeraden Graden ist also gerade.

Einige spezielle einfache Graphen:

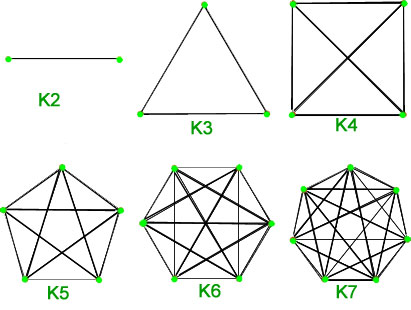
1. Vollständige Graphen – Ein einfacher Graph von Scheitelpunkten, der genau eine Kante zwischen jedem Paar von Scheitelpunkten hat, wird ein vollständiger Graph genannt. Ein vollständiger Graph mit Scheitelpunkten wird mit bezeichnet. Die Gesamtzahl der Kanten ist n*(n-1)/2 bei n Scheitelpunkten im vollständigen Graphen.

2. Zyklen – Zyklen sind einfache Graphen mit Scheitelpunkten und Kanten . Ein Zyklus mit Scheitelpunkten wird als bezeichnet. Die Gesamtzahl der Kanten ist n bei n Scheitelpunkten im Zyklusgraphen.

3. Räder – Ein Rad ist genau wie ein Zyklus, mit einem zusätzlichen Scheitelpunkt, der mit jedem anderen Scheitelpunkt verbunden ist. Räder aus Scheitelpunkten mit einem zusätzlichen Scheitelpunkt werden mit bezeichnet. Die Gesamtzahl der Kanten beträgt 2*(n-1) bei n Scheitelpunkten im Radgraph.

4. Hyperwürfel – Der Hyperwürfel oder n-Würfel ist ein Graph mit Scheitelpunkten, die jeweils durch eine n-Bit-Zeichenkette dargestellt werden. Die Scheitelpunkte, die sich um höchstens 1 Bit unterscheiden, sind durch Kanten verbunden. Ein Hyperwürfel mit Scheitelpunkten wird mit bezeichnet. Die Gesamtzahl der Kanten ist n* mit Scheitelpunkten im Würfelgraphen.

5. Bipartite Graphen – Ein einfacher Graph heißt bipartit, wenn seine Knotenmenge in zwei disjunkte Mengen unterteilt werden kann, so dass jede Kante in ihren Anfangsknoten in der ersten Menge und den Endknoten in der zweiten Menge hat. Die Gesamtzahl der Kanten ist (n*m) mit (n+m) Scheitelpunkten in einem bipartiten Graphen.

Theorem – Ein einfacher Graph ist dann und nur dann bipartit, wenn es möglich ist, jedem Scheitelpunkt des Graphen eine von zwei
unterschiedlichen Farben zuzuordnen, so dass keine zwei benachbarten Scheitelpunkte die
gleiche Farbe haben.

Ein zweiseitiger Graph mit und Scheitelpunkten in seinen beiden disjunkten Teilmengen heißt vollständig, wenn es eine Kante von jedem Scheitelpunkt der ersten Menge zu jedem Scheitelpunkt der zweiten Menge gibt, also insgesamt Kanten. Ein vollständiger zweiseitiger Graph mit Scheitelpunkten in der ersten Menge und Scheitelpunkten in der zweiten Menge wird als bezeichnet.

GATE CS Corner Questions

Das Üben der folgenden Fragen wird Ihnen helfen, Ihr Wissen zu testen. Alle Fragen wurden in GATE in den vergangenen Jahren oder in GATE Mock Tests gestellt. Es wird dringend empfohlen, dass Sie sie üben.

1. GATE CS 2013, Frage 25
2. GATE CS 2014 Set-1, Frage 61
3. GATE CS 2006, Frage 71
4. GATE CS 2002, Frage 25
5. GATE CS 2004, Frage 37
6. GATE CS 2014 Set-2, Frage 13

Referenzen-

Graphen – Wikipedia
Diskrete Mathematik und ihre Anwendungen, von Kenneth H Rosen

Dieser Artikel wurde von Chirag Manwani beigetragen. Wenn dir GeeksforGeeks gefällt und du einen Beitrag leisten möchtest, kannst du auch einen Artikel unter contribute.geeksforgeeks.org schreiben oder deinen Artikel an [email protected] schicken. Dein Artikel wird auf der GeeksforGeeks-Hauptseite erscheinen und anderen Geeks helfen.