Chemische Kinetik
Chemische Kinetik
Sie sind vielleicht mit Säure-Base-Titrationen vertraut, bei denen Phenolphthalein als Endpunktindikator verwendet wird. Vielleicht ist Ihnen jedoch nicht aufgefallen, was passiert, wenn man eine Lösung, die Phenolphthalein in Gegenwart einer überschüssigen Base enthält, einige Minuten stehen lässt. Obwohl die Lösung anfangs eine rosa Farbe hat, wird sie allmählich farblos, da das Phenolphthalein mit dem OH-Ion in einer stark basischen Lösung reagiert.
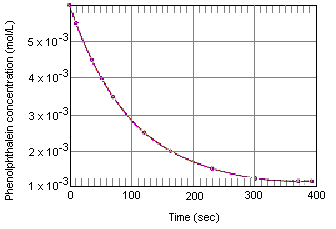
Die folgende Tabelle zeigt, was mit der Konzentration von Phenolphthalein in einer Lösung geschieht, die anfangs 0,005 M Phenolphthalein und 0,61 M OH-Ion enthielt. Wie Sie sehen können, wenn diese Daten in das nachstehende Diagramm eingetragen werden, nimmt die Phenolphthaleinkonzentration über einen Zeitraum von etwa vier Minuten um den Faktor 10 ab.
Experimentelle Daten für die Reaktion zwischen Phenolphthalein und überschüssiger Base
Experimente wie das, das uns die Daten in der obigen Tabelle geliefert hat, werden als Messungen der chemischen Kinetik (von einem griechischen Wortstamm, der „sich bewegen“ bedeutet) klassifiziert. Eines der Ziele dieser Experimente ist es, die Reaktionsgeschwindigkeit zu beschreiben, d. h. die Geschwindigkeit, mit der die Reaktanten in die Produkte der Reaktion umgewandelt werden.
Der Begriff „Geschwindigkeit“ wird häufig verwendet, um die Änderung einer Menge zu beschreiben, die pro Zeiteinheit auftritt. Die Inflationsrate ist zum Beispiel die Veränderung der durchschnittlichen Kosten einer Sammlung von Standardartikeln pro Jahr. Die Geschwindigkeit, mit der sich ein Objekt durch den Raum bewegt, ist die pro Zeiteinheit zurückgelegte Strecke, z. B. Meilen pro Stunde oder Kilometer pro Sekunde. In der chemischen Kinetik ist die zurückgelegte Strecke die Änderung der Konzentration einer der Komponenten der Reaktion. Die Geschwindigkeit einer Reaktion ist also die Änderung der Konzentration eines der Reaktanten![]() (X)
(X)![]() , die während einer bestimmten Zeitspanne
, die während einer bestimmten Zeitspanne![]() t auftritt.
t auftritt.
![]()
Praxisaufgabe 1:
Berechnen Sie anhand der Daten in der obigen Tabelle die Geschwindigkeit, mit der Phenolphthalein mit dem OH-Ion in jedem der folgenden Zeiträume reagiert:
(a) Im ersten Zeitintervall, wenn die Phenolphthaleinkonzentration von 0,0050 M auf 0,0045 M fällt.
(b) Während des zweiten Zeitintervalls, wenn die Konzentration von 0,0045 M auf 0,0040 M fällt.
(c) Während des dritten Zeitintervalls, wenn die Konzentration von 0,0040 M auf 0,0035 M fällt.
Klicken Sie hier, um Ihre Antwort auf Übungsaufgabe 1 zu überprüfen.
Klicken Sie hier, um die Lösung der Übungsaufgabe 1 zu sehen.
![]()
Sofortige Reaktionsgeschwindigkeiten und das Geschwindigkeitsgesetz für eine Reaktion
Die Geschwindigkeit der Reaktion zwischen Phenolphthalein und dem OH-Ion ist nicht konstant; sie ändert sich mit der Zeit. Wie bei den meisten Reaktionen nimmt die Geschwindigkeit dieser Reaktion allmählich ab, wenn die Reaktanten verbraucht werden. Das bedeutet, dass sich die Reaktionsgeschwindigkeit ändert, während sie gemessen wird.
Um den Fehler zu minimieren, der dadurch in unsere Messungen einfließt, scheint es ratsam, die Reaktionsgeschwindigkeit über Zeiträume zu messen, die im Vergleich zu der Zeit, die für das Auftreten der Reaktion benötigt wird, kurz sind. Wir könnten zum Beispiel versuchen, die unendlich kleine Änderung der Konzentration![]() d(X)
d(X)![]() zu messen, die in einer unendlich kurzen Zeitspanne von t auftritt. Das Verhältnis dieser Mengen wird als momentane Reaktionsgeschwindigkeit bezeichnet.
zu messen, die in einer unendlich kurzen Zeitspanne von t auftritt. Das Verhältnis dieser Mengen wird als momentane Reaktionsgeschwindigkeit bezeichnet.
![]()
Die momentane Reaktionsgeschwindigkeit zu einem beliebigen Zeitpunkt kann aus einem Diagramm der Konzentration des Reaktanten (oder des Produkts) im Verhältnis zur Zeit berechnet werden. Das folgende Diagramm zeigt, wie die Reaktionsgeschwindigkeit für die Zersetzung von Phenolphthalein aus einem Diagramm der Konzentration über der Zeit berechnet werden kann. Die Reaktionsgeschwindigkeit zu einem beliebigen Zeitpunkt ist gleich der Steigung einer Tangente an diese Kurve zu diesem Zeitpunkt.
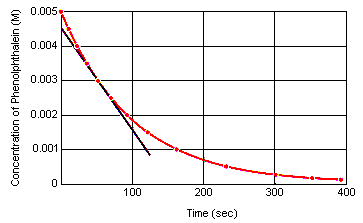
Die momentane Reaktionsgeschwindigkeit kann zu jedem Zeitpunkt zwischen dem Zeitpunkt, zu dem die Reagenzien gemischt werden, und dem Zeitpunkt, zu dem die Reaktion das Gleichgewicht erreicht, gemessen werden.Die Extrapolation dieser Daten zurück zu dem Zeitpunkt, zu dem die Reagenzien gemischt werden, ergibt die anfängliche momentane Reaktionsgeschwindigkeit.
![]()
Ratengesetze und Ratenkonstanten
Ein interessantes Ergebnis erhält man, wenn man die momentane Reaktionsgeschwindigkeit an verschiedenen Punkten entlang der Kurve im Diagramm im vorigen Abschnitt berechnet. Die Reaktionsgeschwindigkeit an jedem Punkt dieser Kurve ist direkt proportional zur Konzentration von Phenolphthalein zu diesem Zeitpunkt.
Rate = k(Phenolphthalein)
Da es sich bei dieser Gleichung um ein experimentelles Gesetz handelt, das die Geschwindigkeit der Reaktion beschreibt, wird sie als Geschwindigkeitsgesetz für die Reaktion bezeichnet. Die Proportionalitätskonstante, k, wird als Geschwindigkeitskonstante bezeichnet.
Praxisaufgabe 2:
Berechnen Sie die Geschwindigkeitskonstante für die Reaktion zwischen Phenolphthalein und dem OH–Ion, wenn die momentane Reaktionsgeschwindigkeit 2,5 x 10-5 Mol pro Liter pro Sekunde beträgt, wenn die Konzentration von Phenolphthalein 0,0025 M beträgt.
Klicken Sie hier, um Ihre Antwort zu Praxisaufgabe 2 zu überprüfen.
Klicken Sie hier, um die Lösung zu Praxisaufgabe 2 zu sehen.
Praxisaufgabe 3:
Berechnen Sie anhand der Geschwindigkeitskonstante für die Reaktion zwischen Phenolphthalein und dem OH-Ion die anfängliche momentane Reaktionsgeschwindigkeit für die in der vorstehenden Tabelle aufgeführten Versuchsdaten.
Klicken Sie hier, um Ihre Antwort auf die Übungsaufgabe 3 zu überprüfen.
Klicken Sie hier, um die Lösung der Übungsaufgabe 3 zu sehen.
![]()
Verschiedene Arten, die Reaktionsgeschwindigkeit auszudrücken
Es gibt normalerweise mehr als eine Möglichkeit, die Geschwindigkeit einer Reaktion zu messen. Wir können zum Beispiel die Zersetzung von Iodwasserstoff untersuchen, indem wir die Geschwindigkeit messen, mit der entweder H2 oder I2 in der folgenden Reaktion gebildet wird, oder die Geschwindigkeit, mit der HI verbraucht wird.
2 HI(g) H2(g) + I2(g)
Experimentell stellen wir fest, dass die Geschwindigkeit, mit der I2 gebildet wird, proportional zum Quadrat der HI-Konzentration zu jedem Zeitpunkt ist.
![]()
Was würde passieren, wenn wir die Geschwindigkeit, mit der H2 gebildet wird, untersuchen?
![]()
Was würde passieren, wenn wir die Geschwindigkeit, mit der HI in dieser Reaktion verbraucht wird, untersuchen? Da HI verbraucht wird, muss die Änderung seiner Konzentration eine negative Zahl sein. Gemäß der Konvention wird die Reaktionsgeschwindigkeit immer als positive Zahl angegeben. Daher müssen wir das Vorzeichen ändern, bevor wir die Reaktionsgeschwindigkeit für einen in der Reaktion verbrauchten Stoff angeben.
![]()
Das negative Vorzeichen erfüllt zwei Aufgaben. Mathematisch gesehen wandelt es eine negative Änderung der Konzentration von HI in eine positive Rate um. Physikalisch gesehen erinnert es uns daran, dass die Konzentration des Reaktanten mit der Zeit abnimmt.
Wie ist das Verhältnis zwischen der Reaktionsgeschwindigkeit, die man erhält, wenn man die Bildung von H2 oder I2 beobachtet, und der Geschwindigkeit, die man erhält, wenn man das Verschwinden von HI beobachtet? Die Stöchiometrie der Reaktion besagt, dass für jedes gebildete Molekül H2 oder I2 zwei HI-Moleküle verbraucht werden. Das bedeutet, dass die Zersetzungsgeschwindigkeit von HI doppelt so hoch ist wie die Geschwindigkeit, mit der H2 und I2 gebildet werden. Diese Beziehung lässt sich wie folgt in eine mathematische Gleichung umwandeln.
![]()
Die Geschwindigkeitskonstante, die man aus der Untersuchung der Geschwindigkeit der Bildung von H2 und I2 in dieser Reaktion (k) erhält, ist also nicht dieselbe wie die Geschwindigkeitskonstante, die man erhält, wenn man die Geschwindigkeit des Verbrauchs von HI beobachtet (k‘)
Praxisaufgabe 4:
Berechnen Sie die Geschwindigkeit, mit der HI in der folgenden Reaktion in dem Moment verschwindet, in dem I2 mit einer Geschwindigkeit von 1.8 x 10-6 Mol pro Liter pro Sekunde gebildet wird:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Klicken Sie hier, um Ihre Antwort zu Übungsaufgabe 4 zu überprüfen.
Klicken Sie hier, um eine Lösung zu Übungsaufgabe 4 zu sehen.
![]()
Das Ratengesetz im Vergleich zur Stöchiometrie einer Reaktion
In den 1930er Jahren untersuchten Sir Christopher Ingold und seine Mitarbeiter an der University of London die Kinetik von Substitutionsreaktionen wie der folgenden.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Sie fanden heraus, dass die Geschwindigkeit dieser Reaktion proportional zu den Konzentrationen der beiden Reaktanten ist.
Rate = k(CH3Br)(OH-)
Als sie eine ähnliche Reaktion mit einem etwas anderen Ausgangsmaterial durchführten, erhielten sie ähnliche Produkte.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Aber jetzt war die Reaktionsgeschwindigkeit proportional zur Konzentration von nur einem der Reaktanten.
Rate = k((CH3)3CBr)
Diese Ergebnisse verdeutlichen einen wichtigen Punkt: Das Geschwindigkeitsgesetz für eine Reaktion kann nicht aus der Stöchiometrie der Reaktion vorhergesagt werden; es muss experimentell bestimmt werden. Manchmal stimmt das Geschwindigkeitsgesetz mit dem überein, was wir aufgrund der Stöchiometrie der Reaktion erwarten.
2 HI(g) H2(g) + I2(g)
Rate = k(HI)2
Oft, ist es jedoch nicht.
| 2 N2O5(g) |
Rate = k(N2O5) |
![]()
Ordnung der Molekularität
Einige Reaktionen laufen in einem einzigen Schritt ab. Die Reaktion, bei der ein Chloratom von ClNO2 auf NO übertragen wird, um NO2 und ClNO zu bilden, ist ein gutes Beispiel für eine einstufige Reaktion.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Andere Reaktionen erfolgen in einer Reihe von Einzelschritten. N2O5 z.B. zerfällt in einem dreistufigen Mechanismus zu NO2 und O2.
| Schritt 1: | N2O5 |
|
| Schritt 2: | NO2 + NO3 |
|
| Schritt 3: | NO + NO3 |
Die Schritte einer Reaktion werden nach der Molekularität klassifiziert, die die Anzahl der verbrauchten Moleküle beschreibt. Wenn nur ein einziges Molekül verbraucht wird, wird der Schritt als unimolekular bezeichnet. Wenn zwei Moleküle verbraucht werden, handelt es sich um einen bimolekularen Schritt.
Praxisaufgabe 5:
Bestimmen Sie die Molekularität jedes Schritts in der Reaktion, durch die N2O5 zu NO2 und O2 zerfällt.
Klicken Sie hier, um Ihre Antwort auf Praxisaufgabe 5 zu überprüfen.
Klicken Sie hier, um eine Lösung für Praxisaufgabe 5 zu sehen.
Reaktionen können auch nach ihrer Reihenfolge klassifiziert werden. Die Zersetzung von N2O5 ist eine Reaktion erster Ordnung, weil die Reaktionsgeschwindigkeit von der Konzentration von N2O5 in der ersten Potenz abhängt.
Rate = k(N2O5)
Die Zersetzung von HI ist eine Reaktion zweiter Ordnung, weil die Reaktionsgeschwindigkeit von der Konzentration von HI in der zweiten Potenz abhängt.
Rate = k(HI)2
Wenn die Rate einer Reaktion von mehr als einem Reagenz abhängt, klassifizieren wir die Reaktion nach der Reihenfolge der einzelnen Reagenzien.
Praxisaufgabe 6:
Bestimmen Sie die Reihenfolge der Reaktion zwischen NO und O2 unter Bildung von NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Nehmen Sie das folgende Geschwindigkeitsgesetz für diese Reaktion an:
Rate = k(NO)2(O2)
Klicken Sie hier, um Ihre Antwort auf Praxisaufgabe 6 zu überprüfen.
Der Unterschied zwischen der Molekularität und der Ordnung einer Reaktion ist wichtig. Die Molekularität einer Reaktion oder eines Reaktionsschritts beschreibt, was auf molekularer Ebene geschieht. Die Reihenfolge einer Reaktion beschreibt, was auf der makroskopischen Ebene geschieht. Wir bestimmen die Reihenfolge einer Reaktion, indem wir beobachten, wie die Produkte einer Reaktion erscheinen oder die Reaktanten verschwinden. Die Molekularität der Reaktion ist etwas, das wir ableiten, um diese experimentellen Ergebnisse zu erklären.
![]()
Kollisionstheoretisches Modell chemischer Reaktionen
Das kollisionstheoretische Modell chemischer Reaktionen kann verwendet werden, um die beobachteten Geschwindigkeitsgesetze sowohl für einstufige als auch für mehrstufige Reaktionen zu erklären. Dieses Modell geht davon aus, dass die Geschwindigkeit eines jeden Reaktionsschritts von der Häufigkeit der Kollisionen zwischen den an diesem Schritt beteiligten Teilchen abhängt.
Die nachstehende Abbildung bietet eine Grundlage für das Verständnis der Auswirkungen des kollisionstheoretischen Modells für einfache, einstufige Reaktionen, wie die folgende.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
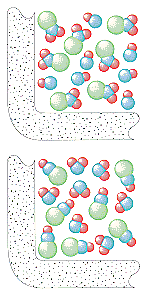
Die kinetische Molekulartheorie geht davon aus, dass die Anzahl der Zusammenstöße pro Sekunde in einem Gas von der Anzahl der Teilchen pro Liter abhängt. Die Rate, mit der NO2 und ClNO in dieser Reaktion gebildet werden, sollte daher direkt proportional zu den Konzentrationen von ClNO2 und NO sein.
Rate = k(ClNO2)(NO)
Das Modell der Kollisionstheorie legt nahe, dass die Rate eines jeden Reaktionsschritts proportional zu den Konzentrationen der in diesem Schritt verbrauchten Reagenzien ist. Das Geschwindigkeitsgesetz für eine einstufige Reaktion sollte daher mit der Stöchiometrie der Reaktion übereinstimmen.
Die folgende Reaktion verläuft beispielsweise in einer einzigen Stufe.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Wenn diese Moleküle in der richtigen Ausrichtung zusammenstoßen, kann ein Paar nichtbindender Elektronen am OH-Ion an das Kohlenstoffatom im Zentrum des CH3Br-Moleküls abgegeben werden, wie in der folgenden Abbildung gezeigt.
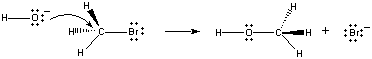
Wenn dies geschieht, bildet sich eine Kohlenstoff-Sauerstoff-Bindung zur gleichen Zeit, in der die Kohlenstoff-Brom-Bindung gebrochen wird. Das Endergebnis dieser Reaktion ist die Substitution eines OH-Ions durch ein Br-Ion. Da die Reaktion in einem einzigen Schritt abläuft, bei dem es zu Zusammenstößen zwischen den beiden Reaktanten kommt, ist die Geschwindigkeit dieser Reaktion proportional zur Konzentration der beiden Reaktanten.
Rate = k(CH3Br)(OH-)
Nicht alle Reaktionen laufen in einem einzigen Schritt ab. Die folgende Reaktion verläuft in drei Schritten, wie in der Abbildung unten gezeigt.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
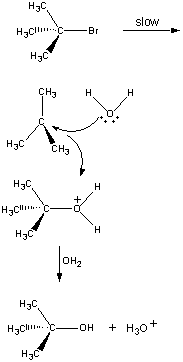
Im ersten Schritt dissoziiert das (CH3)3CBr-Molekül in ein Ionenpaar.
| Erster Schritt | 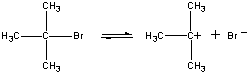 |
Das positiv geladene (CH3)3C+ Ion reagiert dann in einem zweiten Schritt mit Wasser.
| Zweiter Schritt | 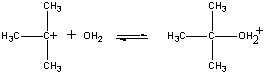 |
Das Produkt dieser Reaktion verliert dann im letzten Schritt ein Proton entweder an das OH-Ion oder an Wasser.
| Dritter Schritt | 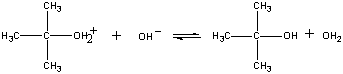 |
Der zweite und dritte Schritt in dieser Reaktion sind sehr viel schneller als der erste.
| (CH3)3CBr |
Slow step | |
| (CH3)3C+ + H2O |
Fast step | |
| (CH3)3COH2+ + OH- |
schneller Schritt |
Die Gesamtreaktionsgeschwindigkeit ist also mehr oder weniger gleich der Geschwindigkeit des ersten Schritts. Der erste Schritt wird daher als ratenbegrenzender Schritt in dieser Reaktion bezeichnet, weil er buchstäblich die Geschwindigkeit begrenzt, mit der die Produkte der Reaktion gebildet werden können. Da nur ein Reagenz am geschwindigkeitsbegrenzenden Schritt beteiligt ist, ist die Gesamtreaktionsgeschwindigkeit proportional zur Konzentration nur dieses Reagenzes.
Rate = k((CH3)3CBr)
Das Geschwindigkeitsgesetz für diese Reaktion weicht also von dem ab, was wir anhand der Stöchiometrie der Reaktion vorhersagen würden. Obwohl die Reaktion sowohl (CH3)3CBr als auch OH- verbraucht, ist die Geschwindigkeit der Reaktion nur proportional zur Konzentration von (CH3)3CBr.
Die Geschwindigkeitsgesetze für chemische Reaktionen können durch die folgenden allgemeinen Regeln erklärt werden.
Die Geschwindigkeit eines jeden Reaktionsschritts ist direkt proportional zu den Konzentrationen der Reagenzien, die in diesem Schritt verbraucht werden.
Das allgemeine Geschwindigkeitsgesetz für eine Reaktion wird durch die Abfolge der Schritte oder den Mechanismus bestimmt, durch die die Reaktanten in die Produkte der Reaktion umgewandelt werden.
Das allgemeine Geschwindigkeitsgesetz für eine Reaktion wird durch das Geschwindigkeitsgesetz für den langsamsten Schritt in der Reaktion dominiert.