Polynomielle Kleinstquadrat-Regression in Excel
Es gibt Fälle, in denen eine Best-Fit-Linie (d.h. ein Polynom erster Ordnung) nicht ausreicht. Kalibrierungsdaten, die offensichtlich gekrümmt sind, können oft mit einem Polynom zweiter (oder höherer) Ordnung zufriedenstellend angepasst werden. Kalibrierkurven in der Atomabsorption sind oft leicht gekrümmt; hier ein Beispiel aus einem anderen Tutorial.
Beispiel
Sie möchten die Bleikonzentration in Leitungswasser mit Graphitrohr-AAS analysieren. Die folgenden Daten wurden gesammelt. Geben Sie die Bleikonzentration im Leitungswasser in Form eines Konfidenzintervalls an.
| Bleikonz, ppb | Signal, A-s |
|---|---|
| Leerzeichen | 0.006 |
| 10.0 | 0.077 |
| 20.0 | 0.138 |
| 30.0 | 0.199 |
| 40.0 | 0.253 |
| 50.0 | 0.309 |
| 60.0 | 0.356 |
| Zapfwasserprobe | 0.278 |
Zunächst müssen die Daten in ein Excel-Arbeitsblatt eingegeben werden (zum Herunterladen der Datei auf das Bild klicken).
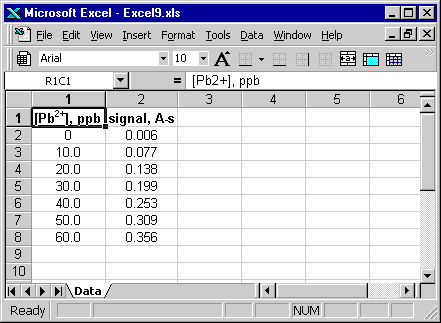
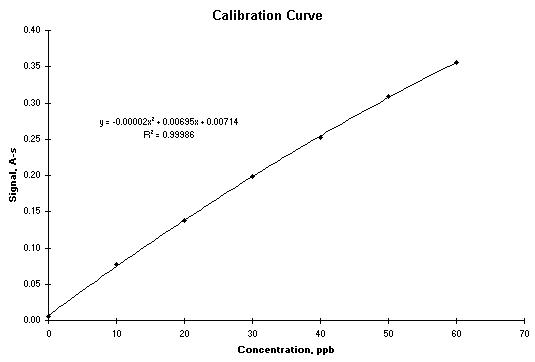
Eine Möglichkeit, eine polynomiale Regression durchzuführen, besteht darin, die entsprechende Trendlinie an die Daten anzupassen (und es gibt eine Reihe von Optionen zusätzlich zu Polynomen). Das Ergebnis ist im folgenden Screenshot zu sehen.
 |
Sehen Sie, wie dies gemacht wird. |
Während der obige Ansatz nützlich ist, um zusätzliche Informationen auf einem Kalibrierungsdiagramm bereitzustellen, fehlen einige Informationen (wie der Standardfehler in den Schätzungen oder die Standardabweichung in den Residuen). Es ist möglich, das Analysis ToolPak Add-In anzuwenden, um diese Informationen zu erhalten. Zunächst müssen Sie eine weitere Spalte erstellen, deren Zellen die quadrierten Konzentrationswerte enthalten.
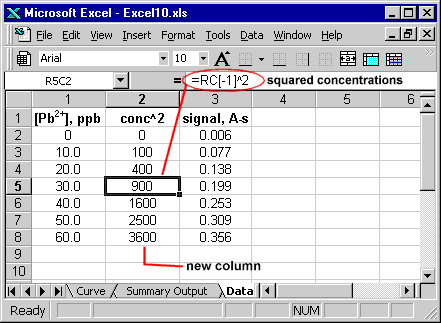
Jetzt können Sie das Analysis TookPak Add-in aufrufen. Markieren Sie bei der Auswahl des X-Bereichs den Block, der sowohl die Konzentrationen als auch deren quadrierte Werte enthält.
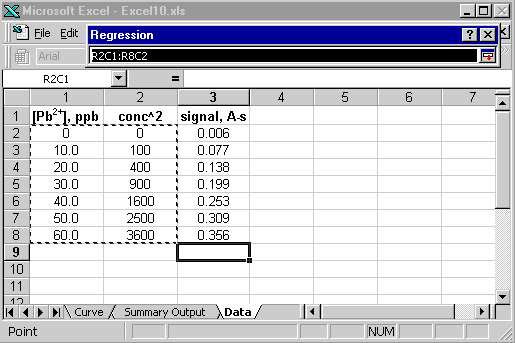
Das Dialogfeld für die Regression sollte dann wie folgt aussehen:
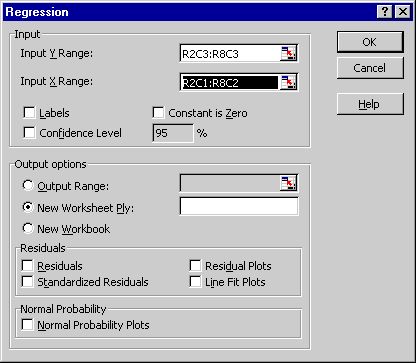
Die Ausgabe des Regressionsmoduls ist unten dargestellt. Klicken Sie auf das Bild, um die Excel-Datei herunterzuladen.
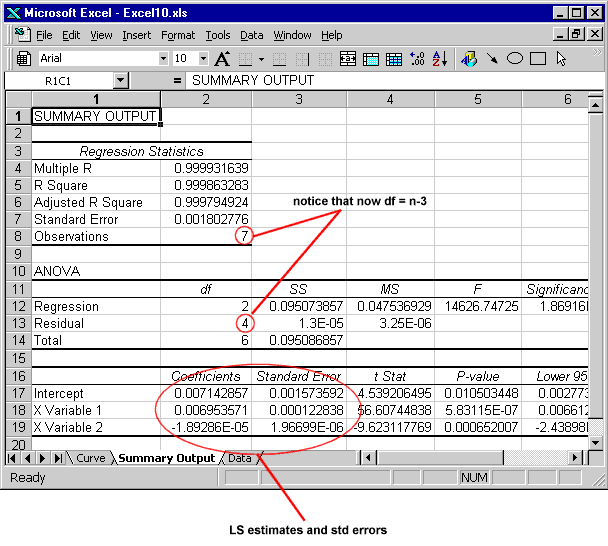
 |
Siehe eine Demonstration, wie Analysis ToolPak verwendet wird, um eine polynomiale Regression zweiter Ordnung durchzuführen |