Læringsresultater

  • Bestemme, om data eller et scenarie beskriver lineær eller geometrisk vækst
  • Identificere vækstrater, begyndelsesværdier eller punktværdier udtrykt mundtligt og grafisk, eller numerisk, og omsætte dem til et format, der kan bruges i beregninger
  • Beregne rekursive og eksplicitte ligninger for lineær og geometrisk vækst givet tilstrækkelige oplysninger og bruge disse ligninger til at foretage forudsigelser

At have en konstant ændringshastighed er det definerende kendetegn for lineær vækst. Hvis man plotter koordinatpar, der er forbundet med en konstant ændring, vil det resultere i en ret linje, hvilket er formen for lineær vækst. I dette afsnit vil vi formalisere en måde at beskrive lineær vækst på ved hjælp af matematiske termer og begreber. Ved afslutningen af dette afsnit vil du være i stand til at skrive både en rekursiv og eksplicitte ligninger for lineær vækst givet startbetingelser eller en ændringskonstant. Du vil også kunne genkende forskellen mellem lineær og geometrisk vækst givet en graf eller en ligning.

Linær (algebraisk) vækst

Forudsigelse af vækst

Marco er en samler af antikke sodavandsflasker. Hans samling indeholder i øjeblikket 437 flasker. Hvert år budgetterer han penge nok til at købe 32 nye flasker. Kan vi bestemme, hvor mange flasker han vil have om 5 år, og hvor lang tid det vil tage, før hans samling når op på 1000 flasker?

Selv om du sandsynligvis kunne løse begge disse spørgsmål uden en ligning eller formel matematik, vil vi formalisere vores tilgang til dette problem for at give et middel til at besvare mere komplicerede spørgsmål.

Sæt, at Pn repræsenterer det antal, eller den population, af flasker, som Marco har efter n år. Så P0 ville repræsentere antallet af flasker nu, P1 ville repræsentere antallet af flasker efter 1 år, P2 ville repræsentere antallet af flasker efter 2 år osv. Vi kunne beskrive, hvordan Marcos flaskesamling ændrer sig ved hjælp af:

P0 = 437

Pn = Pn-1 + 32

Dette kaldes et rekursivt forhold. En rekursiv relation er en formel, der relaterer den næste værdi i en rækkefølge til de foregående værdier. Her kan antallet af flasker i år n findes ved at lægge 32 til antallet af flasker i det foregående år, Pn-1. Ved hjælp af denne relation kan vi beregne:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 565 + 32 = 597

Vi har svaret på spørgsmålet om, hvor mange flasker Marco vil have om 5 år.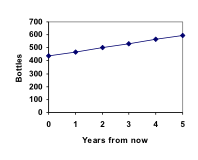

Det ville imidlertid kræve mange flere beregninger at løse, hvor lang tid det vil tage, før hans samling når op på 1000 flasker.

Mens rekursive relationer er glimrende til at beskrive enkelt og rent, hvordan en størrelse ændrer sig, er de ikke praktiske til at lave forudsigelser eller løse problemer, der strækker sig langt ud i fremtiden. Til det formål foretrækkes en lukket eller eksplicit form for relationen. En eksplicit ligning giver os mulighed for at beregne Pn direkte, uden at vi behøver at kende Pn-1. Selv om du måske allerede er i stand til at gætte den eksplicitte ligning, skal vi udlede den af den rekursive formel. Det kan vi gøre ved selektivt ikke at forenkle undervejs:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Du kan sikkert se mønsteret nu, og generalisere det

Pn = 437 + n(32) = 437 + 32n

Med denne ligning kan vi beregne, hvor mange flasker han vil have efter 5 år:

P5 = 437 + 32(5) = 437 + 160 = 597

Vi kan nu også løse, hvornår samlingen vil nå 1000 flasker ved at erstatte 1000 med Pn og løse n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Så Marco vil nå 1000 flasker om 18 år.

Trinene for bestemmelse af formlen og løsning af problemet med Marcos flaskesamling forklares i detaljer i de følgende videoer.

I dette eksempel voksede Marcos samling med det samme antal flasker hvert år. Denne konstante ændring er det definerende kendetegn for lineær vækst. Ved at plotte de værdier, som vi har beregnet for Marcos samling, kan vi se, at værdierne danner en lige linje, hvilket er formen for lineær vækst.

Linær vækst

Hvis en mængde starter ved størrelse P0 og vokser med d for hver tidsperiode, kan mængden efter n tidsperioder bestemmes ved hjælp af en af disse relationer:

Rekursiv form

Pn = Pn-1 + d

Eksplicit form

Pn = P0 + d n

I denne ligning repræsenterer d den fælles forskel – det beløb, som populationen ændrer sig, hver gang n stiger med 1.

Sammenhæng med tidligere læring: Hældning og skæringspunkt

Du genkender måske den fælles forskel, d, i vores lineære ligning som hældning. Faktisk burde hele den eksplicitte ligning se bekendt ud – det er den samme lineære ligning, som du lærte i algebra, sandsynligvis angivet som y = mx + b.

I den algebraiske standardligning y = mx + b var b y-interceptet, eller y-værdien, når x var nul. I den ligningsform, vi bruger, bruger vi P0 til at repræsentere denne begyndelsesværdi.

I ligningen y = mx + b skal du huske, at m var hældningen. Du husker det måske som “stigning over løb” eller ændringen i y divideret med ændringen i x. Uanset hvad repræsenterer det det samme som den fælles forskel, d, vi bruger – den mængde, som output Pn ændrer sig, når input n stiger med 1.

Ligningerne y = mx + b og Pn = P0 + d n betyder det samme og kan bruges på samme måde. Vi skriver det bare lidt anderledes.

Eksempler

Bestand af elge i en nationalskov blev målt til 12.000 i 2003, og blev igen målt til 15.000 i 2007. Hvis bestanden fortsætter med at vokse lineært med denne hastighed, hvad vil elgbestanden så være i 2014?

Vis løsning

Til at begynde med skal vi definere, hvordan vi vil måle n. Husk, at P0 er bestanden, når n = 0, så vi ønsker nok ikke bogstaveligt talt at bruge år 0. Da vi allerede kender befolkningen i 2003, lader os definere n = 0 til at være året 2003.

Så er P0 = 12.000.

Næst skal vi finde d. Husk, at d er væksten pr. tidsperiode, i dette tilfælde vækst pr. år. Mellem de to målinger er befolkningen vokset med 15.000-12.000 = 3.000, men det tog 2007-2003 = 4 år at vokse så meget. For at finde væksten pr. år kan vi dividere: 3.000 elge / 4 år = 750 elge på 1 år.

Alternativt kan du bruge hældningsformlen fra algebra til at bestemme den fælles forskel, idet du bemærker, at populationen er resultatet af formlen, og tiden er input.

d=hældning=\frac{\text{changeinoutput}}}{\text{changeinput}}}=\frac{15.000-12.000}{2007-2003}=\frac{3000}{4}=750

Vi kan nu skrive vores ligning i den form, som man foretrækker.

Rekursiv form

P0 = 12.000

Pn = Pn-1 + 750

Eksplicit form

Pn = 12.000 + 750(n)

For at besvare spørgsmålet skal vi først bemærke, at året 2014 vil være n = 11, da 2014 er 11 år efter 2003. Den eksplicitte form vil være nemmere at bruge til denne beregning:

P11 = 12.000 + 750(11) = 20.250 elg

Se mere om dette eksempel her.

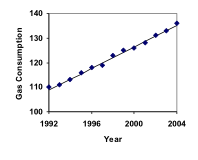
Benzinforbruget i USA har været støt stigende. Forbrugsdata fra 1992 til 2004 er vist nedenfor. Find en model for disse data, og brug den til at forudsige forbruget i 2016. Hvis tendensen fortsætter, hvornår vil forbruget så nå op på 200 mia. gallon?

År ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Forbrug (i mia. gallon) 110 111 113 116 118 119 119 123 125 126 128 131 133 136
Vis løsning

Plotting af disse data, ser det ud til at have et omtrent lineært forhold:

Selv om der findes mere avancerede statistiske teknikker, der kan bruges til at finde en ligning til at modellere dataene, kan vi for at få en idé om, hvad der sker, finde en ligning ved at bruge to dele af dataene – måske dataene fra 1993 og 2003.

Hvis man lader n = 0 svare til 1993, vil det give P0 = 111 milliarder gallon.

For at finde d skal vi vide, hvor meget gasforbruget steg hvert år i gennemsnit. Fra 1993 til 2003 steg gasforbruget fra 111 mia. gallon til 133 mia. gallon, hvilket svarer til en samlet ændring på 133 – 111 = 22 mia. gallon over 10 år. Dette giver os en gennemsnitlig ændring på 22 milliarder gallon / 10 år = 2,2 milliarder gallon om året.

Ækvivalent,

d=hældning=\frac{\text{changeinoutput}}}{\text{changeinput}}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 milliarder galloner om året

Vi kan nu skrive vores ligning i den form, som vi foretrækker.

Rekursiv form

P0 = 111

Pn = Pn-1 + 2.2

Eksplicit form

Pn = 111 + 2.2n

Beregning af værdier ved hjælp af den eksplicitte form og plotte dem med de oprindelige data viser, hvor godt vores model passer til dataene.

Vi kan nu bruge vores model til at lave forudsigelser om fremtiden, hvis vi antager, at den tidligere tendens fortsætter uændret. For at forudsige benzinforbruget i 2016:

n = 23 (2016 – 1993 = 23 år senere)

P23 = 111 + 2,2(23) = 161,6

Vores model forudsiger, at USA vil forbruge 161.6 milliarder gallon benzin i 2016, hvis den nuværende tendens fortsætter.

For at finde ud af, hvornår forbruget vil nå 200 milliarder gallon, skal vi sætte Pn = 200 og løse for n:

Pn = 200 Erstat Pn med vores model

111 + 2.2n = 200 Træk 111 fra begge sider

2.2n = 89 Divider begge sider med 2.2

n = 40.4545

Dette fortæller os, at forbruget vil nå 200 milliarder ca. 40 år efter 1993, hvilket vil være i år 2033.

Trinene for at nå frem til dette svar er beskrevet i den følgende video.

Udgifterne i dollars for et medlemskab af et fitnesscenter i n måneder kan beskrives ved den eksplicitte ligning Pn = 70 + 30n. Hvad fortæller denne ligning os?

Vis løsning

Værdien for P0 i denne ligning er 70, så den oprindelige startpris er 70 dollars. Dette fortæller os, at der skal være et startgebyr på 70 $ for at blive medlem af fitnesscentret.

Værdien for d i ligningen er 30, så omkostningerne stiger med 30 $ hver måned. Dette fortæller os, at det månedlige medlemsgebyr for fitnesscenteret er 30 $ om måneden.

Forklaringen på dette eksempel er nærmere beskrevet nedenfor.

Try It

Andelen af hjemmegående fædre i Canada er steget støt. Selv om tendensen ikke er perfekt lineær, er den ret lineær. Brug dataene fra 1976 og 2010 til at finde en eksplicit formel for antallet af hjemmegående fædre, og brug den derefter til at forudsige antallet i 2020.

År 1976 1984 1991 2000 2010
# af Bliv -at-home fathers 20610 28725 43530 47665 53555
Vis løsning

Lad n= 0 svare til 1976, så er P_0= 20.610.
Fra 1976 til 2010 steg antallet af hjemmegående fædre med 53.555 – 20.610 = 32.945
Dette skete over 34 år, hvilket giver en fælles forskellig d på 32.945 / 34 = 969.
P_n= 20.610 + 969n
Forudsiger vi for 2020, bruger vi n = 44, P(44) = 20.610 + 969(44) = 63.246 hjemmegående fædre i 2020.

Når gode modeller går galt

Når man bruger matematiske modeller til at forudsige fremtidig adfærd, er det vigtigt at huske på, at meget få tendenser vil fortsætte i det uendelige.

Eksempel

Sæt, at en fireårig dreng i øjeblikket er 39 tommer høj, og du får at vide, at du skal forvente, at han vokser 2,5 tommer om året.

Vi kan opstille en vækstmodel, hvor n = 0 svarer til 4 år.

Rekursiv form

P0 = 39

Pn = Pn-1 + 2,5

Eksplicit form

Pn = 39 + 2.5(n)

Så når han er 6 år gammel, vil vi forvente, at han er

P2 = 39 + 2,5(2) = 44 tommer høj

Alle matematiske modeller vil bryde sammen på et tidspunkt. Vi skal i hvert fald ikke forvente, at denne dreng fortsætter med at vokse med samme hastighed hele livet. Hvis han gjorde det, ville han i en alder af 50 år være

P46 = 39 + 2,5(46) = 154 tommer høj = 12,8 fod høj!

Når vi bruger en matematisk model, skal vi overveje, hvilke input der er rimelige at bruge. Når vi ekstrapolerer eller laver forudsigelser ind i fremtiden, antager vi, at modellen fortsat vil være gyldig.

Se en video-forklaring af denne opdeling af den lineære vækstmodel her.

Eksponentiel (geometrisk ) vækst

Populationsvækst

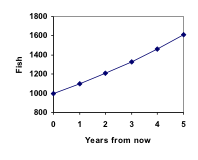
Sæt, at hvert år har kun 10 % af fiskene i en sø overlevende afkom. Hvis der sidste år var 100 fisk i søen, vil der nu være 110 fisk. Hvis der sidste år var 1000 fisk i søen, ville der nu være 1100 fisk. Hvis der ikke er nogen hæmmende faktorer, har befolkninger af mennesker og dyr tendens til at vokse med en procentdel af den eksisterende population hvert år.


Sæt, at vores sø begyndte med 1000 fisk, og at 10 % af fiskene har overlevende afkom hvert år. Da vi starter med 1000 fisk, er P0 = 1000. Hvordan beregner vi P1? Den nye population vil være den gamle population plus yderligere 10 %. Symbolsk:

P1 = P0 + 0,10P0

Bemærk, at dette kan kondenseres til en kortere form ved at faktorisere:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Mens 10 % er vækstraten, er 1,10 vækstmultiplikatoren. Bemærk, at 1,10 kan opfattes som “de oprindelige 100 % plus yderligere 10 %.”

For vores fiskebestand,

P1 = 1,10(1000) = 1100

Vi kan derefter beregne bestanden i de senere år:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Opmærksomheden henledes på, at i det første år voksede bestanden med 100 fisk, i det andet år voksede bestanden med 110 fisk, og i det tredje år voksede bestanden med 121 fisk.

Mens der er tale om en konstant procentvis vækst, stiger den faktiske stigning i antallet af fisk hvert år.

Graferer vi disse værdier, kan vi se, at denne vækst ikke virker helt lineær.

En gennemgang af dette fiskescenarie kan ses her:

For at få et bedre billede af, hvordan denne procentvise vækst påvirker tingene, har vi brug for en eksplicit form, så vi hurtigt kan beregne værdier længere ude i fremtiden.

Som vi gjorde for den lineære model, vil vi starte med at bygge ud fra den rekursive ligning:

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.10(1.103(1000)) = 1.104(1000)

Observation af et mønster, kan vi generalisere den eksplicitte form til at være:

Pn = 1.10n(1000), eller tilsvarende: Pn = 1000(1.10n)

Derfra kan vi hurtigt beregne antallet af fisk om 10, 20 eller 30 år:

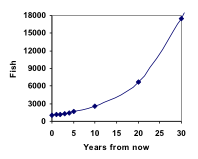
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Tilføjer vi disse værdier til vores graf, får vi en form, der bestemt ikke er lineær. Hvis vores fiskebestand var vokset lineært, med 100 fisk hvert år, ville bestanden kun have nået 4000 på 30 år, sammenlignet med næsten 18.000 med denne procentbaserede vækst, kaldet eksponentiel vækst.

En video, der demonstrerer den eksplicitte model for denne fiskehistorie, kan ses her:

I eksponentiel vækst vokser bestanden proportionalt med størrelsen af bestanden, så efterhånden som bestanden bliver større, vil den samme procentvise vækst give en større numerisk vækst.

Eksponentiel vækst

Hvis en mængde starter ved størrelse P0 og vokser med R% (skrevet som decimal, r) for hver tidsperiode, så kan mængden efter n tidsperioder bestemmes ved hjælp af en af disse to relationer:

Rekursiv form

Pn = (1+r) Pn-1

Eksplicit form

Pn = (1+r)n P0 eller tilsvarende: Pn = P0 (1+r)n

Vi kalder r for vækstrate.

Udtrykket (1+r) kaldes vækstmultiplikatoren eller det almindelige forhold.

Eksempel

Mellem 2007 og 2008 voksede Olympia, WA, med næsten 3 % til et indbyggertal på 245 tusinde mennesker. Hvis denne vækstrate skulle fortsætte, hvad ville Olympias befolkningstal så være i 2014?

Vis løsning

Som vi gjorde før, skal vi først definere, hvilket år der skal svare til n = 0. Da vi kender befolkningstallet i 2008, ville det give mening, at 2008 skulle svare til n = 0, så P0 = 245.000. Året 2014 ville så være n = 6.

Vi ved, at væksten er 3 %, hvilket giver r = 0,03.

Ved anvendelse af den eksplicitte form:

P6 = (1+0,03)6 (245.000) = 1,19405(245.000) = 292.542,25

Modellen forudsiger, at Olympia i 2014 vil have et indbyggertal på ca. 293 tusind mennesker.

Den følgende video forklarer dette eksempel i detaljer.

Evaluering af eksponenter på lommeregneren

For at evaluere udtryk som (1,03)6 vil det være lettere at bruge en lommeregner end at gange 1,03 med sig selv seks gange. De fleste videnskabelige lommeregnere har en knap til eksponenter. Den er typisk enten mærket som:

^ , yx , eller xy .

For at evaluere 1,036 ville vi skrive 1,03 ^ 6, eller 1,03 yx 6. Prøv det – du skulle få et svar omkring 1,1940523.

Prøv det

Indien er det næstmest befolkede land i verden med en befolkning i 2008 på ca. 1,14 milliarder mennesker. Befolkningen vokser med ca. 1,34 % hvert år. Hvis denne tendens fortsætter, hvad vil Indiens befolkning så vokse til i 2020?

Vis løsning

Ved anvendelse af n = 0 svarende til 2008 er P_12= (1+0,0134)12(1,14) = ca. 1.337 milliarder mennesker i 2020

Eksempler

En ven bruger ligningen Pn = 4600(1,072)n til at forudsige den årlige undervisningsafgift på et lokalt college. Hun siger, at formlen er baseret på år efter 2010. Hvad fortæller denne ligning os?

Vis løsning

I ligningen er P0 = 4600, hvilket er startværdien af undervisningsgebyret, når n = 0. Dette fortæller os, at undervisningsgebyret i 2010 var 4.600 dollars.

Vækstmultiplikatoren er 1,072, så væksten er 0,072 eller 7,2 %. Det fortæller os, at undervisningsgebyret forventes at vokse med 7,2 % hvert år.

Samlet set kan vi sige, at undervisningsgebyret i 2010 var 4.600 USD og forventes at vokse med 7,2 % hvert år.

Se følgende for at se dette eksempel udregnet.

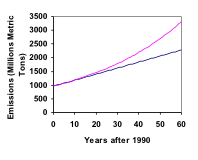
I 1990 var energiforbruget i boliger i USA ansvarlig for 962 millioner tons kuldioxidemissioner. I år 2000 var dette tal steget til 1182 mio. tons. Hvis emissionerne vokser eksponentielt og fortsætter med samme hastighed, hvad vil emissionerne så vokse til i 2050?

Vis løsning

Som tidligere svarer vi n = 0 til 1990, da det er året for det første stykke data, vi har. Det vil give P0 = 962 (millioner tons CO2). I denne opgave får vi ikke vækstraten, men får i stedet at vide, at P10 = 1182.

Når n = 10, ser den eksplicitte ligning således ud:

P10 = (1+r)10 P0

Vi kender værdien for P0, så den kan vi sætte ind i ligningen:

P10 = (1+r)10 962

Vi ved også, at P10 = 1182, så ved at indsætte det får vi

1182 = (1+r)10 962

Vi kan nu løse denne ligning for vækstrate, r. Vi starter med at dividere med 962.

\frac{1182}{962}={{(1+r)}^{10}}} Tag den 10. rod af begge sider

\sqrt{\frac{1182}{962}}}=1+r Træk 1 fra begge sider

r=\sqrt{\frac{1182}{962}}}-1=0,0208 = 2,08%

Så hvis emissionerne vokser eksponentielt, vokser de altså med ca. 2,08% om året. Vi kan nu forudsige emissionerne i 2050 ved at finde P60

P60 = (1+0,0208)60 962 = 3308,4 millioner tons CO2 i 2050

Se mere om dette eksempel her.

Afrunding

Som en bemærkning om afrunding skal du bemærke, at hvis vi havde afrundet vækstraten til 2,1 %, ville vores beregning af emissionerne i 2050 have været 3347. Hvis vi havde afrundet til 2 %, ville vores resultat have ændret sig til 3156. En meget lille forskel i vækstraterne bliver forstørret kraftigt ved eksponentiel vækst. Derfor anbefales det at afrunde vækstraten så lidt som muligt.

Hvis du skal afrunde, skal du beholde mindst tre betydende cifre – tal efter eventuelle foranstillede nuller. Så 0,4162 kan med rimelighed afrundes til 0,416. En vækstrate på 0,001027 kan med rimelighed afrundes til 0,00103.

Evaluering af rødder på lommeregneren

I det foregående eksempel skulle vi beregne den 10. rod af et tal. Dette er anderledes end at tage den grundlæggende kvadratrod, √. Mange videnskabelige lommeregnere har en knap til generelle rødder. Den er typisk mærket som:

\sqrt{x}

For at evaluere den 3. rod af 8 ville vi f.eks. enten skrive 3 \sqrt{{}} 8, eller 8 \sqrt{{{}} 8 \sqrt{{{}} 3, afhængigt af lommeregneren. Prøv det på din for at se, hvilken du skal bruge – du skulle få et svar på 2.

Hvis din lommeregner ikke har en generel rodknap, er alt ikke tabt. Du kan i stedet bruge eksponenternes egenskab, som siger, at:

\sqrt{a}={a}^{{\frac{1}{2}}}.

Så for at beregne den 3. rod af 8 kan du bruge din lommeregners eksponenttast til at evaluere 81/3. For at gøre dette skal du skrive:

8 yx ( 1 ÷ 3 )

Klammerne fortæller lommeregneren, at den skal dividere 1/3, før den laver eksponenten.

Afprøv det

Tallet af brugere på et socialt netværkssite var 45 tusind i februar, da de officielt gik på markedet, og voksede til 60 tusind i oktober. Hvis sitet vokser eksponentielt, og væksten fortsætter med samme hastighed, hvor mange brugere skal de så forvente to år efter, at de gik på børsen?

Vis løsning

Her vil vi måle n i måneder i stedet for i år, hvor n = 0 svarer til februar, da de gik på børsen. Dette giver P_0= 45 tusinde. Oktober er 8 måneder senere, så P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ eller }3.66%
Den generelle eksplicitte ligning er P_n =(1.0366)^{n}45. Hvis man forudsiger 24 måneder efter, at de blev offentliggjort, giver det P_{24}=(1,0366)^{24}45=106,63 tusinde brugere.

Eksempel

Hvis vi kigger tilbage på det sidste eksempel, hvad ville CO2-emissionerne så være i 2050 for sammenligningens skyld, hvis emissionerne vokser lineært med samme hastighed?

Vis løsning

Igen vil vi få n = 0 svarende til 1990, hvilket giver P0 = 962. For at finde d kan vi anvende samme fremgangsmåde som tidligere, idet vi noterer os, at emissionerne er steget med 220 mio. tons på 10 år, hvilket giver en fælles forskel på 22 mio. tons hvert år.

Alternativt kan vi anvende en fremgangsmåde svarende til den, vi anvendte til at finde den eksponentielle ligning. Når n = 10, ser den eksplicitte lineære ligning således ud:

P10 = P0 + 10d

Vi kender værdien for P0, så vi kan sætte den ind i ligningen:

P10 = 962 + 10d

Da vi ved, at P10 = 1182, får vi ved at indsætte den ligning

1182 = 962 + 10d

Vi kan nu løse denne ligning for den fælles forskel, d.

1182 – 962 = 10d

220 = 10d

d = 22

Dette fortæller os, at hvis emissionerne ændrer sig lineært, vokser de med 22 millioner tons om året. Hvis vi forudsiger emissionerne i 2050,

P60 = 962 + 22(60) = 2282 millioner tons.

Du vil bemærke, at dette tal er betydeligt mindre end forudsigelsen fra den eksponentielle vækstmodel. Hvis du beregner og plotter flere værdier, kan du illustrere forskellene.

En demonstration af dette eksempel kan ses i følgende video.

Så hvordan ved vi, hvilken vækstmodel vi skal bruge, når vi arbejder med data? Der er to fremgangsmåder, som bør anvendes sammen, når det er muligt:

  1. Find mere end to stykker data. Plot værdierne, og kig efter en tendens. Ser dataene ud til at ændre sig som en linje, eller ser værdierne ud til at kurve opad?
  3. Opmærksom på de faktorer, der bidrager til dataene. Er det ting, du ville forvente, at de ændrer sig lineært eller eksponentielt? I tilfældet med kulstofemissioner kunne vi f.eks. forvente, at de, hvis der ikke er andre faktorer, ville være tæt knyttet til befolkningsværdierne, som har tendens til at ændre sig eksponentielt.

By: adminPosted on

Skriv et svar

Din e-mailadresse vil ikke blive publiceret.