Topologické třídění směrovaných acyklických grafů

Úvod

Směrovaný acyklický graf (DAG) je v informatice směrovaný graf bez cyklů. V tomto kurzu si ukážeme, jak provést topologické třídění na DAG v lineárním čase.

Topologické třídění

V mnoha aplikacích používáme směrované acyklické grafy k označení přednosti mezi událostmi. Například v problému plánování existuje množina úloh a množina omezení určující pořadí těchto úloh. K reprezentaci úloh můžeme sestrojit DAG. Směrované hrany DAG představují pořadí úloh.

Uvažujme problém s tím, jak se může člověk obléknout na slavnostní příležitost. Potřebujeme si obléci několik oděvů, například ponožky, kalhoty, boty atd. Některé oděvy je třeba obléci dříve než ostatní. Například ponožky si musíme obléci dříve než boty. Některé oděvy si můžeme obléci v libovolném pořadí, např. ponožky a kalhoty. Pro ilustraci tohoto problému můžeme použít DAG:

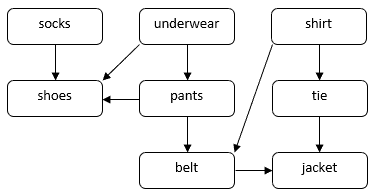
V této DAG vrcholy odpovídají oděvům. Přímá hrana v DAG naznačuje, že si musíme obléci oděv před oděvem . Naším úkolem je najít pořadí oblékání všech oděvů při respektování omezení závislosti. Oděvy můžeme oblékat například v následujícím pořadí:

Topologické uspořádání DAG je lineární uspořádání všech jejích vrcholů tak, že pokud obsahuje hranu , pak se v uspořádání objeví před . Pro DAG můžeme sestrojit topologické třídění s dobou běhu lineární k počtu vrcholů plus počtu hran, což je .

Kahnův algoritmus

V DAG má každá cesta mezi dvěma vrcholy konečnou délku, protože graf neobsahuje cyklus. Nechť je nejdelší cesta z (zdrojový vrchol) do (cílový vrchol). Protože je nejdelší cesta, nemůže existovat žádná příchozí hrana do . DAG tedy obsahuje alespoň jeden vrchol, který nemá žádnou příchozí hranu.

3.1. DAG obsahuje alespoň jeden vrchol, který nemá žádnou příchozí hranu. Kahnův algoritmus

V Kahnově algoritmu sestrojíme topologické třídění na DAG tak, že najdeme vrcholy, které nemají žádnou příchozí hranu:

V tomto algoritmu nejprve vypočítáme hodnoty in-stupňů pro všechny vrcholy.

Poté začneme vrcholem, jehož in-stupeň je 0, a umístíme jej na konec výstupního seznamu. Jakmile vybereme vrchol, aktualizujeme hodnoty in-stupně jeho sousedních vrcholů, protože vrchol a jeho výstupní hrany jsou z grafu odstraněny.

Výše uvedený postup můžeme opakovat, dokud nevybereme všechny vrcholy. Výstupním seznamem je pak topologické třídění grafu.

3.2. Časová složitost

Pro výpočet in-stupňů všech vrcholů musíme navštívit všechny vrcholy a hrany . Proto je doba běhu pro výpočet in-stupňů. Abychom se vyhnuli opětovnému výpočtu těchto hodnot, můžeme použít pole pro sledování hodnot in-stupňů těchto vrcholů. Uvnitř cyklu while musíme také navštívit všechny vrcholy a hrany. Proto je celkový čas běhu .

Hloubkové vyhledávání

K sestavení topologického třídění můžeme také použít algoritmus hloubkového vyhledávání (DFS).

4.1. DFS grafu s rekurzí

Než se budeme zabývat aspektem topologického třídění pomocí DFS, začneme přehledem standardního rekurzivního algoritmu procházení grafu DFS:

Ve standardním algoritmu DFS začneme s náhodným vrcholem v a označíme tento vrchol jako navštívený. Poté rekurzivně zavoláme funkci dfsRecursive, abychom navštívili všechny jeho nenavštívené sousední vrcholy. Tímto způsobem můžeme navštívit všechny vrcholy v čase .

Jelikož však každý vrchol zařazujeme do seznamu ihned při jeho návštěvě a jelikož můžeme začít v libovolném vrcholu, standardní algoritmus DFS nemůže zaručit vygenerování topologicky setříděného seznamu.

Podívejme se, co musíme udělat, abychom tento nedostatek odstranili.

4.2. Způsoby, jakými lze tento nedostatek odstranit. Algoritmus topologického třídění založený na DFS

Můžeme upravit algoritmus DFS tak, aby generoval topologické třídění DAG. Během procházení DFS po návštěvě všech sousedů vrcholu jej pak umístíme na začátek seznamu výsledků . Tímto způsobem můžeme zajistit, že se objeví před všemi svými sousedy v setříděném seznamu:

Tento algoritmus je podobný standardnímu algoritmu DFS. Přestože stále začínáme s náhodným vrcholem, nezařazujeme vrchol do seznamu ihned po jeho návštěvě. Místo toho nejprve rekurzivně navštívíme všechny jeho sousedy a poté vrchol umístíme na začátek seznamu. Pokud tedy obsahuje hranu , pak se objeví v seznamu před .

Celkový čas běhu je také , protože má stejnou časovou složitost jako algoritmus DFS.

Závěr

V tomto článku jsme si ukázali příklad topologického třídění na DAG. Také jsme probrali dva algoritmy, které mohou provést topologické třídění v času.

Implementace topologického třídicího algoritmu založeného na DFS v jazyce Java je k dispozici v našem článku Depth First Search in Java.