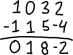Zpět na rejstřík lekcí | Provádět lekce v pořadí | Stránka pro tisk
Operace s řádky matice (strana 1 z 2)
„Operace“ je matematický výraz pro „postupy“. Čtyři „základní operace“ s čísly jsou sčítání, odčítání, násobení a dělení. Pro matice existují tři základní řádkové operace; to znamená, že existují tři postupy, které můžete provádět s řádky matice.
První operací je přepínání řádků. Například při zadání matice:

….můžete prohodit řádky, aby matice měla hezčí řádkové uspořádání, například takto:
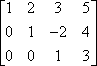
Přehození řádků se často označuje nakreslením šipek, například takto:

Při přehození řádků dávejte pozor na správné kopírování položek.
Druhou operací je násobení řádků. Například při následující matici:

….můžete první řádek vynásobit -1, abyste získali kladnou počáteční hodnotu v prvním řádku:
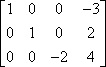
Toto řádkové násobení se často označuje pomocí šipky s násobením uvedeným nahoře, například takto:
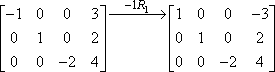
„-1R1“ označuje skutečnou operaci. „-1“ říká, že jsme násobili zápornou jedničkou; „R1“ říká, že jsme pracovali s prvním řádkem. Všimněte si, že druhý a třetí řádek byly beze změny zkopírovány dolů do druhé matice. Násobení se týkalo pouze prvního řádku, takže záznamy pro další dva řádky byly pouze přeneseny beze změny.
Můžete násobit čímkoli chcete. Chcete-li například získat vedoucí jedničku ve třetím řádku předchozí matice, můžete třetí řádek vynásobit zápornou polovinou:

Protože jste s prvním a druhým řádkem nic nedělali, byly tyto záznamy jen beze změny překopírovány do nové matice.
V rámci jednoho kroku můžete provést více než jedno násobení řádků, takže jste mohli oba výše uvedené kroky provést pouze v jednom kroku, například takto:
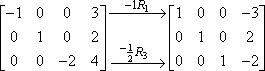
Je dobré používat nějakou formu zápisu (například výše uvedené šipky a indexy), abyste měli přehled o své práci. Matice jsou velmi nepřehledné, zejména pokud je děláte ručně, a poznámky vám mohou usnadnit pozdější kontrolu vaší práce. Udělá to také dojem na učitele.
Poslední řádkovou operací je řádkové sčítání. Řádkové sčítání je podobné metodě „sčítání“ při řešení soustav lineárních rovnic. Předpokládejme, že máte následující soustavu rovnic:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Reklama
Tuto soustavu můžete začít řešit tak, že sečtete sloupce a získáte 4y = 4. Po sečtení sloupců získáte 4y = 4. Po sečtení sloupců získáte 4y = 4:
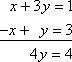
Něco podobného můžete udělat s maticemi.Například při následující matici:

… můžete „zmenšit“ (získat více počátečních nul) druhý řádek tak, že k němu přičtete první řádek (obecným cílem u matic v této fázi je získat „1“ – nebo „0“ a pak „1“ – na začátku každého řádku matice). Když jste redukovali lineární soustavu o dvou rovnicích sčítáním, nakreslili jste přes spodní část „rovnítko“ a sčítali jste dolů. Když používáte sčítání na matici, musíte si vzít nějaký stírací papír, protože se nechcete pokoušet dělat práci uvnitř matice. Sečti si tedy na stírací papír tyto dva řádky:
|
Práce na stíracím papíře – |
|
Toto je tvůj nový druhý řádek; zapíšeš ho na místo starého druhého řádku. Výsledek bude vypadat takto:
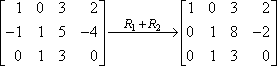
V tomto případě „R1 + R2“ na šipce znamená „přidal jsem první řádek k druhému a toto je výsledek, který jsem dostal“. Protože se řádek jedna ve skutečnosti nezměnil a protože jsme s řádkem tři nic nedělali, zkopírují se tyto řádky do nové matice beze změny.
Top | 1 | 2 | Return to Index Next >>
|
Citujte tento článek jako: |
Stapel, Elizabeth. „Operace s maticovými řadami.“ Purplemath. Dostupné z 2016
|
.