Klasifikace pomocí diskriminační analýzy
Podívejme se, jak lze LDA odvodit jako metodu klasifikace pod dohledem. Uvažujme obecný klasifikační problém: Náhodná proměnná X pochází z jedné z K tříd s určitou hustotou pravděpodobnosti f(x) specifickou pro danou třídu. Diskriminační pravidlo se snaží rozdělit datový prostor na K nesouvislých oblastí, které představují všechny třídy (představte si políčka na šachovnici). S těmito regiony klasifikace pomocí diskriminační analýzy jednoduše znamená, že přiřadíme x do třídy j, pokud se x nachází v regionu j. Otázkou tedy je, jak poznáme, do kterého regionu data x spadají? Přirozeně můžeme postupovat podle dvou alokačních pravidel:
- Pravidlo maximální pravděpodobnosti: Předpokládáme-li, že každá třída se může vyskytovat se stejnou pravděpodobností, pak přiřadíme x do třídy j, jestliže

- Bayesovo pravidlo: Pokud známe prioritu pravděpodobnosti třídy, π, pak přiřadíme x do třídy j, pokud

Lineární a kvadratická diskriminační analýza
Předpokládáme-li, že data pocházejí z vícerozměrného Gaussova rozdělení, tj.tj. rozdělení X lze charakterizovat jeho střední hodnotou (μ) a kovariancí (Σ), lze získat explicitní formy výše uvedených alokačních pravidel. Podle Bayesova pravidla zařadíme data x do třídy j, jestliže má nejvyšší pravděpodobnost ze všech tříd K pro i = 1,…,K:

Výše uvedená funkce se nazývá diskriminační funkce. Všimněte si, že je zde použita logaritmická pravděpodobnost. Jinými slovy nám diskriminační funkce říká, jak pravděpodobná jsou data x z jednotlivých tříd. Rozhodovací hranicí oddělující libovolné dvě třídy, k a l, je tedy množina x, kde mají dvě diskriminační funkce stejnou hodnotu. Jakákoli data, která spadají na rozhodovací hranici, jsou tedy stejně pravděpodobná z obou tříd (nemohli jsme se rozhodnout).
LDA vzniká v případě, kdy předpokládáme stejnou kovarianci mezi třídami K. V případě, že předpokládáme stejnou kovarianci mezi třídami K, vzniká v případě, že předpokládáme stejnou kovarianci. To znamená, že místo jedné kovarianční matice pro každou třídu mají všechny třídy stejnou kovarianční matici. Pak můžeme získat následující diskriminační funkci:

Všimněte si, že se jedná o lineární funkci v x. Rozhodovací hranice mezi libovolnou dvojicí tříd je tedy také lineární funkcí v x, což je důvod jejího názvu: lineární diskriminační analýza. Bez předpokladu stejné kovariance se kvadratický člen v pravděpodobnosti neruší, proto je výsledná diskriminační funkce kvadratickou funkcí v x:

V tomto případě je rozhodovací hranice kvadratická v x. Tento postup se označuje jako kvadratická diskriminační analýza (QDA).
Který postup je lepší? LDA nebo QDA?
V reálných problémech jsou parametry populace obvykle neznámé a odhadují se z trénovacích dat jako výběrové střední hodnoty a výběrové kovarianční matice. QDA sice ve srovnání s LDA umožňuje flexibilnější rozhodovací hranice, ale počet parametrů, které je třeba odhadnout, se také zvyšuje rychleji než u LDA. V případě LDA je ke konstrukci diskriminační funkce v (2) zapotřebí (p+1) parametrů. Pro problém s K třídami bychom potřebovali pouze (K-1) takových diskriminačních funkcí, kdybychom libovolně vybrali jednu třídu jako základní třídu (odečetli bychom pravděpodobnost základní třídy od všech ostatních tříd). Celkový počet odhadovaných parametrů pro LDA je tedy (K-1)(p+1).
Na druhé straně je třeba pro každou diskriminační funkci QDA v (3) odhadnout střední vektor, kovarianční matici a prioritu třídy:
– Střední hodnota: p
– Kovariance: p(p+1)/2
– Priorita třídy: 1
Podobně pro QDA musíme odhadnout (K-1){p(p+3)/2+1} parametrů.
Počet odhadovaných parametrů u LDA tedy roste lineárně s p, zatímco u QDA roste kvadraticky s p. Očekávali bychom, že QDA bude mít při velké dimenzi problému horší výkon než LDA.
Nejlepší ze dvou světů? Kompromis mezi LDA & QDA
Kompromis mezi LDA a QDA můžeme najít regularizací kovariančních matic jednotlivých tříd. Regularizace znamená, že na odhadované parametry klademe určité omezení. V tomto případě požadujeme, aby se individuální kovarianční matice smršťovala směrem ke společné sdružené kovarianční matici prostřednictvím penalizačního parametru, např. α:

Společnou kovarianční matici lze také regularizovat směrem k identické matici prostřednictvím penalizačního parametru, např, β:

V situacích, kdy počet vstupních proměnných výrazně převyšuje počet vzorků, může být kovarianční matice špatně odhadnutelná. Smršťování snad může zlepšit přesnost odhadu a klasifikace. To ilustruje následující obrázek.

Výpočet pro LDA
Z (2) a (3) vidíme, že výpočty diskriminačních funkcí lze zjednodušit, pokud nejprve diagonalizujeme kovarianční matice. To znamená, že data jsou transformována tak, aby měla identickou kovarianční matici (žádná korelace, rozptyl 1). V případě LDA postupujeme při výpočtu takto:

Krok 2 sféruje data tak, aby vznikla identická kovarianční matice v transformovaném prostoru. Krok 4 získáme podle (2).
Podívejme se na příklad dvou tříd, abychom viděli, co LDA skutečně dělá. Předpokládejme, že existují dvě třídy, k a l. Třídu x zařadíme do třídy k, jestliže

Výše uvedená podmínka znamená, že třída k produkuje data x s větší pravděpodobností než třída l. Podle výše uvedených čtyř kroků zapisujeme
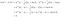
To znamená, klasifikujeme data x do třídy k, jestliže

Vyvozené alokační pravidlo odhaluje fungování LDA. Levá strana (l.h.s.) rovnice je délka ortogonálního průmětu x* na úsečku spojující oba třídní průměty. Pravá strana je poloha středu úsečky korigovaná podle třídních prioritních pravděpodobností. LDA v podstatě klasifikuje sférická data k nejbližšímu průměru třídy. Můžeme zde učinit dvě pozorování:
- Rozhodovací bod se odchyluje od středového bodu, pokud nejsou apriorní pravděpodobnosti tříd stejné, tj. hranice je posunuta směrem ke třídě s menší apriorní pravděpodobností.
- Data se promítají do prostoru, který pokrývají průměry tříd (násobení x* a odečítání průměru na l.h.s. pravidla). Porovnání vzdáleností se pak provádí v tomto prostoru.
.