- Konektivita je základní pojem teorie grafů. Definuje, zda je graf spojitý nebo nespojitý. Bez konektivity není možné projít grafem z jednoho vrcholu do jiného vrcholu.
- O grafu se říká, že je spojitý, jestliže mezi každou dvojicí vrcholů existuje cesta. Z každého vrcholu do každého jiného vrcholu musí existovat nějaká cesta, kterou lze projít. Tomu se říká konektivita grafu.
- O grafu se říká, že je nespojitý, jestliže existuje více nespojitých vrcholů a hran.
- Teorie konektivity grafu je nezbytná v síťových aplikacích, při směrování dopravních sítí, při toleranci sítí atd.
Příklad
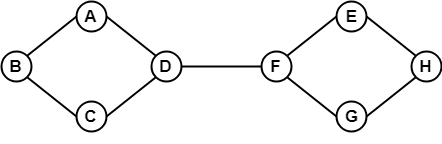
V uvedeném příkladu je možné cestovat z jednoho vrcholu do jiného vrcholu. Zde můžeme cestovat z vrcholu B do H pomocí cesty B -> A -> D -> F -> E -> H. Jedná se tedy o spojitý graf.
Příklad
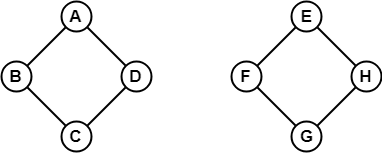
Ve výše uvedeném příkladu není možné cestovat z vrcholu B do H, protože mezi nimi neexistuje žádná cesta přímo ani nepřímo. Jedná se tedy o nespojitý graf.
Podívejme se na některé základní pojmy spojitosti.
Vrchol řezu
Jediný vrchol, jehož odstraněním se graf rozpojí, se nazývá vrchol řezu.
Nechť G je spojitý graf. Vrchol v z G se nazývá řezaný vrchol G, jestliže výsledkem G-v (Odstranit v z G) je nespojitý graf.
Pokud z grafu odstraníme vrchol, pak se graf rozpadne na dva nebo více grafů. Tento vrchol se nazývá řezaný vrchol.
Poznámka: Nechť G je graf s n vrcholy:
- Spojitý graf G může mít maximálně (n-2) řezaných vrcholů.
- Odstraněním řezaného vrcholu může graf zůstat nespojitý.
- Odstraněním vrcholu se může zvýšit počet komponent grafu alespoň o jednu.
- Každý nepřevislý vrchol stromu je řezaným vrcholem.
Příklad 1

Příklad 2
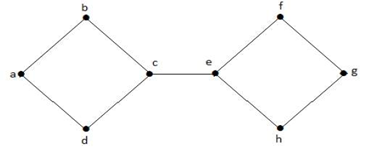
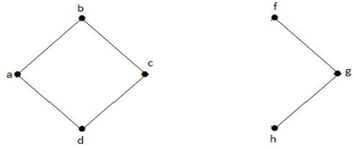
V uvedeném grafu je vrchol ‚e‘ řezaným vrcholem. Po odstranění vrcholu ‚e‘ z výše uvedeného grafu se graf stane nespojitým grafem.
Řezná hrana (most)
Řezná hrana neboli most je jediná hrana, jejímž odstraněním se graf rozpojí.
Nechť G je spojitý graf. Hrana e z G se nazývá řezaná hrana G, jestliže výsledkem G-e (Odstranění e z G) je nespojitý graf.
Pokud z grafu odstraníme hranu, pak se graf rozpadne na dva nebo více grafů. Tato odstraněná hrana se nazývá řezná hrana nebo můstek.
Poznámka: Nechť G je graf s n vrcholy:
- Spojitý graf G může mít nejvýše (n-1) řezných hran.
- Odstraněním řezné hrany může graf zůstat nespojitý.
- Odstranění hrany může zvýšit počet komponent grafu nejvýše o jednu.
- Řezná hrana „e“ nesmí být součástí žádného cyklu v grafu G.
- Pokud existuje řezná hrana, pak musí existovat i řezný vrchol, protože alespoň jeden vrchol řezné hrany je řezným vrcholem.
- Pokud existuje řezaný vrchol, pak není nutná existence žádné řezané hrany.
Příklad 1
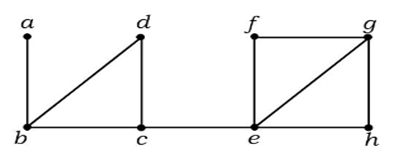
V uvedeném grafu je hrana (c, e) řezanou hranou. Po odstranění této hrany z výše uvedeného grafu se graf stane nespojitým grafem.
Příklad 2
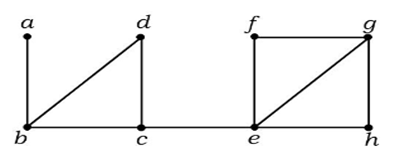
Ve výše uvedeném grafu je hrana (c, e) řezaná hrana. Po odstranění této hrany z výše uvedeného grafu se graf stane nespojitým grafem.
Řezná množina
Ve spojitém grafu G je řezná množina množina S hran s následujícími vlastnostmi:
- Odstraněním všech hran v S se G rozpojí.
- Odstranění některých hran (ale ne všech) v S nerozpojí G.
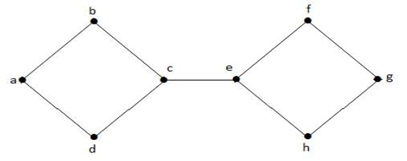
Příklad 1
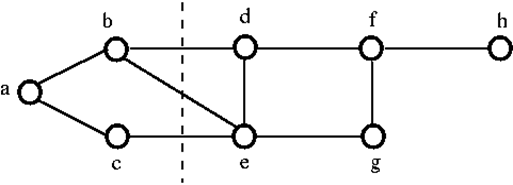
Chceme-li výše uvedený graf G rozpojit, musíme odstranit tři hrany, tj. bd, be a ce. Nemůžeme jej rozpojit odstraněním pouze dvou ze tří hran. Proto je {bd, be, ce} řezaná množina.
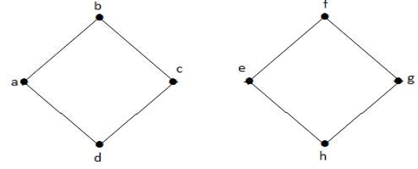
Po odstranění řezané množiny z výše uvedeného grafu by vypadal takto:
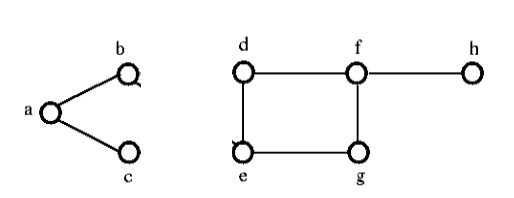
Spojitost hran
Spojitost hran spojitého grafu G je minimální počet hran, jejichž odstraněním je graf G nespojitý. Označuje se λ(G).
Když je λ(G) ≥ k, pak se říká, že graf G je k-hranově propojený.
Příklad
Podívejme se na příklad,
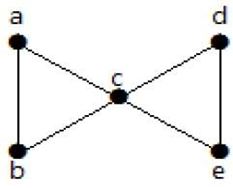
Z výše uvedeného grafu se odstraněním dvou minimálních hran stane spojitý graf nespojitým. Jeho hranová spojitost je tedy 2. Výše uvedený graf je tedy grafem spojeným dvěma hranami.
Zde jsou uvedeny následující čtyři způsoby rozpojení grafu odstraněním dvou hran:
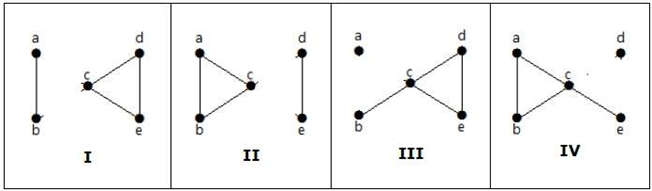
Vertex Connectivity
Spojitost (neboli vrcholová spojitost) spojeného grafu G je minimální počet vrcholů, jejichž odstraněním se G rozpojí nebo zredukuje na triviální graf. Označuje se K(G).
Říká se, že graf je k-spojený nebo k-vrcholově spojený, když K(G) ≥ k. Abychom odstranili vrchol, musíme odstranit i hrany, které s ním incidentují.
Příklad
Podívejme se na příklad:
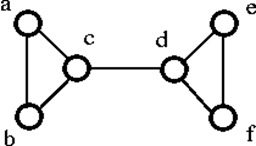
Výše uvedený graf G lze rozpojit odstraněním jediného vrcholu buď „c“, nebo „d“. Jeho vrcholová konektivita je tedy 1. Jedná se tedy o graf s 1 konektivitou.
.